Coğrafi Bilgi Sistemleri İçin Temel Matematik Ara 6. Deneme Sınavı
Toplam 14 Soru1.Soru
Bir dersi alan 100 kişiden geçen ve kalan kişiler ile bu kişilerin cinsiyetleri aşağıda verilmiştir. Dersten geçen erkeklerin sayısı 49, kadınların sayısı 21 dir. Dersten kalan erkeklerin sayısı 21, kadınların sayısı 9 dur. Buna göre bu dersten geçenlerin cinsiyetinin kadın olma olasılığı hangi seçenekte doğru olarak verilmiştir?
|
0.1 |
|
0.2 |
|
0.3 |
|
0.4 |
|
0.5 |
Dersi alan 100 kişiden kalan kişi sayısı 30 geçen kişi sayısı ile 70 olarak verilmiştir. Bu dersi geçenlerden 21 i kadın ve 49 u erkek olarak verildiğine göre bileşen olasılığa göre dersi geçen kişilerin kadın olma olasılığı:
P(K) = 21 / (21 + 49)
P(K) = 21/70
P(K) = 0.3 olarak bulunur. Doğru cevap C seçeneğinde verilmiştir.
2.Soru
ise f(2)+f(-1) kaçtır?
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
Fonksiyon
x≥1 iken 3x+4,
x˂1 iken x2+2x değerine eşittir.
O halde x=2 için f(2)=3.2+4=10 ve f(-1)=(-1)2+2.(-1)=-1 olur. O halde
f(2)+f(-1)=9 bulunur.
3.Soru
fonksiyonun tanım kümesi aşağıdakilerden hangisidir?
|
[2,∞) |
|
(-∞,2) |
|
(2,∞) |
|
(-∞,2] |
|
(-2,2) |
Payda sıfır olmayacağından ve köklü ifadenin içi de negatif olamayacağından 2-x>0 olmalıdır. Buradan x<2 olur. Bu durumda f fonksiyonunun tanım kümesi Df=(-∞,2) olur.
4.Soru
a vektörünün uzunluğu ve b vektörünün uzunluğu
olsun. a⋅b iç çarpımının değeri 3 olduğuna göre iki vektör arasındaki açı aşağıdakilerden hangisidir?
|
30o |
|
45o |
|
60o |
|
90o |
|
135o |
olduğu için iki vektör arasındaki açı 45° dir.
5.Soru
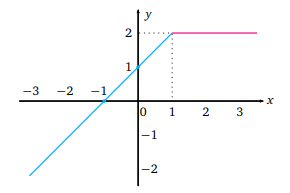 grafiği verilen fonksiyon aşağıdakilerden hangisidir?
grafiği verilen fonksiyon aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
|
verilen fonksiyonun grafiğinden
iken y=f(x)=2 olduğu görülmektedir. x<1 iken ise fonksiyon (-1, 0) ve (0, 1) noktalarından geçmektedir. Bu noktalardan geçen fonksiyon;
eşitliği yardımıyla bulunabilir. İlgili değerler yerine konulduğunda fonksiyon x<1 iken
olarak elde edilir. Dolayısıyla Doğru Cevap E seçeneği olur.
6.Soru
|
-1 |
|
2 |
|
5 |
|
7 |
|
11 |
Verilen fonksiyonlara göre olarak bulunmaktadır.
7.Soru
f(x)= (4x+2)/(2x-1) ve g(x)= 2x+1 fonksiyonları için fog(x) fonksiyonu nedir ?
|
(8x-2)/(4x+1) |
|
(x-2)/(x+1) |
|
(8x+2)/(3x+1) |
|
(6x+3)/(4x-1) |
|
(x-2)/4x |
fog(x)=f(g(x)) olduğu için
f(g(x)) = (4(2x-1)+2)/(2(2x+1)-1) = (8x-4+2)/(4x+2-1) = (8x-2)/(4x+1) olarak bulunur.
8.Soru
Deneyin içinde birden fazla değişken ve kişi ortam veya koşullara bağlı değişimlerin söz konusu olduğu olasılık tanımlaması aşağıdakilerden hangisidir?
|
Öznel |
|
Klasik |
|
Sayma |
|
Göreli sıklık |
|
Bileşen |
Deneyin içinde birden fazla değişken ve kişi ortam veya koşullara bağlı değişimlerin söz konusu olduğu durumlarda öngörülen olasılığı öznel olasılık denilmektedir.
9.Soru
Olayın mümkün olan tüm sonuçlarının olasılıklarını ifade eden matematiksel model olarak tanımlanan kavram aşağıdakilerden hangisidir?
|
Değişken |
|
Rassal değişken |
|
Kesikli model |
|
Kesikli değişken |
|
Olasılık dağılımı |
Olasılık dağılımı, olayın mümkün olan tüm sonuçlarının olasılıklarını ifade eden matematiksel model olarak tanımlanabilir. Olasılık dağılım modelleri rassal değişkenin tipine göre farklılık göstermektedir.
10.Soru
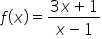 olmak üzere
olmak üzere 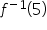 ifadesinin eşiti aşağıdakilerden hangisidir?
ifadesinin eşiti aşağıdakilerden hangisidir?
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
biçimindeki fonksiyonun tersi;
olarak bulunur.
biçiminde verildiğinde fonksiyonun tersi;
olarak elde edilir. Soruda istenen
olduğundan
sonucuna ulaşılır. Bu nedenle Doğru Cevap C seçeneği olur.
11.Soru
ifadesi aşağıdakilerden hangisine eşittir ?
|
|
|
|
|
0,1 |
|
1 |
|
2 |
12.Soru
30 erkek, 20 kız öğrenciden oluşan bir sınıfta 12 kız öğrenci ve 18 erkek öğrenci gözlük kullanmaktadır. Rastgele seçilen bir öğrencinin kız olduğu biliniyor ise gözlüklü olmama olasılığı nedir?
|
2/5 |
|
3/5 |
|
4/5 |
|
2/3 |
|
6/7 |
Rastgele seçilen bir öğrencinin kız olduğu biliniyor ise 20 kız öğrenci olup bunun 12 si gözlük kullandığı için 8 i gözlük kullanmıyordur. Böylece istenilen olasılık 8/20=2/5 bulunur.
14.Soru
şeklindeki matrisler verilsin.
Bu duruma matrisi aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
|
Verilen matrisleri çarptığımızda,


