Coğrafi Bilgi Sistemleri İçin Temel Matematik Ara 8. Deneme Sınavı

Toplam 18 Soru

Diğer "Coğrafi Bilgi Sistemleri İçin Temel Matematik" Sınavları

PAYLAŞ:

1.Soru

ise A matrisinin determinantı aşağıdakilerden hangisidir?

-4

-2

0

2

4

2.Soru

eşitsizliğini sağlayan x tamsayılarının toplamı aşağıdakilerden hangisidir?

2

3

4

6

8

3.Soru

f(x)= x + 1 ise f^-1(7) kaçtır ?

2

4

6

8

10

4.Soru

Bir otobüste yolculardan 30 tanesi erkek, 10 tanesi bayandır. Erkeklerden 10 tanesi, bayanlardan 5 tanesi kahverengi gözlüdür. Gelişigüzel seçilen yolcunun erkek veya kahverengi gözlü ola olasılığı aşağıdakilerden hangisidir?

20/30

25/30

35/40

30/40

25/40

5.Soru

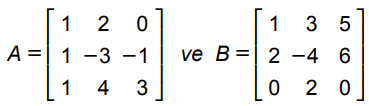matrisleri veriliyor. C = A.B eşitliği verildiğine göre C matrisinin 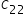elemanı aşağıdakilerden hangisidir?

11

12

13

14

15

6.Soru

ve ise ise x kaçtır ?

-1

0

1

2

3

7.Soru

A matrisinin boyutu 3x4 , B matrisinin boyutu 4x2 ce C matrisinin boyutu 2x3 olsun. (A.B.C)T işleminin sonucu çıkan matrisin boyutu ne olur ?

2x2

2x3

3x3

3x4

4x3

8.Soru

Bir otomobil bayisinin günlük araba satış sayısına bağlı olasılık dağılımı aşağıdaki gibidir:Bir otomobil bayisinin günlük araba satış sayısına bağlı olasılık dağılımı aşağıdaki gibidir:

Bu dağılışa göre bayinin 100 günde beklediği satış değeri kaç olmalıdır?

189

224

261

292

371

9.Soru

f(x) = x² + 1 fonksiyonunun görüntü kümesi aşağıdakilerden hangisidir?

10.Soru

Bir torbada 7 tane sarı 3 tane mavi ve 8 tane kırmızı bilye vardır. Ali bu torbadan bir bilye çekiyor. Çekilen bilyenin mavi olma olasılığı kaçtır?

1/5

4/9

2/9

1/6

7/8

11.Soru

ise secx=?

12.Soru

|x-1|<2 eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir?

(4,7)

[-4,-1]

(-1,3)

(2,7)

(3,4)

13.Soru

A(2,-1), B(-1,y), C(1,3) noktalarının doğrusal olması için y ne olmalıdır?

-8

-11

6

11

-6

14.Soru

Birbirinden farklı üç basamaklı üç pozitif tam sayının toplamı 432’ dir. Bu sayıların en büyüğü en fazla kaçtır?

201

211

221

231

241

15.Soru

Bir olayın olma olasılığı aşağıdakilerden hangisi olabilir?

2

3/2

4/3

5/4

5/6

16.Soru

vektörlerinin a×b dış çarpımının sonucu aşağıdakilerden hangisidir?

-3i+j+10k

3i-j-10k

-3i-j-10k

2i-12j

2i-12k

17.Soru

Bir kümenin tüm altkümelerinin sayısı 64 olduğuna göre bu kümenin eleman sayısı kaçtır?

7

6

5

4

3

18.Soru

|¦(3&-1&0@2&5&4@7&0&-3)| matrisinin determinantı kaçtır ?

23

35

-12

-79

41