Coğrafi Bilgi Sistemleri İçin Temel Matematik Final 18. Deneme Sınavı
Toplam 16 Soru1.Soru
f(x) = x2 + x ve olmak üzere
ise a kaçtır ?
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
olur.
Buradan
olarak bulunur.
2.Soru
Üç üyelik fonksiyonunun bulanıklaştırma değerleri verildiğinde durulaştırma sonucu aşağıdakilerden hangisi olabilir?
|
Üyelik fonksiyonlarının birleşiminden elde edilen geometrik şeklin yükseklik metoduna göre elde edilen değer |
|
İkinci üyelik fonksiyonunun minimum seçecek şekilde durulaştırma işleminin yapılması |
|
Üç üyelik fonksiyonunun ağırlık merkezlerinin minimum değere sahip olanı. |
|
Üç üyelik fonksiyonundan en yüksek değere sahip olan üyelik fonksiyonunun ağırlık merkezi |
|
Durulaştırmada üç üyelik fonksiyonuna gelen aktivasyon fonksiyonlarının yükseklik metoduna göre sonucu |
Diğer şıklarda belirtilen hesaplama işlemleri doğru değildir
3.Soru
Aşağıda verilen fonksiyon grafiklerinden hangisi, bulanık mantıkta
kullanılan bir yamuk üyelik fonksiyonu grafiğidir?
|
|
|
|
|
|
|
|
|
|
Sayfa 180 de yamuk üyelik fonksiyonunun genel şekli verilmiştir. Orada verilen formülde
a=1,b=2,c=3 ve d=4 alınırsa E) şıkkındaki grafik elde edilir.
4.Soru
ise A matrisinin determinantı aşağıdakilerden hangisidir?
|
0 |
|
-1 |
|
-6 |
|
-8 |
|
-12 |
biçiminde 3×3 tipinde bir matrisinin determinantı
biçiminde hesaplanır. Bu durumda elde edilir.
5.Soru
A = (-1.1) noktasının kutupsal gösterimi aşağıdaki seçeneklerin hangisinde doğru olarak gösterilmiştir ?
|
[√3 , 〖120〗^0 ] |
|
[-√2 , 〖225〗^0 ] |
|
[-√2 , 〖135〗^0 ] |
|
[√2 , 〖45〗^0 ] |
|
[√2 , 〖135〗^0 ] |
a= r cosϴ
r = √(a^2+b^2 ) = √(〖(-1)〗^2+〖(1)〗^2 ) = √2
ϴ = arctanb/a = arctan1/(-1) = arctan(-1) = 〖135〗^0
Bu durumda A noktasının kutupsal koordinatları [√2 , 〖135〗^0 ]
6.Soru
Yukarıdaki grafikte Çok Soğuk – Soğuk – Ilık – Sıcak – Çok Sıcak kavramlarını temsil eden üyelik fonksiyonları gösterilmiştir.
14C0 sıcaklık için aşağıdakilerden hangisi doğrudur?
|
|
|
|
|
|
|
|
|
|
olur.
7.Soru
Aşağıdaki matrislerden hangisi bir ölçekleme dönüşümünü temsil edebilir.
|
[¦(1&0@0&2)] |
|
[¦(1&0&3@0&-1&1)] |
|
[¦(1&-2@0&2)] |
|
[¦(1&2&3)] |
|
[¦(1&0@0&2@3&0)] |
İki boyutlu uzaydaki bir T(x,y) ölçekleme dönüşümü [¦(x^ı@y^ı )] = [¦(s_x&0@0&s_y )].[¦(x@y)] şeklinde gösterilir.
8.Soru
serisinin limiti hangi seçenekte doğru verilmiştir?
|
5 |
|
10 |
|
15 |
|
20 |
|
25 |
serisinde
olduğundan
doğru cevap B seçeneğinde verilmiştir.
9.Soru
dizisinin limiti aşağıdakilerden hangisidir?
|
0 |
|
-2 |
|
|
|
|
|
∞ |
10.Soru
Aşağıdakilerden hangisi üyelik fonksiyonlarının belirlenmesinde
kullanılan başlıca yöntemlerden biri değildir?
|
Çıkarım |
|
Mertebeleme |
|
Açılı bulanık kümeler |
|
Çıkarımcı muhakeme |
|
Anket çalışmaları |
Anket çalışmaları üyelik fonksiyonlarının belirlenmesinde
kullanılan başlıca yöntemlerden biri değildir
11.Soru
parabolü ile X ekseni arasındaki alan aşağıdakilerden hangisinde doğru olarak verilmiştir?
|
200/5 |
|
125/6 |
|
100/5 |
|
180/6 |
|
75/5 |
12.Soru
Nihat’ın 2 çocuğundan en az birisi kızdır. Buna göre Nihat’ın iki çocuğunun da kız olma olasılığı nedir?
|
|
|
|
|
|
|
|
|
|
İki çocuk için olası tüm durumlar
(Erkek Erkek),(Erkek Kız),(Kız Erkek),(Kız Kız)
olur. Sadece son üç tanesi verilen koşula uymaktadır. Yani örnek uzayımız
S = { (Erkek,Kız),(Kız,Erkek),(Kız,Kız)}
olur. Bunların içinden sadece sonuncusu istenen durumdur. O halde cevap 1/3 olur.
13.Soru
toplamının sonucu aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
∞ |
r = > 1 ve a =1>0 olduğundan seri ∞’a ıraksar.
14.Soru
Bir küpün 8 köşesinden 3’ü beyaza 3’ü kırmızıya 2’si ise siyaha boyanmaktadır. Bu küpte, iki ucu siyaha boyalı bir ayrıt (köşeleri birleştiren doğru parçası) bulunma olasılığı kaçtır?
|
|
|
|
|
|
|
|
|
|
Bir küpte bir köşeye komşu ve bir ayrıt oluşturabilecek 3 köşe bulunmaktadır. Buna göre siyah bir köşeye komşu bir köşenin siyah olma olasılığı
olarak hesaplanmaktadır. Bir başka yolla ise, 8 kenarın oluşturduğu toplam 12 ayrıttan birinin iki kenarının da siyah olma olasılığı
olarak hesaplanabilmektedir.
15.Soru
vektörünün boyu aşağıdakilerden hangisidir?
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
vektörünün boyu
olarak bulunur.
16.Soru
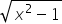fonksiyonunun tanım kümesi aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
|
fonksiyonunun tanım kümesini için karekökün içinin sıfırdan büyük ve eşit olması gerekir. Buradan;
kökün içindeki ifadeyi sıfır yapan değerler -1 ve 1 olarak bulunur. Bulunan bu değerlere göre kökün içindeki ifadenin işaret incelemesi yapılırsa;
elde edilir. Karekökün içinin sıfırdan büyük ve eşit olması istendiğinden fonksiyonun tanım kümesi;
olarak bulunur. Bu ifadenin seçeneklerde yer alan eşiti ise
olup Doğru Cevap E seçeneğidir.