DEVRE ANALİZİ - Ünite 2: Devre Yasaları Özeti :
PAYLAŞ:Ünite 2: Devre Yasaları
Temel Kavramlar
Kapalı bir devrede üzerinden akım geçen tüm elemanlara devre elemanı denir. Şekilde direnç (R), gerilim kaynağı ve iletken birer devre elemanıdır (Gerilim kaynağı ve direncin farklı çizimleri ikinci şekilde gösterilmiştir.)

Bir elektrik devresinde iki ya da daha fazla devre elemanının bağlı olduğu noktaya düğüm veya düğüm noktası denir. Şekilde R 1 , R 2 ve R 4 dirençlerinin birleştiği yer bir düğüm noktasıdır. Genellikle seri bağlı iki elemanın olduğu noktalara düğüm noktası işaretlenmez. Çünkü seri bağlı elemanlardan geçen akım aynıdır. Örneğin şekilde R 2 ve R 3 dirençleri seri bağlıdır ve geçen akım aynı olduğundan bu iki direncin birleştiği yerin düğüm noktası olmasına gerek yoktur.

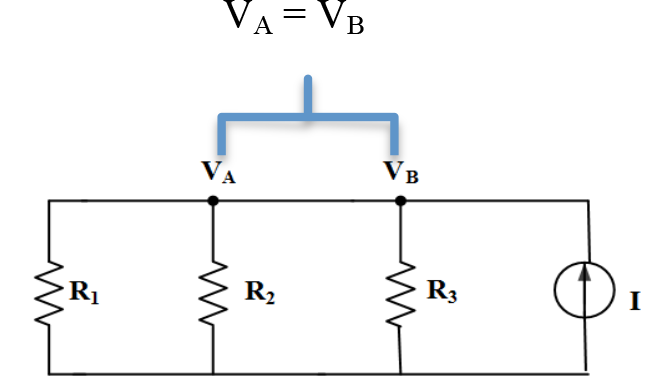
Akım bölümünün gerçekleşeceği üç ya da daha fazla elemanın bağlı olduğu düğüm noktalarına temel düğüm noktası denir. Şekilde V A ve V B birer temel düğüm noktasıdır.

Her bir devre elemanının üzerinde yer aldığı devre parçasına kol denir . Diğer bir tanım: kol , düğüm noktaları arasında kalan ve aynı akımın geçtiği devre parçasıdır. Şekilde B ve E noktaları birer düğüm noktasıdır ve düğüm noktaları arasında kalan aynı akımın geçtiği EFAB, BE ve BCDE birer koldur.
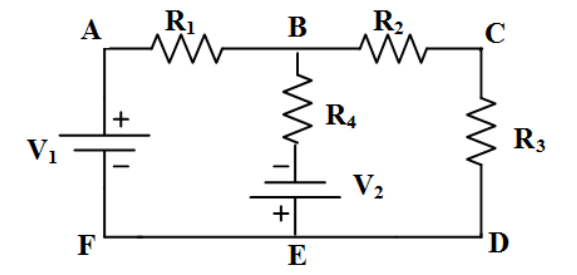
Kolları üzerinde devre elemanları bulunan kapalı devreye çevre denir. Şekilde verilen devrede üç tane çevre bulunmaktadır. V 2 gerilim kaynağı, V 1 gerilim kaynağı, R 1 ve R 4 dirençlerinden oluşan kısım (mavi), V 2 gerilim kaynağı, R 4 , R 2 ve R 3 dirençlerinden oluşan kısım (turuncu), V 1 gerilim kaynağı, R 1 , R 2 ve R 3 dirençlerinden oluşan kısım (yeşil) birer çevredir.
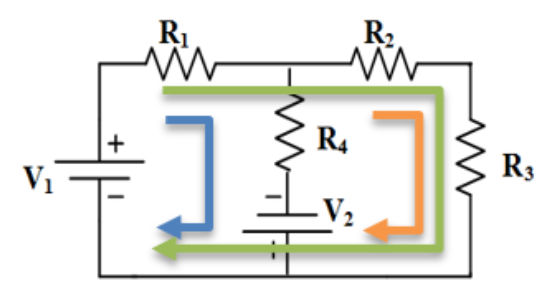
Bir kapalı devrede kollar tarafından kesilmeden oluşturulan en küçük çevreye göz denir. Şekilde, R 1 , R 4 dirençleri, V 2 gerilim kaynağı ve V 1 gerilim kaynağından oluşan kısım (mavi), V 2 gerilim kaynağı, R 4 , R 2 ve R 3 dirençlerinden oluşan kısım (turuncu) birer gözdür. Bu gözler aynı zamanda birer çevredir. Her göz bir çevredir fakat her çevre bir göz değildir. Çünkü göz olabilmesi için içerisinde kol olmaması gerekir. Yukarıdaki şekilde V 1 gerilim kaynağı, R 1 , R 2 ve R 3 dirençlerinden oluşan kısım çevre olarak alınabilmesine rağmen göz değildir. Çünkü içerisinde R 4 direnci ve V 2 gerilim kaynağından oluşan bir kol bulunmaktadır.

Kirchhoff Yasaları
Kirchhoff yasaları, devre çözüm yöntemlerinin ve devre teoremlerinin temelini oluşturmaktadır. Devreden geçen akımı ve devredeki gerilimleri bulmak için kullanılır. Kirchhoff ‘un yasaları, seri, paralel ve karışık devrelerde kullanılan temel yasalardır. Kirchhoff yasaları iki tanedir:
- Gerilim yasası
- Akım yasası
Kirchhoff’un gerilim yasası , kapalı bir elektrik devresinde devreye uygulanan gerilim ile seri bağlı dirençlerin üzerindeki gerilim düşümlerinin toplamının sıfıra eşit olduğunu ifade etmektedir. Bir başka deyişle devredeki dirençlerin üzerindeki gerilim düşümlerinin toplamı devreye uygulanan gerilime eşittir.
Şekil kapalı bir devre olup, devreye uygulanan E gerilim kaynağı ile devreden bir I akımı geçmektedir. Akım ile direnç değeri çarpılarak yani Ohm yasası ile R 1 , R 2 ve R 3 dirençleri üzerindeki gerilim düşümleri hesaplanır:
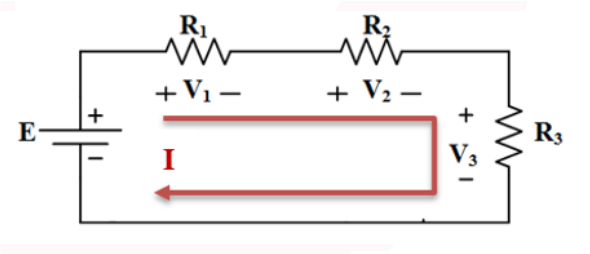
V 1 = I. R 1 ( R 1 direnci üzerindeki gerilim düşümü)
V 2 = I. R 2 ( R 2 direnci üzerindeki gerilim düşümü)
V 3 = I. R 3 ( R 3 direnci üzerindeki gerilim düşümü)
I akımının yönüne (saat yönü) göre gerilim düşümlerinin (+) ve (-) yönleri şekilde gösterildiği gibidir. Daha sonra Kirchhoff’un gerilim yasası devreye uygulanarak denklem oluşturulur. I akımı E gerilim kaynağının önce eksi ucu ile karşılaşmaktadır. Kirchhoff’un gerilim yasasına göre:
–E + V 1 + V 2 + V 3 = 0
yazılır.
Bu eşitlik devreye uygulanan gerilim ile dirençlerin üzerindeki gerilim düşümlerinin toplamının sıfıra eşit olduğunu göstermektedir. E eşitliğinin diğer tarafına alınarak,
E =V 1 + V 2 + V 3
eşitliği oluşturulursa Kirchhoff’un gerilim yasasının diğer ifade şekli elde edilir. Yani devreye uygulanan gerilim, dirençlerin üzerindeki gerilim düşümlerinin toplamına eşittir.
Eğer devrede dolaşan akımın yönüne ters yönde bir akım yönü seçilirse (aşağıdaki şekilde akımın yönü saat yönünde olması gerekirken saat yönünün tersinde seçilmiştir) Kirchhoff’un gerilim yasası yine aynı şekilde uygulanır. Şekilde I akımının yönüne göre dirençlerin üzerindeki gerilim düşümlerinin (+) ve (-) yönleri gösterilmiştir.

I akımı E gerilim kaynağının önce artı ucu ile karşılaşmaktadır. Kirchhoff’un gerilim yasasına göre:
V 3 + V 2 + V 1 + E = 0
yazılır. E eşitliğinin diğer tarafına alınarak,
–E =V 1 + V 2 + V 3 eşitliği elde edilir.
Kirchhoff’un gerilim yasası seri bağlı devrelerin çözümünde kullanılır. Ayrıca devre çözüm yöntemlerinden çevre akımları yönteminin de temelini oluşturmaktadır. Devrede çözüm yapılırken akımın yönü saat yönünde veya saat yönünün tersinde seçilebilir. Çözümü istenen devrede akımın bulunması isteniyorsa ve bulunan akımın değeri negatif ise, bu seçilen akımın yönünün ters olduğunu göstermektedir.
Kirchhoff’un akım yasası bir düğüm noktasına gelen akımların toplamının, bu noktadan giden akımların toplamına eşit olduğunu ifade eder. Bir başka deyişle bir düğüm noktasına gelen akımlarla, düğüm noktasından giden akımlarının toplamı sıfıra eşittir. Düğüm noktasına gelen akımlar eksi (-), düğüm noktasından giden akımlar artı (+) ile gösterilir.
Şekilde öncelikle ikiden fazla ucun birleştiği yere bir düğüm noktası (A) adı verilir. A düğüm noktasında altı tane kol birleşmektedir. Düğüm noktasına I 2 , I 3 , I 4 ve I 6 akımları düğüme gelen akımdır ve bunlar eksi ile gösterilir. I 1 ve I 5 akımları düğümden giden akımdır ve artı ile gösterilir.
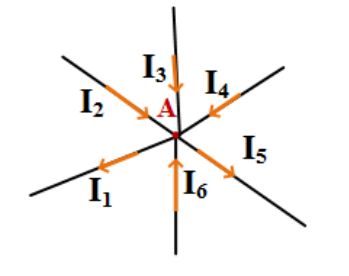
Şekilde altı kolun birleştiği A düğüm noktasına Kirchhoff’un akım yasası uygulanarak denklem oluşturulur.
I 1 – I 2 – I 3 – I 4 + I 5 – I 6 =0
Bu eşitlik düğüm noktasına gelen akımlarla, düğümden giden akımların toplamının sıfıra eşit olduğunu göstermektedir. Düğüme gelen akımlar eşitliğin diğer tarafına alınarak
I 2 + I 3 + I 4 + I 6 = I 1 + I 5
eşitliği oluşturulursa Kirchhoff’un akım yasasının diğer ifade şekli elde edilir. Yani düğüme gelen akımların toplamı, düğümden giden akımların toplamına eşittir.
Kirchhoff’un akım yasası paralel bağlı devrelerde kullanılır. Ayrıca devre çözüm yöntemlerinden düğüm noktası yönteminin de temelini oluşturmaktadır.
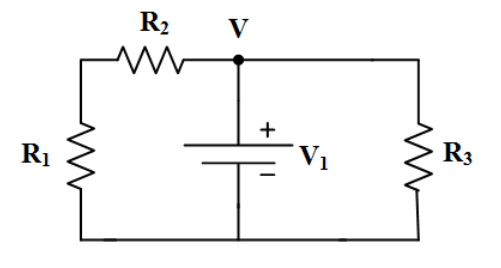
Devrede çözüm yapılırken düğüm noktasının bulunduğu kollardan birinde sadece bir gerilim kaynağı var ise düğüm noktasının gerilim değeri gerilim kaynağının değerine eşittir. Şekilde V düğüm noktasının değeri V 1 gerilim kaynağının değerine eşittir. V = V 1 eşitliği elde edilir.
Eğer iki düğüm noktası arasında direnç yoksa bu iki düğüm noktası aynı düğüm noktasını gösterir. Şekilde iki tane (V A ve V B ) düğüm noktası arasında direnç olmadığı için bu iki düğüm noktası aynı düğüm noktasıdır. Devre tek düğüm noktası olarak çözülerek istenilen değerler bulunur.