ENERJİ ANALİZİ - Ünite 4: Termodinamik ve Enerji Özeti :

PAYLAŞ:

Ünite 4: Termodinamik ve Enerji

Termodinamiğin Birinci Yasası

Termodinamiğin birinci yasası, enerjinin niceliği ile ilgili enerji korunumu yasasıdır . Termodinamiğin birinci yasasını, hem kapalı sistemler hem de kontrol hacimleri için nasıl yazabileceğimizi görerek karşımıza çıkacak herhangi bir sistemin çözümlemesini yapabileceğiz.

Çevrim yapan bir sistem için birinci yasa analitik olarak Q _giren -Q _çıkan =Q _net ve W _çıkan -W _giren =W _net dersek birinci yasayı aşağıdaki şekilde yazarız:

Q _net =W _net

Hal değişimi olan sistem için birinci yasayı analitik olarak aşağıdaki şekilde yazabiliriz (S:74, Şekil 4.2).

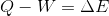
$Q-W=\Delta E$

Burada Q sisteme aktarılan ısıyı, W sistemin yaptığı işi ve 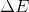$\Delta E$ ise sistemin hal değişimi sırasında enerjisindeki değişimi göstermektedir. Genellikle bir ısı kaynağından yararlanarak iş elde edilmesi önemsendiğinden, birinci yasa aşağıdaki şekilde yazılarak kullanılır:

Q ₁₂ =(E ₂ -E ₁ )+W ₁₂

Sistemin enerjisi (E), iç enerji (U), kinetik enerji (KE) ve potansiyel enerji (PE) şeklinde ayrı ayrı dikkate alınabilir. Hal değişimi yapan bir sistemin birinci yasa analizini yapalım dediğimizde aşağıdaki denklemi kullanırız:

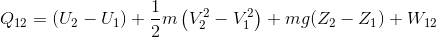
$Q_{12}=(U_{2}-U_{1})+\frac{1}{2}m\left ( V_{2}^{2}-V_{1}^{2} \right )+mg(Z_{2}-Z_{1})+W_{12}$

Kontrol hacmi için kütle korunumu yasası ; kontrol hacmine giren ve çıkan kütleler arasındaki fark kontrol hacmi içindeki kütlenin değişimine eşittir şeklinde söylenir (S:76, Şekil 4.4). Bir kontrol hacmine birden çok yerden kütle giriş ve çıkışı olabileceği düşünülürse kütle korunumu denklemi aşağıdaki şekilde yazılır:

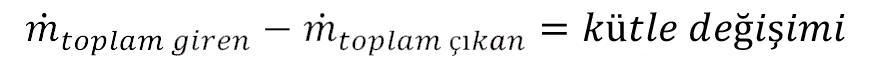
Bir kontrol hacmi için birinci yasa; enerji korunumu açısından bakıldığında bir kontrol hacminin kapalı sistemden farkı yalnızca kütle giriş ve çıkışının olmasıdır. Akış işi PV şeklinde olduğundan, akan akışkanın toplam enerjisi E _f entalpinin tanımından yararlanarak, aşağıdaki şekilde yazabiliriz:

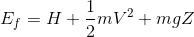
$E_{f}=H+\frac{1}{2}mV^{2}+mgZ$

Kontrol hacmine ısı ve iş geçişi ve kütle akışları nedeniyle enerji giriş (i) ve çıkışının (e) olduğunu düşünerek, enerji korunumu yani kontrol hacmi için birinci yasa ifadesi, aşağıdaki denklem ile verilir:

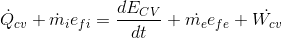
$\dot{Q}_{cv}+\dot{m}_{i}e_{fi}=\frac{dE_{CV}}{dt}+\dot{m_{e}}e_{fe}+\dot{W_{cv}}$

Burada birimin (kJ/s) yani Watt olduğuna dikkat edelim.

Sürekli Rejim : Sürekli rejimde özellikler zamanla değişmez, her birim zamanda sınırlardan geçen ısı, iş ve kütle miktarı sabittir. En sık karşımıza çıkacak sürekli rejiminde bir kontrol hacminin birinci yasa analizini yapmak istersek hem kütle korunumu hem de enerji korunumu denklemini yazmamız gerekir. Termodinamikte bu tip akışlı işlemler, Sürekli-Akışlı Sürekli-Açık işlemler ya da kısaca SASA işlemi diye anılır.

Sürekli Rejimde Kütle Korunumu Yasası : SASA işleminde, kontrol hacmi içindeki kütle zamanla sabit kalacağı için 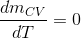$\frac{dm_{CV}}{dT}=0$ olur ve kütle korunumu denklemi aşağıdaki şekilde yazılır (S:77, Şekil 4.6):

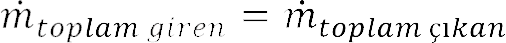
Sürekli Rejimde Enerji Korunumu Yasası : Rejim sürekli olduğunda kontrol hacmine giren ve çıkan enerjilerde her bir birim zamanda değişmeden aynı kalıyor demektir (S:78, Şekil 4.7).

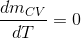$\frac{dm_{CV}}{dT}=0$ olur.

Kontrol hacmine tek akışkan girişi ve çıkışı söz konusu ise, kütle korunumu denklemini de dikkate alarak birim kütle başına SASA işleminde termodinamiğin birinci yasa ifadesini elde ederiz:

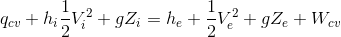
$q_{cv}+h_{i}\frac{1}{2}V_{i}^{2}+gZ_{i}=h_{e}+\frac{1}{2}V_{e}^{2}+gZ_{e}+W_{cv}$

Eğer yukarıdaki denklemde kinetik ve potansiyel enerji değişimi ihmal edilebilirse,

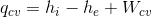$q_{cv}=h_{i}-h_{e}+W_{cv}$ bulunur.

Türbin, kompresör ve pompa gibi makinelerin (S:79, Şekil 4.9) genellikle adyabatik oldukları kabul edilir. Buna göre, aşağıda verilen denklem en sık kullanacağımız denklem olacaktır.

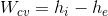
$W_{cv}=h_{i}-h_{e}$

Kısılma : Bir kanal içinden akış sırasında eğer akışkan ani bir kesit daralmasıyla karşılaşırsa basınç düşer. Kesit daralmasının hemen etrafında bir kontrol hacmi düşünürsek, iş ve ısı geçişinin olmadığı, kinetik ve potansiyel enerji değişimlerinin göz ardı edilebileceği bir durumla karşılaşırız.

Kısaca w _cv = 0 ve q _cv = 0 yazılarak h _i = h _e elde edilir.

Geçici Rejim : Uygulamada geçici rejim problemleri sistemler ilk çalıştırılmaları ya da durdurulmaları sırasında, bir kaptaki akışkanın boşaltılması ya da kabın doldurulması sırasında karşımıza çıkar. Düzgün-Akışlı Dengeli-Açık (DADA ) işlemi yaklaşımı yapılır.

Geçici Rejimde Kütle Korunumu Yasası : (DADA) işlemi kontrol hacmindeki kütle miktarı da zamanla değişecektir (S:80, Şekil 4.10). Bu durumda, kontrol hacmindeki kütlelerin ilk (1) ve son (2) anında miktarı dikkate alarak bir yaklaşım yapıyoruz. Bunun sonucunda süreklilik denklemi aşağıdaki gibi yazılır:

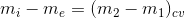
$m_{i}-m_{e}=(m_{2}-m_{1})_{cv}$

Geçici Rejimde Enerji Korunumu Yasası : DADA işlemi sırasında enerji analizini yapacağımız zaman, kontrol hacminin enerjisini bir ilk anda bir de son anda değerlendiriyoruz. Yani enerji korunumu denklemi aşağıdaki gibi yazılır:

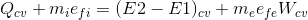
$Q_{cv}+m_{i}e_{fi}=(E2-E1)_{cv}+m_{e}e_{fe}W_{cv}$

Termodinamiğin İkinci Yasası

İkinci yasanın iki sözlü ifadesi olduğunu önceki ünitede görmüştük. Burada termodinamiğin ikinci yasasını, hem çevrimler hem de kapalı ve açık sistemlerle hal değişimi dikkate alarak ayrı ayrı inceleyeceğiz.

Tersinir İşlem ve Carnot Çevrimi : Tersinir işlem, çevrede hiçbir tesir bırakmayacak şekilde tamamen tersine işletilebilen işlemdir. Gerçek işlemlerde sürtünme, kimyasal işlemler, yanma, karışım, gazların karışımı, genişleme, ısı geçişi gibi sebeplerden hiçbir olayın tamamen tersine işletilmesi yani tersinir olabilmesi mümkün değildir.

Tersinir işlemleri referans olarak kullanabiliriz. Bu referans çevrim ise Carnot çevrimi’dir . Carnot çevriminde dört tersinir işlem vardır. Bunlar;

İki tane tersinir izotermal işlem ve
İki tane tersinir adyabatik işlemdir .

Carnot çevrimi tüm işlemleri tersinir olan böylece, iki ısı kaynağı arasında çalışan ve en büyük verime sahip tek ideal çevrimdir. Yani, sıcaklıklar Kelvin olmak üzere ikinci yasadan hareket edilerek, aşağıdaki gibi yazılır:

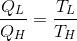
$\frac{Q_{L}}{Q_{H}}=\frac{T_{L}}{T_{H}}$

Carnot makinelerinin verimi ve performans katsayıları, çevrim için enerji korunumu dikkate alınarak, kaynak sıcaklıkları cinsinden şöyle yazılabilir:

Carnot çevriminin verimi , iş yapan akışkanın veya soğutkanın ne olduğuna bakılmaksızın, yalnızca ısı kaynaklarının sıcaklıklarına bağlıdır. Carnot makineleri, tüm işlemlerin tersinir olması nedeniyle iki ısı kaynağı arasında çalışan bütün makinelerin en verimlisi olacağına göre, aşağıdaki gibi yazılabilir:

n _{c >} n _{diğer ısı makineleri}

Aynı iki ısı kaynağı arasında çalışabilecek bütün Carnot makineleri aynı verime sahiptir. Verimi Carnot veriminden büyük makine yapılamaz.

Isı pompası (S:83, Şekil 4.13) ve soğutma makineleri (S:83, Şekil 4.14) için, performans katsayıları (literatürde kullanıldığı şekliyle Coefficient of performans – COP) aşağıdaki gibi tanımlanır:

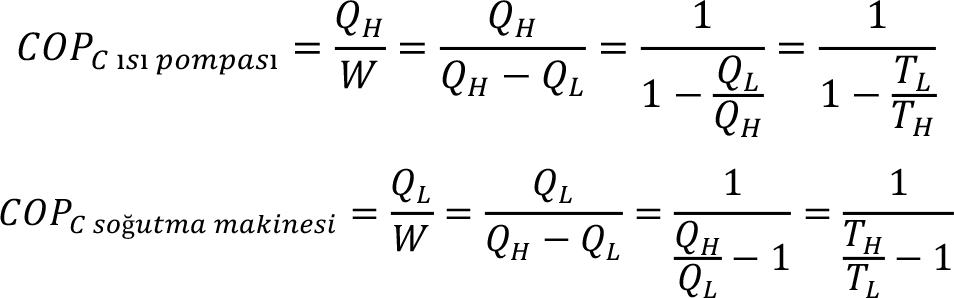
Çevrimler İçin İkinci Yasanın Analitik İfadesi

Termodinamiğin ikinci yasasının analitik ifadesi Clausius eşitsizliği olarak bilinen bir ifadeyle başlar. Clausius eşitsizliği şöyle yazılabilir:

Burada 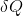$\delta Q$ makinenin çevrim boyunca geçen net ısıyı, T ise ısı geçişi sırasında sistem sınırında mutlak sıcaklığı göstermektedir.

Tersinir Hal Değişimi İçin İkinci Yasa

Tersinir hal değişimi için ikinci yasa, entropi olarak adlandırılan ve S ile gösterilen bir özellik ile verilir. Bir tersinir hal değişimi için entropi değişimi ;

Bir tersinir adyabatik hal değişimi için entropi değişimi;

S ₂ -S ₁ =0 ya da S ₂ =S ₁ olur.

Bu tersinir adyabatik hal değişimi izentropik hal değişimi olarak adlandırılır. Gerçek işlemlerde entropi değişim;

Bu da “ entropinin artışı prensibi ” olarak bilinir. Eşitsizliğin sol tarafını;

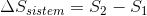$\Delta S_{sistem}=S_{2}-S_{1}$ olarak yazarsak

entropinin artma prensibini entropi üretimini temsil eden bir terim ekleyerek eşitsizlik olarak değil bir eşitlik olarak kolayca aşağıdaki gibi ifade edebiliriz:

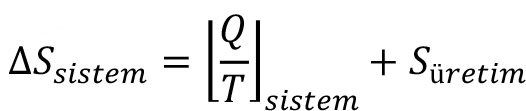
İkinci yasa analizlerinde sistem ve sistemin çevresi birlikte düşünülür ve aşağıdaki şekilde yazılır:

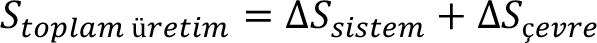
Bir Saf Maddenin Entropisi : Entropi bağımlı bir özelliktir. Kütleye bölünerek bağımsız, özgül entropi(kJ/kg.K) olarak elde edilebilir. Saf madde için doymuş sıvı ve doymuş buhar halleri ile sıkıştırılmış sıvı ve kızgın buhar halleri için değerleri termodinamik tablolardan okunabilir. Doyma bölgesinde entropinin değeri kuruluk derecesi x buhar kalitesi kullanılarak bulunur. Verilen bir x kalitesindeki buharın özgül entropisi (kJ/kg.K) aşağıdaki gibi hesaplanarak bulunur:

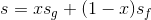
$s=xs_{g}+(1-x)s_{f}$

Burada; s doymuş ıslak buharın özgül entropisi, sf doymuş sıvının özgül entropisi ve sg doymuş buharın özgül entropisidir.

Hal değişimi yapan bir ideal gazın entropi değişimi, özgül ısılar sabit kabul edilirse, aşağıdaki şekilde hesaplanabilir:

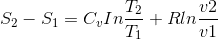
$S_{2}-S_{1}=C_{v}In\frac{T_{2}}{T_{1}}+Rln\frac{v2}{v1}$

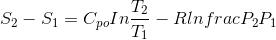
$S_{2}-S_{1}=C_{po}In\frac{T_{2}}{T_{1}}-Rlnfrac{P_{}2}{P_{}1}$

Burada R ideal gaz sabitidir.

Tersinir Sürekli Akış İşi : Sürekli akışlı bir kontrol hacminde tersinir hal değişimi için, kinetik ve potansiyel enerjilerde değişim ihmal edildiğinde, iş ifadesi için aşağıdaki şekilde yazılır:

Bu ifade sürekli rejimde çalışan türbin, kompresör ve pompa gibi açık sistemlerin analizinde geçerlidir.

Kayıp İş ve Entropi Üretimi

Bir hal değişimi sırasında tersinmezlikler varsa o zaman iş miktarının bir kısmı bu tersinmezlikler nedeniyle harcanacaktır. Öyleyse aslında sınır işini yazarken;

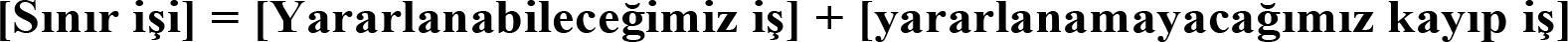
olarak düşünülmelidir. Dolayısıyla iş kayıpları entropi üretimi demektir.

Bir Kontrol Hacmi İçin İkinci Yasa

Bir kontrol hacmindeki entropi değişimi, kütleyle gelen entropiden, kütleyle çıkan entropinin çıkarılması ve ısı geçişi nedeniyle kazanılan entropi ve tersinmezlikler nedeniyle entropideki artış değerlerinin toplanması olarak ifade edilebilir. Aşağıdaki şekilde formülize edilebilir:

Sürekli Rejimde İkinci Yasa : İşlemler zamandan bağımsız olacağından entropi üretimi aşağıdaki gibi hesaplanabilir:

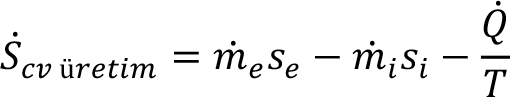
Geçici Rejimde İkinci Yasa : Geçici rejimde, geçen zamanda toplam meydana gelen değişimler düşünülerek entropi üretimi aşağıdaki gibi hesaplanabilir:

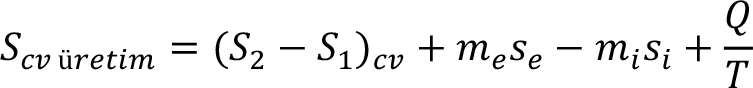
Tersinir İş ve Tersinmezlik

Bir hal değişimi sırasında bir işlem, sistemde ve çevrede hiçbir değişiklik bırakmadan yapılabiliyor ve tamamen tersine işletilebiliyorsa bu işlem tersinir işlemdir.

Çevrim İçin Tersinir İş:

Eğer herhangi bir ısı kaynağından çekilen ısı Q, bu kaynağın sıcaklığı T ve düşük sıcaklıktaki ısı kaynağına, T0 sıcaklığındaki çevre dersek, aşağıdaki gibi daha genel bir denklem yazabiliriz:

$W_{tersinir}=Q\left [ 1-\frac{T_{0}}{T} \right ]$

Sürekli Rejimde Tersinir İş : Sürekli rejim için tersinir iş, aşağıdaki şekilde hesaplanır:

$\dot{W_{cv}}=\dot{m_{i}}(e_{fi}-T_{0}s_{i})-\dot{m_{e}}(e_{fe}-T_{0}s_{e})+\dot{Q}\left [ 1-\frac{T_{0}}{T} \right ]$

Adyabatik bir kontrol hacminde birim kütle akışı için tersinir iş, aşağıdaki şekilde yazılır:

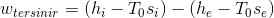
$w_{tersinir}=(h_{i}-T_{0}s_{i})-(h_{e}-T_{0}s_{e})$

Burada kinetik ve potansiyel enerji değişimleri de göz ardı edilmiştir.

Hal Değiştiren Bir Kapalı Sistemin Tersinir İşi : Sistemde kütle akışı söz konusu olmadığından, akış terimleri iptal edilerek kapalı sistemin tersinir işi bulunabilir:

$W_{tersinir}=m\left [ (e_{1}-T_{0}s_{1})-(e_{2}-T_{0}s_{2}) \right ]+Q\left [ 1-\frac{T_{0}}{T} \right ]$

Adyabatik Sistemin Birim Kütle Başına Tersinir İşi : Kinetik ve potansiyel enerji değişimleri göz ardı edilerek;

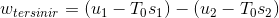
$w_{tersinir}=(u_{1}-T_{0}s_{1})-(u_{2}-T_{0}s_{2})$

ifadesiyle adyabatik sistemin birim kütle başına tersinir işi hesaplanabilir.

Tersinmezlik : Gerçek işlemlerin tersinmezliği I ile gösterilir ve aşağıdaki denklemle hesaplanır:

Ekserji

Ekserji Bir sistemin bulunduğu halden tamamen tersinir şekilde çevre ile dengeye gelinceye kadar hal değiştirmesi sağlanırsa sistem en büyük teorik yararlı işi yapmış olur ki buna kullanılabilirlik ya da ekserji adı verilir.

Basıncı ve sıcaklığı çevrenin basıncına ve sıcaklığına eşit olan sisteme ölü haldedir denir. Ölü halde bulunan sistemin ve çevrenin enerjileri vardır, fakat ekserji sıfırdır.

Ekserji bir özelliktir. Ekserji korunmaz , sistem içinde hal değişimi sırasındaki tersinmezliklerden dolayı yıkıma uğrar. Bu miktar ekserji yıkımı olarak bilinir ve entropi üretimi ile aşağıdaki ilişki geçerlidir:

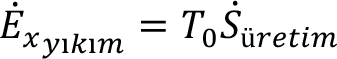
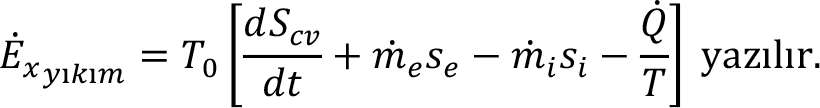
Ekserji yıkımı bir özellik değildir, çünkü tersinmezlikler işleme bağlı değişir

Isı ile Ekserji Geçişi : Isı geçişiyle sistem sınırından geçen ekserji aşağıdaki gibi hesaplanabilir.

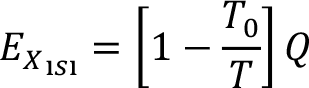
İş ile Ekserji Geçişi : İş doğrudan doğruya ekserji demektir.

E _{x iş} =W

Sınır işi olduğu durumlarda sınır işinden yararlanamayacağımız için aşağıdaki ifadeyi kullanırız:

E _{x iş} = W-P ₀ (V-V ₀ )

Kinetik Enerjinin Ekserjisi : Kinetik enerjinin ekserjisi doğrudan ekserjiye eşittir:

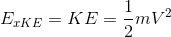
$E_{xKE}=KE=\frac{1}{2}mV^{2}$

Potansiyel Enerjinin Ekserjisi : Potansiyel enerji içinde kinetik enerjiye benzer durum söz konusudur.

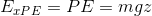
$E_{x PE}=PE=mgz$

Kapalı Sistemin Ekserji Analizi

Sistem çevre ile dengeye gelecek şekilde hal değiştirirse, yani son hal ölü hal olursa, sistemin tersinir işi en büyük olacaktır. Sistemin bulunduğu hali indissiz ifade edersek, sistemin ekserjisi :

Birim kütle başına adyabatik (q=0), hareketsiz (V=0) ve çevre ile aynı sevide (Z=0) olması durumunda sistemin ekserjisi aşağıdaki gibi yazılır:

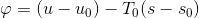
$\varphi = (u-u_{0})-T_{0}(s-s_{0})$

Kontrol Hacminin Ekserji Analizi

Kontrol hacmine kütle akışı nedeniyle aktarılan ekserji, kütlenin taşıdığı ekserji ve akış işinin ekserjisinin toplamına eşittir ve buna kısaca akış ekserjisi denilir.

Akış ekserjisi :

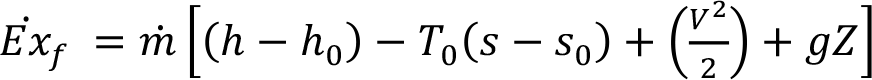
şeklindedir.

Birim kütle akışı ile aktarılan ekserji miktarı (kJ/kg):

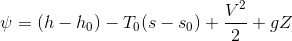
$\psi =(h-h_{0})-T_{0}(s-s_{0})+\frac{V^{2}}{2}+gZ$

İkinci Yasa Verimi ve Ekserjetik Verim

İkinci yasa verimi hesaplandığında; bir enerji kaynağının, bir santralin, bir ısı makinesinin yada soğutucunun en iyi olmaktan ne kadar uzak olduğunu anlarız .

Isı makineleri için ikinci yasa verimi :

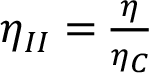
Soğutma makineleri ve ısı pompaları için ikinci yasa verimi : Kullanılan soğutma makineleri ve ısı pompaları için ikinci yasa verimi aşağıdaki şekilde hesaplanır:

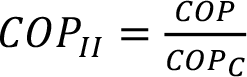
Sürekli rejimde çalışan kontrol hacimleri için ikinci yasa verimi :

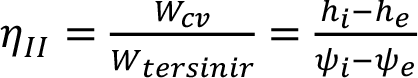
Isı geçişi olan sistemlerde ikinci yasa verimi :

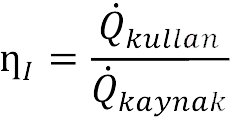
Ekserjetik verim : Aşağıdaki gibi tanımlanır: