ENERJİ YÖNETİMİ VE POLİTİKALARI - Ünite 6: Enerji Talep Tahmin Yöntemleri Özeti :

PAYLAŞ:

Ünite 6: Enerji Talep Tahmin Yöntemleri

Giriş

Dünyada hızla artan enerji talebine karşı, mevcut enerji kaynaklarının giderek azalması ve bunun yanı sıra çevre bilincinin de gelişmesi, enerjinin daha verimli bir şekilde kullanılmasını zorunlu hale getirmiştir. Toplumlar bir yandan sürekli artan nüfuslarının refahını yükseltmek için üretim yapmak, diğer yandan da temiz bir çevrede yaşamlarını sürdürmek istemektedirler. Bu bağlamda enerji-ekonomi-çevre arasındaki karşılıklı etkileşimler ve bunların sonuçları enerji politikalarının belirlenmesinde önemli olmaktadır.

Türkiye, OECD ülkeleri içerisinde son on yılda enerji talep artışı en hızlı büyüyen ülkelerden biridir. Ülkemizde gerçekleşen büyümeye paralel olarak, artan enerji talebinin doğru tahmin edilmesi bizim için son derece önem arz etmektedir. Bu bağlamda ülkemizde 20 Şubat 2001 tarih ve 4628 sayılı Elektrik Piyasası Kanununa dayanılarak Elektrik Enerjisi Talep Tahminleri Hakkında Yönetmelik hazırlanarak, 4 Nisan 2006 tarihli ve 26129 sayılı Resmi Gazetede yayınlanmıştır. Söz konusu yönetmeliğin amacı; elektrik piyasasında üretim kapasite projeksiyonu ile iletim sistemi on yıllık gelişim raporu ve dağıtım şirketlerinin yatırım planı ile dağıtım sistemi on yıllık gelişim raporunun hazırlanmasına esas teşkil eden elektrik enerjisi talep tahminlerinin oluşturulmasına ilişkin usul ve esasların belirlenmesidir. Yönetmelikte, talep tahminine esas veri seti; ekonomik, sosyal, demografik, iklimsel, çevresel veriler ve tahmin edilmeye çalışılan değişkenin geçmiş değerleri ile talep tahmin modelinin gerektirdiği diğer bölgesel verilerden oluşturulacağı belirtilmektedir.

Tahminleme

Tahminleme, gelecek olayların kestirilmesi, projeksiyonu veya öngörüsü olarak tanımlanabilir. Tahminlemenin temel fonksiyonu, elimizdeki verileri kullanarak geleceği kestirmektir.

Enerji, insan gücü, malzeme, fiyatlar vb. birçok konuda kısa, orta ve uzun vadede yapılacak doğru tahminler, alacağımız kararları etkilediği için özellikle yeni bir tesis veya kapasite artırımı gibi yüksek maliyetli projeler söz konusu olduğunda minimum hata ile yapılacak tahminleme büyük öneme sahiptir.

Herhangi bir değişkeni tahmin etmek için 6 aşama vardır:

Nelerin tahmin edileceğinin tespiti
Zaman periyodunun tespiti
Verilerin toplanması
Tahminleme yönteminin tespiti
Tahminin yapılması
Tahminin gözden geçirilmesi

Gerçeğe yakın tahminler yapmak yani hata payını düşük tutan tahmin yapmak kolay bir süreç değildir. Yapılan tahminler ile gerçekleşen değerler arasında bir fark muhakkak olacaktır. Tahmin yaparken amacımız, uygun yöntem ve tekniklerle hata payını en aza indirmek olacaktır.

Tahminleme Yöntemleri

Genel anlamda tahminleme yöntemleri; niteliksel (kalitatif) ve niceliksel (kantitatif) olmak üzere ikiye ayrılır:

Kalitatif yöntemler
- Delphi yöntemi
- Yönetici heyet görüşleri
- Pazar araştırması
Kantitatif yöntemler
- Karma yöntemler
  - Basit regresyon analizi
  - Çoklu regresyon analizi
  - Yapay zekâ ve sezgisel algoritmalar
- Zaman serisi analizi
  - Basit yaklaşımlar
  - Hareketli ortalama
  - Ağırlıklı hareketli ortalama
  - Üstel düzeltme tekniği
  - Trend analizi
  - Box-Jenkins

Kalitatif Yöntemler; görüş, deneyim, sorgulama ve uzmanlık tabanlıdır. Kantitatif Yöntemler ise bir takım istatistikisel yöntemlerle geçmiş verilerin kullanılmasına dayanır.

Kalitatif yöntemler : Niteliksel/ kalitatif tahminleme, doğası gereği sübjektif olup tahmin yapılacak alanda görev yapan uzmanların yargısına dayanır. Özellikle geçmiş verilerin olmadığı durumlarda, kurumsal planlama için orta ve uzun dönemli tahminlerin ayarlanmasında, niceliksel olarak üretilen tahminlerin ayarlanmasında ve zaman serileri gibi niceliksel teknikler tarafından üretilen paternlerin (eğilim) ayarlanmasında kullanılır. Kalitatif tahminleme, geçmişi açıklamaktan çok geleceği kestirme üzerinde durur.

Delphi yöntemi , RAND Corporation tarafından geliştirilmiştir. Bu yöntemde, ele alınan problem hakkında bilgi sahibi olduğu düşünülen uzmanlardan oluşan bir grup kullanılır. Uzmanların birbirlerinden etkilenmelerini önlemek için uzmanlara, bir dizi soru içeren anketler (satış tahminleri, vs.) ayrı ayrı gönderilir ve uzmanlar cevaplarını koordinatöre geri gönderir. Değerlendirme sonrası hangi üyenin ne tahminde bulunduğu bilgisini içermeyecek şekilde, özet bilgi uzmanlara geri gönderilir. Uzmanlar tahminlerinde ısrarcı olabilir veya değiştirebilirler. Bu şekilde bir uzlaşmaya varılıncaya kadar turlara devam edilir. Genellikle 3-4 turdan sonra uzlaşma ortaya çıkabilir.

Yönetici heyet görüşleri , kurum bünyesinde bulunan çeşitli birim yöneticilerinin bir araya gelerek, tahminleme yaptıkları yöntemdir. Yöntem, deneyimli yöneticilerin sezgileri ve yargılamaları yoluyla sundukları zengin verileri kullanma avantajına sahiptir. Sektöründe geniş bir deneyime sahip bir grup üst düzey yöneticinin uzmanlığı sayesinde tahminler üretilir.

Pazar araştırmasında , müşterilerin davranışları hakkındaki veriler, yüzyüze görüşme, telefonla görüşme, internet anketleri gibi farklı yöntemler kullanılarak toplanır. Toplanan bu veriler, istatiksel yöntemler kullanılarak, tüketici davranışları hakkında birtakım çıktılar üretilir.

Kantitatif yöntemler: Kantitatif yöntemlerden zaman serisi analizi yöntemleri tahminlemede yaygın olarak kullanılmaktadır.

Basit yaklaşımlarda , direkt olarak ortalama kullanılmaktadır. Bu yaklaşımın çok aşırı istikrarlı ortamlarda kullanılması önerilir. Bu yaklaşımda çok dikkatli olmalısınız, çünkü aşağı veya yukarı yönlü trendlerde hatalı sonuçlar alabilirsiniz. Direkt ortalama ( 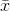$\bar{x }$ ), geçmiş tüm gözlemlerin (n) aldıkları değerlerin (?X) aritmetik ortalaması olup şu eşitlikle hesaplanır:

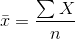
$\bar{x}=\frac{\sum X}{n}$

Hareketli ortalamalar yönteminin çok belirgin bir trend yoksa kullanılması önerilir. Kolaylıkla anlaşılan, hesaplanan ve stabil tahminler üreten bir yöntemdir. Son n adet gözlemin aritmetik ortalamasıdır. Kaç periyodun kullanılacağına deneyimle karar verilmesi gerekir ve genellikle 3 ile 8 arasında seçilir. En azından n periyotluk geçmiş verinin saklanmasına ihtiyaç duyması, trendin gerisinde kalması ve verilerdeki kompleks ilişkileri göz ardı etmesi dezavantajlarındandır. t periyot, n seçilen periyot sayısı, Y gerçek değerler ve F tahmini değerleri göstermek üzere hareketli ortalama şu şekilde hesaplanır:

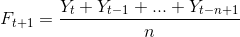
$F_{t+1}=\frac{Y_{t}+Y_{t-1}+...+Y_{t-n+1}}{n}$

Ağırlıklı hareketli ortalama , zaman serisinin geçmiş değerlerine farklı ağırlıklar (Wi) atanmasıyla hesaplanır. Böylece son verilerin etkisi artırılır. t+1. periyot için F tahmin değeri W ağırlık değerini göstermek üzere ağırlıklı hareketli ortalama ile şu şekilde hesaplanır:

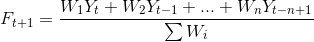
$F_{t+1}=\frac{W_{1}Y_{t}+W_{2}Y_{t-1}+...+W_{n}Y_{t-n+1}}{\sum W_{i}}$

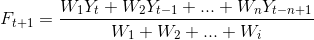
$F_{t+1}=\frac{W_{1}Y_{t}+W_{2}Y_{t-1}+...+W_{n}Y_{t-n+1}}{W_{1}+W_{2}+...+W_{i}}$

Üstel düzeltme tekniği, geçmiş verilere azalan ağırlıkların uygulandığı bir tür hareketli ortalama yöntemidir. Ağırlık 0 <? <1 aralığındadır ve genelde tahminin stabil olması için küçük bir değer seçilir (0.1 - 0.2 arası).

Yeni tahmin = (?) . (son gözlem)+ (1-?) . (son tahmin) veya

F _t+1 =?.Y _t +(1-?).F _t

?’nın seçiminde ise, N gözlem değeri olmak üzere aşağıdaki eşitlikten yararlanılır.

?=2/(N+1)

Trend analizi, regresyon modelinin dayandığı varsayımları hemen her zaman gerçekleştirememesine rağmen trendin bulunmasında yaygınlıkla kullanılmaktadır. Bu tekniğin esası, zaman ve gözlem sonuçları arasında fonksiyonel bir ilişki kurmaktır. En küçük kareler tekniğini kullanan bu yöntemde öncelikle serpilme diyagramı çizilerek bu grafiğin gelişme yönüne en uygun grafik seçilir. Doğru fonksiyonu (Y _t =a+bXt), üstel fonsiyon (Y _t =ab ^Xt ) veya parabolik fonksiyon (Y _t =a+bX _t +cX _t ² ) serpilme diyagramına göre seçilir. Doğru fonksiyonuna ilişkin normal denklemler şunlardır:

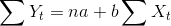
$\sum Y_{t}=na+b\sum X_{t}$

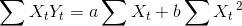
$\sum X_{t}Y_{t}=a\sum X_{t}+b\sum X_{t}\, ^{2}$

X’ler 2000, 2001,… gibi veya 1,2,3… şeklinde gösterilebilir. Ancak kolaylık açısından seri tek yıllıksa …,-2,-1,0,1,2,… şeklinde, eğer çift ise …,-3,-1,1,3,… şeklinde gösterilir ki bu durumda ?Xt=0 olur ve hesaplamada kolaylık sağlar. Bu yöntem kullanıldığında sadeleştirilmiş denklemler şu şekilde olur.

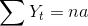
$\sum Y_{t}=na$

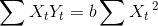
$\sum X_{t}Y_{t}=b\sum X_{t}\, ^{2}$

Box-Jenkins modelleri , en gelişmiş zaman serisi analiz yöntemidir. Belirli bir teknik değil sadece tahminlemeye bir yaklaşımdır. Uygun bir yöntem belirlemek için geçmiş verileri analiz eder ve “Autoregressive Integrated Moving Average Model” (ARIMA) veya diğer bir deyişle otoregresif-entegre-hareketli ortalama olarak adlandırılır. Bu durum dört adımdan oluşur:

Modelin belirlenmesi
Parametre tahminleri
Ayırt edici (tanı) kontrol
Ön raporlama

Otoregresif model mevcut verilerin geçmiş verilere bağlı olduğunu varsayar. Box-Jenkins cimrilik (tutumluluk) prensibine dayanır. Diğer bir ifadeyle, zaman serisi verilerinin özelliklerini ortaya koyan en uygun (en az sayıda parametre veya serbestlik derecesini göz önünde tutan) modeli kurmayı öngörür.

Karma kantitatif yöntemler arasında basit regresyon analizi, çoklu regresyon analizi, yapay zeka ve sezgisel algoritmalar yer almaktadır.

Basit regresyon analizi , biri bağımlı diğeri bağımsız olmak üzere iki değişken arasında nedensellik ilişkisi arayan bir analizdir. Bağımsız değişkenler, ortalama hava sıcaklığı gibi dış müdahale olmaksızın kendiliğinden oluşan değişkenlerdir. Bir olayın sebebi olarak görülürler.

Bağımlı değişkenler ise sonuç olarak gördüğümüz olaylardır. Ortalama hava sıcaklığı bir sebepse, doğalgaz tüketimi sonuç yani bağımlı değişkendir. Abone sayısı bağımsız bir değişken iken, elektrik tüketim miktarları bu sayıya bağımlı değişkendir. Basit regresyon analizinde amaç, trend analizinde olduğu gibi verilerimizden geçen Yt=a+bXt şeklindeki en iyi doğrunun denklemini bulmaktır. Bunun için formüller şöyledir:

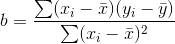
$b=\frac{\sum (x_{i}-\bar{x})(y_{i}-\bar{y})}{\sum (x_{i}-\bar{x})^{2}}$

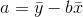
$a=\bar{y}-b\bar{x}$

Bu eşitliklerde x bağımsız değişken olarak dikkate alınırken, y ise bağımlı değişkendir. Denklemde ? ve x sırasıyla bağımlı ve bağımsız değişkenlerin aritmetik ortalamasıdır. Regresyon analizinde doğrusal ilişkinin derecesi “r” sembolü ile gösterilen korelasyon katsayısı ile ölçülür. “r” nin alacağı değerler -1 ile +1 arasında değişir ve yüksek mutlak değerler yüksek dereceli ilişkiyi gösterir. İşaretin pozitif olması bir değişken artarken diğerinin de arttığını, negatif olması ise biri azalırken diğerinin arttığını gösterir ve aşağıdaki gibi hesaplanır.

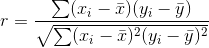
$r=\frac{\sum (x_{i}-\bar{x})(y_{i}-\bar{y})}{\sqrt{\sum (x_{i}-\bar{x})^{2}(y_{i}-\bar{y})^{2} }}$

Çoklu regresyon analizi, bir bağımlı değişkenle birden fazla bağımsız değişkenin ilişkisi arandığında kullanılır. Örneğin ürün talebi üzerinde ürünün fiyatı ve ürünü kullananların gelirleri gibi birçok değişkenin etkili olması gibi. Bu yöntemde ayrıca çoklu belirlilik katsayısı kullanılarak bağımlı değişkendeki değişmelerin yüzde kaçının bağımsız değişkenler ile açıklanabileceği sorusuna cevap bulunur. İstatiksel paket programları sayesinde yüzlerce bağımsız değişkeni modele sokmak mümkündür.

Yapay sinir ağları (YSA) tahminleme için kullanılan yöntemlerden biridir. İnsan beyin fonksiyonundan esinlenen YSA, deneme yolu ile öğrenme ve genelleştirme yapabilmektedir. YSA’nın kullanıldığı önemli alanlardan biri de geleceği tahmindir. YSA, veriler arasındaki bilinmeyen ve fark edilmesi güç ilişkileri ortaya çıkartabilir. YSA, girdi ve çıktı değişkenleri arasındaki herhangi bir ön bilgiye ihtiyaç duymadan, herhangi bir varsayımda bulunmadan, doğrusal olmayan modellemeyi sağlayabilmektedir. Ağa, girdi bilgileri ve bu girdilere karşılık gelen çıktı bilgileri verilmekte ve ağın girdi-çıktı arasındaki ilişkiyi öğrenmesi sağlanmakta, böylece ağın eğitimi gerçekleştirilmektedir. Öğreticili öğrenme olarak adlandırılan bu yöntem genelde tercih edilen bir yöntemdir.

Bir diğer yöntem ise genetik algoritmalardır . Evrim teorisine dayanan, popülasyon tabanlı bir yöntemdir. Çözüm genlerden oluşan kromozomlarla ifade edilir. Kromozomların veya bireylerin bir uyum değeri vardır.

Daha iyi değerlere sahip olanların yaşama şansı yüksektir. Durma kriteri sağlanana kadar popülasyondaki bireyler seçme, çaprazlama ve mutasyon işlemlerine tabi tutulurlar. Bunların dışında karınca kolonileri, tavlama benzetimi gibi meta-sezgisellerde tahminleme için kullanılabilir.

Tahminleme Doğruluğunun Ölçülmesi

Tahminleme için kullanılan yöntemlerin doğruluğunu ölçmek için kullanılan performans kriterleridir. Gerçek değerlere yakınlık yöntemin başarılı olduğunu gösterir. Birden fazla yöntemin uygulandığı veya aynı yöntemi farklı parametrelerle çalıştırdığımız durumlarda karşılaştırma için kullanılabilir. Bu kriterler şu şekilde hesaplanır:

Tahmin Hatası = Gerçek değer – Tahmini değer
Bias (Ortalama Hata) = ? (Hata) / n
Ortalama Hata Kareleri (OHK) = ? (Hata) ² / n
Ortalama Mutlak Hata (OMH) = ? I Hata I / n
Ortalama Mutlak Hata Yüzdesi (OMHY) = ?I(Hata/Gerçek değer) * 100 I / n