FİNANSAL YÖNETİM I - Ünite 3: Paranın Zaman Değeri Özeti :

PAYLAŞ:

Ünite 3: Paranın Zaman Değeri

Para Neden Zaman Değerine Sahiptir?

İşletmeler gibi kişiler de; “nereden kredi bulabilirim, hangi kredinin maliyeti daha uygundur” gibi finansman kararlarıyla ve “nereye, ne tür yatırım yapabilirim” gibi yatırım kararlarıyla karşı karşıyadır.

Paranın zaman değeri para akışının farklı zamanlarda gerçekleşmesinden kaynaklanmaktadır. Alınan veya verilen paranın o günkü kullanım hakkından vazgeçilmesinin bir bedeli vardır.

Faiz; parayı sunanlar için bugünkü kullanım hakkından vazgeçmenin getirisi olurken, parayı talep edenler için de gelecekte kullanılacak parayı bugün kullanmanın bedelidir. Faizi; enflasyon, likidite, ödenmeme riski, vadenin uzunluğu gibi faktörler etkilemektedir. Enflasyonla faiz karıştırılmamalıdır. Enflasyonist ortamlarda faiz oranlarının artıyor olması doğaldır. Yatırım ve kredi işlemlerinde enflasyon dışında likidite, ödenmeme, vade gibi faktörler de faiz oranlarını etkilemektedir. Uzun vadeli borç vermede ya da uzun vadeli yatırımlarda beklenen faizin ya da getiri oranının daha yüksek olmasının temel nedeni, vadeyle artan risktir.

Basit Faiz Hesaplamaları

Paranın zaman değerinin hesaplanmasında basit ya da bileşik faiz yöntemi kullanılabilir.

Basit Faiz: Faizin, aynı anapara üzerinden hesaplandığı faiz hesaplama şeklidir.

Bileşik Faiz: Faizin her devre değişen parçalar üzerinden hesaplandığı faiz hesaplama şeklidir. Genellikle bir yıldan daha kısa vadeli finansal işlemlerde basit faiz, bir yıldan uzun vadeli işlemlerde bileşik faiz kullanılmaktadır. Günümüzde ülkelerin ve piyasaların özelliklerinden dolayı kısa vadeli işlemlerde de bileşik faiz kullanılmaktadır.

I: Basit faiz tutarını

P: Anaparayı

i: Faiz oranını

t: Zaman, süreyi göstermek üzere

Faiz; I=P * i * t

Formülü ile hesaplanır. Burada faiz oranı ile sürenin uyumlu olmasına dikkat edilmelidir. Eğer faiz oranı yıllık olarak verilmişse süre de yıllık; faiz oranı aylık ya da günlük olarak verilmişse, süre de aylık ya da günlük olarak ele alınmalıdır.

Örneğin; Bir kredi kurumuna 10.000 TL % 12 faiz oranıyla yatırılmıştır:

a) Bu paranın 1.yıl sonundaki faizi;

P = 10.000 TL, i = 0,12 (yıllık), t = 1 (yıl), I = ?

I = 10.000 * 0,12 * 1

I = 1.200 TL

b) Bu paranın 3.ay sonundaki faizi;

t = 3 ay = 3/12 yıl, I = ?

I = 10.000 * 0,12 * 3/12

I = 300 TL

c) Bu paranın 95 gün sonraki faizi;

t = 95 gün = 95/360 yıl, I = ?

I = 10.000 * 0,12 * 95/360

I = 317 TL

Basit Faizde Gelecek Değer

Bir paranın, belirli bir süre sonunda, belirli bir faiz oranıyla ulaşacağı değere paranın gelecekteki değeri denir.

S: Gelecekteki değer

S=P+I

S=P(1+i*t) formülü kullanılır.

Örneğin; Bir işletme bir bankadan 8 hafta için, %13 faizle 40.000TL kredi almıştır.

a) İşletme kaç TL geri ödemede bulunacaktır?

P = 40.000 TL, i = %13, t = 8 hafta = 8/52 yıl, S = ?

S = P (1 + i * t)

S = 40.000 (1 + 0,13 * 8/52)

S = 40.800 TL

b) İşletme ne kadar faiz ödeyecektir?

I = S-P=40.800-40.000 = 800 TL

Basit Faizde Bugünkü Değer

İskontolama, gelecekteki bir değerin, belirli bir iskonto oranıyla indirgenerek bugünkü değerini hesaplama işlemidir. Finansal kararlarda iskontolama işlemleriyle sık sık karşılaşılır. Gelecek bir tarihteki paranın şimdiki değerini bulmada ya da senetlerin vade tarihinden önce paraya dönüştürülmesinde iskontolama işlemleri yapılacaktır.

Bugünkü değer, gelecek değerle ilgili eşitlikten

faydalanılarak aşağıdaki formülle hesaplanabilir;

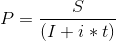
$P=\frac{S}{(I+i*t)}$

Örneğin; Bir işletmenin 6 ay sonra alacağı 100.000TL yerine, piyasa faiz oranları %16 olduğunda, bugün hangi değerde bir parayı kabul etmelidir?

S = 100.000 TL

i = %16

t = 6 ay = 6/12 yıl

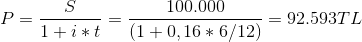$P=\frac{S}{1+i*t}=\frac{100.000}{(1+0,16*6/12)}=92.593TL$ alması gerekecektir.

Hazine bonolarının ikincil piyasaları da vardır. Yani hazine bonosu alanlar, vade tarihine kadar her an “hazine bonosu” tekrar satabilirler. Bononun satış zamanında hangi değerle satılacağı yine aynı hesaplama mantığı ile bulunacaktır. Hazine bonolarının bugünkü değeri iç ya da dış iskonto yöntemine göre hesaplanabilir. Dış iskonto yöntemi kullanıldığında, iskonto tutarı bononun vade değeri üzerinden hesaplanır. İskonto tutarı vade değerinden düşüldüğünde bugünkü değer hesaplanmış olur.

Bileşik Faiz Hesaplamaları

Genellikle kısa vadeli finansal işlemlerde basit faiz, uzun vadelilerde bileşik faiz kullanılır. Basit faizle bileşik faiz arasındaki en önemli fark basit faizde sermaye her devre için değişmezken, bileşik faizde her devre için bir önceki devrenin faizi kadar artmasıdır.

Sn: Gelecekteki değeri,

P: Anaparayı,

n: vade boyunca devre sayısını göstermek üzere,

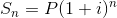
$S_{n}=P(1+i)^{n}$

formülünden bulunmaktadır.

Örneğin; Bir girişimci 5 yıl sonra yapacağı bir yatırım

için bugün bir bankada 50.000 TL’lik hesap açtırmıştır.

Bankanın uygulayacağı faiz oranı %12 ise girişimcinin

5.yıl sonunda bankada biriken parası ne olacaktır?

P = 50.000 TL, i = 0,12, n = 5 yıl, S = ?

S = P(1 + i)n

S = 50.000 (1,12)5 = 88.117 TL olur. Bu rakam 50.000

TL’nin yıllık %12 faizle, 5 yıl sonundaki değeridir.

Bileşik Faizde Bugünkü Değer

Bileşik faize göre bugünkü değer aşağıdaki eşitlikle bulunur.

Sn: Gelecekteki değeri,

P: Anaparayı,

n: vade boyunca devre sayısını göstermek üzere

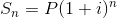
$S_{n}=P(1+i)^{n}$

formülünden bulunmaktadır.

Örneğin; Bir girişimci 5 yıl sonra yapacağı bir yatırım için bugün bir bankada 50.000 TL’lik hesap açtırmıştır. Bankanın uygulayacağı faiz oranı %12 ise girişimcinin 5.yıl sonunda bankada biriken parası ne olacaktır?

P = 50.000 TL, i = 0,12, n = 5 yıl, S = ?

S = P(1 + i)n

S = 50.000 (1,12)5 = 88.117 TL olur. Bu rakam 50.000 TL’nin yıllık %12 faizle, 5 yıl sonundaki değeridir.

Bileşik Faizde Bugünkü Değer

Bileşik faize göre bugünkü değer aşağıdaki eşitlikle bulunur:

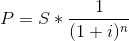
$P=S*\frac{1}{(1+i)^{n}}$

Yukarıdaki eşitlikteki $\left [ \frac{1}{(1+i)^{n}} \right ]$ indirgeme faktörü olarak adlandırılır.

Örneğin; 5. yıl sonunda alacağınız 25.500 TL yerine faiz oranı %5 iken peşin olarak hangi parayı kabul edersiniz?

i = 0,05, n = 5, S = 25.500 TL, P = ?

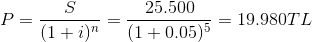
$P=\frac{S}{(1+i)^{n}}=\frac{25.500}{(1+0.05)^{5}}=19.980TL$

Nominal Faiz, Efektif Faiz ve Enflasyon

Nominal faiz: işleme konu olan veya finansal varlıkların üzerinde yazılı olan faiz oranıdır.

Efektif faiz: faizin bileşik faizle ve yıldan daha kısa süre için hesaplanması durumunda gerçekleşen faizdir.

j: Yıllık nominal faiz oranını
m: Devre sayısını
i: Devre faiz oranını
r: efektif faizi
göstermektedir.

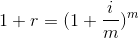$1+r=(1+\frac{i}{m})^{m}$ kısaca

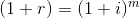$(1+r)=(1+i)^{m}$ formülünden hesaplanmaktadır.

Faiz Oranlarının Enflasyondan Arındırılması

Enflasyon zaman içinde mal ve hizmet fiyatlarının ortalama düzeyinin yükselmesidir. Farklı zaman noktalarındaki mal ve hizmet fiyatlarının karşılaştırılması, paranın satın alma gücündeki değişmeler nedeniyle anlamlı değildir. Bu durumda mal ve hizmetlerin nominal değeri yerine reel değerinin karşılaştırılması gerekmektedir. Enflasyonist ortamlarda fon arz edenlerin nominal faizden daha çok reel getiriyi bilmeleri gerekmektedir.

Enflasyon: zaman içinde mal ve hizmet fiyatlarının ortalama düzeyinin yükselmesidir. Örneğin nominal faiz %10, piyasa enflasyon oranı %10 olarak gerçekleşirse yatırımcının reel getirisi sıfır olmuştur. Yani nominal faiz, reel faiz ve enflasyon arasında

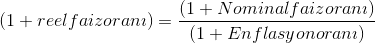
$(1+reel faiz oran\imath )=\frac{(1+Nominal faiz oran\imath )}{(1+Enflasyon oran\imath )}$

şeklinde bir ilişki bulunmaktadır.

Örneğin; bir devlet tahvilinin nominal faizi %14, o yıl ekonomide beklenen enflasyon oranı da %10 olduğuna göre yatırımcının reel getiri oranı;

$1+Reel Faiz Oran\imath =\frac{(1+0,14)}{(1+0,10)}$

Reel Faiz Oranı=%3,64

Örneğin; Enflasyon her devre (soruda aylık enflasyon oranı verilmiştir) %2 oranında arttığına göre enflasyonun 12 devre sonundaki değeri sorulmaktadır. Dolayısıyla bileşik faizde “efektif faiz” hesaplarken kullanılan formülden faydalanarak yıllık enflasyon oranı bulunabilir. Çünkü enflasyon da bileşik faiz gibi büyüme özelliğine sahiptir.

(1 + Aylık Enflasyon Oranı) ¹² = (1 + Yıllık Enflasyon Oranı)

Yıllık Enflasyon Oranı = (1 + 0,02) ¹² -1

Yıllık Enflasyon Oranı = %26,82

Eşit Taksitli Ödemeler (Anüiteler)

Taksitlerin eşit, devre faiz oranının ve devre süresinin değişmediği ödemeler serisine Anüite denir.

Örneğin kira ödemeleri, tahvil faizleri, eşit taksitlerle ödenecek krediler gibi ödemelerde anüite kullanılır.

Eşit Ödemeler Dizisinin Gelecekteki Değeri

Anüitenin gelecek değeri aşağıdaki formülle hesaplanabilir;

A: Her devre alınacak ya da verilecek eşit taksitler

n: Devre sonu

i: Faiz oranı

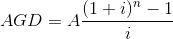
$AGD=A\frac{(1+i)^{n}-1}{i}$

Örneğin; Bir işletmenin 10 yıl sonra ödenmesi gereken borcu için her yılsonunda bankaya 7.000 yatırması gerekmektedir. Bu işletmenin 10. yıl sonunda biriken parası ne kadardır? (Faiz oranı %8’dir.)

n = 10, A =7.000 TL, i = 0,08, AGD = ?

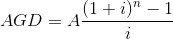
$AGD=A\frac{(1+i)^{n}-1}{i}$

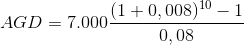
$AGD=7.000\frac{(1+0,008)^{10}-1}{0,08}$

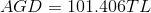
AGD=101.406 TL

Eşit Ödemeler Dizisinin Bugünkü Değeri

Her devre alınacak ya da verilecek eşit taksitlerin bugünkü değeri aşağıdaki formülle hesaplanabilir;

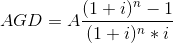
$AGD=A\frac{(1+i)^{n}-1}{(1+i)^{n}*i}$

Sürekli Anüiteler

Taksit sayısının belirli olmadığı, taksitlerin sürekli olarak devam edeceğinin varsayıldığı anüitelerdir. Devamlı olarak yapılacak eşit ödemelerin bugünkü değeri aşağıdaki formülle hesaplanabilir;

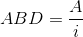
$ABD=\frac{A}{i}$

Örneğin devamlı olarak yılda 45 TL kâr payı ödemesi taahhüt edilen bir imtiyazlı hisse senedinin değeri, yatırımcının istediği getiri oranı %20ise,

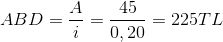
$ABD=\frac{A}{i}=\frac{45}{0,20}=225 TL$

Borç Geri Ödemeleri

Anüitelerin en önemli uygulama alanlarından biri uzun vadeli borçların amortismanıdır. Alınan kredi karşılığında ödenecek eşit taksitlerin bugünkü değeri, alınan krediye eşit olacaktır. Bu durumda anüitenin bugünkü değerini veren formülden faydalanmak gerekir.

Örneğin bir işletme bugün almış olduğu 500.000 TL’lik bir krediyi, yıllık eşit taksitlerle 5 yılda geri ödeyecek olsun. Yıllık faiz oranı %18 olduğuna göre, eşit taksitler nasıl hesaplanabilir?

Alınan kredi karşılığında ödenecek eşit taksitlerin bugünkü değeri, alınan krediye eşit olacaktır. Diğer bir ifade ile burada anüitenin bugünkü değerini veren formülden yararlanılır.

ABD = 500.000 TL, n = 5, i = 0,18, A= ?

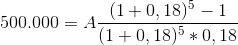
$500.000=A\frac{(1+0,18)^{5}-1}{(1+0,18)^{5}*0,18}$

A= 159.889 TL olarak bulunur.

İşletme almış olduğu 500.000 TL’lık krediyi, 5 yılda 159.889 TL’lık taksitlerle geri ödeyecektir.

Geciktirilmiş Eşit Taksitli Ödemeler (Geciktirilmiş Anüiteler)

Geciktirilmiş ödemelerde, ilk ödeme, ilk devrenin bitiminden sonra herhangi bir zamanda yapılır. Normal anüitede kullanılan formülden hareketle geciktirilmiş ödemelerin bugünkü değer (ABDg) eşitliği aşağıdaki şekilde yazılabilir;

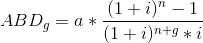
$ABD_{g}=a*\frac{(1+i)^{n}-1}{(1+i)^{n+g}*i}$

Örneğin; 3 sene ödemesiz olmak üzere alınan bir borç, her yıl 500.000 TL’lik eşit taksitlerle 5 senede geri ödenecektir. Faiz oranı %12 ise alınan borç miktarı nedir?

n = 5, a = 500.000 TL, g = 3 (geciktirilme süresi), i = %12

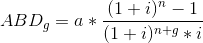
$ABD_{g}=a*\frac{(1+i)^{n}-1}{(1+i)^{n+g}*i}$

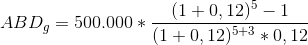
$ABD_{g}=500.000*\frac{(1+0,12)^{5}-1}{(1+0,12)^{5+3}*0,12}$

ABD! = 1.282.904 TL olarak bulunur.

Kalan Borç Miktarının, Eşit Taksitlerdeki Faiz ve Anapara Payının Hesaplanması

Hem borç alanlar hem de borç verenler sık sık herhangi bir tarihteki kalan borç miktarını bilmek ister. Faiz ödemeleri vergiden düşülebilen bir giderdir. Bu nedenle işletmeler ödedikleri borç taksitlerinde ne kadar faiz ödendiğini hesaplamak durumundadırlar. Tüm taksitlerin eşit olması durumunda ödemeler, normal anüite formülünden faydalanılarak bulunur. Belirli bir tarihteki kalan borç ise; ödenmemiş taksitlerin bugünkü değeriyle hesaplanır.

Konu ile ilgili çözülmüş örnekler için kitabınızın 77-78. Sayfaları incelenebilir.