İŞLETME ANALİTİĞİ - Ünite 7: İşlemtablolarıyla Kestirimci Analitik Özeti :
PAYLAŞ:Ünite 7: İşlemtablolarıyla Kestirimci Analitik
Giriş
Örneklemenin temel amacı, ana kütle için tanımlı bir veya daha fazla rassal değişkenin özelliklerine ilişkin doğru bilgi elde edebilmektir. Örneklemede yapılan temel işlem ana kütle parametrelerinin, örneklemden hesaplanan istatistikler yardımıyla tahmin edilmesidir.
İstatistiksel çıkarım problemleri, tahminleme ve hipotez testleri olarak incelense de, temel olarak bunların bütünü karar alma problemini oluşturur. Bu iki süreç arasındaki fark:
- Tahminleme probleminde ana kütle parametresinin ya da parametrelerinin sahip olduğu değer/değerlerinin belirlenmesi gereklidir.
- Hipotez testlerinde parametrelerin aldığı belirli değerlerin kabulü ya da reddedilmesi kararının verilmesi gerekliliğidir.
Tahminleme : Örneklem seçimi sonucunda hesaplanan istatistik aracılığı ile ana kütle parametresinin aldığı değer olarak kabul edilen bir aralık ya da bir sayı elde etme işlemidir.
Örneklem bilgisi , bir başka deyişle örneklem istatistikleri yardımıyla ana kütle parametrelerinin tahmin edilmesi iki yöntemle gerçekleştirilir:
- Nokta tahminlemesi
- Aralık tahminlemesi
Nokta tahmini , bir ana kütle parametresinin tahmininde kullanılan istatistik değeridir.
Aralık tahmini , tahminin parametreye yakınlık derecesinin belirlenmesi için nokta tahmini yerine kullanılan yöntemdir.
Ana kütle parametresinin içerisinde yer alacağı tahmin edilen ve belli bir güven düzeyine göre belirlenen sayısal değerler aralığına güven aralığı denir.
İşlemtablolarıyla Güven Aralığı
Normal dağılıma sahip ana kütleler için ana kütle aritmetik ortalamasının (µ) iyi bir nokta tahmincisi örneklem aritmetik ortalamasıdır
 . Ancak örneklemden hesaplanan aritmetik ortalama değerinin gerçek ana kütle ortalamasından bir miktar az ya da bir miktar fazla olması kaçınılmazdır. Bu nedenle yapılan tahminin doğruluğundan emin olmak istendiğinde ana kütle aritmetik ortalamasının, gözlenen örneklem aritmetik ortalama değerine tam olarak eşit olduğu söylenemez. Bunun yerine
. Ancak örneklemden hesaplanan aritmetik ortalama değerinin gerçek ana kütle ortalamasından bir miktar az ya da bir miktar fazla olması kaçınılmazdır. Bu nedenle yapılan tahminin doğruluğundan emin olmak istendiğinde ana kütle aritmetik ortalamasının, gözlenen örneklem aritmetik ortalama değerine tam olarak eşit olduğu söylenemez. Bunun yerine
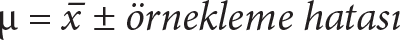
şeklinde bir aralık tahmini ya da güven aralığı oluşturmak gerekir. Örnekleme hatasının büyüklüğü, örneklem aritmetik ortalamasının ne kadar değişim gösterdiğine bağlı olarak değişir.
Merkezî limit teorimine göre; ortalaması µ ve standart sapması ? olan herhangi bir ana kütleden iadeli seçimle çekilen örneklem ortalamalarının dağılımı, n örneklem hacmi büyüdükçe ortalaması µ ve standart sapması
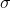 /
/
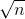 olan Normal dağılıma yaklaşır. Bu teoremde, dikkat edilmesi gereken iki nokta şunlardır:
olan Normal dağılıma yaklaşır. Bu teoremde, dikkat edilmesi gereken iki nokta şunlardır:
- İncelenen değişken Normal dağılıma sahip olduğunda, herhangi bir n örneklem hacmi için, örneklem ortalamalarının dağılımı da Normal dağılımdır.
- İncelenen değişkenin dağılımı belli değil ise, örneklem ortalamalarının dağılımının Normal dağılıma yaklaşabilmesi için örneklem hacmi n ? 30 olmalıdır. Örneklem ne kadar büyükse, yaklaşım o kadar iyi olur.
İşlemtablolarında Normal dağılım kullanılarak bir ana kütle ortalamasının güven aralığı GÜVENİRLİK işlevi yardımıyla hesaplanır.
Yazımı: GÜVENİRLİK(alfa;standart_sapma;boyut)
İşlev yazımındaki parametreler:
- Alfa: Güvenirlik düzeyini hesaplamak için kullanılır, gereklidir. Güvenirlik düzeyi (1- Alfa)’ya eşittir. Alfa için genellikle 0,01 ve 0,05 değerleri kullanılır. Alfa’nın 0,05 olması durumunda güvenirlik düzeyi 0,95 ve alfa’nın 0,01 olması durumunda güvenirlik düzeyi 0,99 olacaktır.
- Standartsapma: Örneklem standart sapmasıdır, gereklidir.
- Boyut: Ana kütle içinden çekilen örneklem sayısıdır, gereklidir.
İşlemtablolarıyla Hipotez Testleri Ve Varyans Analizi
Hipotez , bir araştırmaya başlanmadan önce ortaya atılan ve doğru olup olmadığı araştırılacak olan yargıdır. Hipotez testi, özellikleri bilinen bir ana kütleden elde edilen örneklem istatistiğinin ana kütle parametresiyle karşılaştırılıp test edilmesidir. Örneklem parametresi anakütle parametresine yakın ise ortaya atılan hipotez doğru olarak kabul edilir. Aksi halde hipotez red edilir. Hipotez testini gerçekleştirmek için öncelikle sıfır hipotezi ve alternatif hipotezin basit ve açık bir şekilde ifade edilmiş olması gerekir.
Sıfır hipotezi , H0 simgesi ile gösterilir ve yokluk hipotezi veya istatistiksel hipotez de denir. Sıfır hipotezinin aksi ispatlanana kadar doğru olduğu kabul edilir. Hâlihazırda olan durumun devam ettiğini, ana kütle parametresinin değerinde bir değişiklik olmadığını gösterir.
Alternatif hipotez ; karşıt hipotez veya araştırma hipotezi olarak da bilinir ve H1 simgesi ile gösterilir. Sıfır hipotezinin red edilmesi durumunda kabul edilecek ifade veya değeri gösterir. Sistemde bir değişiklik yapıldıysa, bu değişikliğin uygunluğunun test edilebilmesini sağlayacak biçimde ifade edilir.
İstatistikte gerçekte doğru olan H 0 hipotezinin yanlış diye red edilmesine I. tip hata denir. I. tip hata yapma olasılığı ? ile gösterilir. II. tip hata ise, gerçekte doğru olmayan H 0 hipotezinin doğru olarak kabul edilmesi durumudur ve II. tip hata yapma olasılığı ß ile gösterilir. I. tip hata yapma olasılığı ? ise, doğru olan H 0 hipotezinin doğru olarak kabul edilmesi olasılığı bunun tamamlayanıdır (?= %5 ise H0 hipotezinin doğru olarak kabul edilmesi olasılığı %95). Bu olasılığa testin güvenilirlik düzeyi denir. Gerçekte yanlış olan H 0 hipotezinin red edilmesi olasılığı 1-ß ile ifade edilir ve buna da testin gücü denir.
Örneklem büyüklüğüne bağlı olarak, yapılacak hipotez testlerinin farklılık göstermektedir. Ana kütleden seçilen örneklem büyüklüğü n, 30 birime eşit veya daha fazla ise z testi, 30 birimden daha küçükse Student-t testi uygulanır.
İstatistiksel kararın verilmesi, H 0 hipotezinin kabul veya red edilmesidir. Bu kararın verilebilmesi için kritik değer denilen ölçütün belirlenmesi gereklidir. Test istatistiğinin kritik değeri, bir örnekleme dağılımında H 0 hipotezinin red bölgesinin başlama noktasını gösteren değerdir. Kritik değer, seçilen alfa anlamlılık düzeyine, H 1 hipotezinin ifade ediliş biçimine ve örneklem istatistiğinin dağılım şekline bağlıdır. Alternatif hipotez (H 1 ):
- Eşitsizlik şeklinde ifade edilirse, hipotez testi çift yönlü ,
- Büyüklük veya küçüklük şeklinde ifade edilirse, hipotez testi tek yönlü ,
Tek örneklem z testi , bir ana kütleden rassal olarak elde edilen örneklemin aritmetik ortalamasıyla, bu örneklemin elde edilmesinde kullanılan ana kütle aritmetik ortalamasına ilişkin önceden bilinen bir değer arasında farklılığın istatistiksel olarak anlamlı olup olmadığının araştırılması için kullanılır.
İşlemtablolarında tek örneklem z testi Z.TEST işleviyle gerçekleştirilir.
Yazımı: Z.TEST(dizi;x;sigma)
İşlev yazımındaki parametreler:
- Dizi: Gözlem değerlerinin bulunduğu aralık, gereklidir.
- x:Sınanacak değer, gereklidir.
- Sigma: Ana kütle standart sapması biliniyorsa yazılır, belirtilmezse örneklem standart sapmasıdır, isteğe bağlıdır.
Z.TEST işlevi kullanılırken, dikkat edilmesi gereken en önemli nokta alternatif hipotezin oluşturulma biçimidir. Eğer alternatif hipotez, yön bildirecek biçimde “büyüktür” veya “küçüktür” ifadesini içeriyorsa, işlev sonucu hesaplanan olasılık değeri doğrudan araştırmacının ? değeri ile karşılaştırılarak karar verilebilir. Bu durum tek yönlü hipotez testi olarak da adlandırılır. İşlev sonucunda elde edilen olasılık değeri ? değerine eşit veya büyük ise sıfır hipotezi kabul edilir. Aksi durumda, işlev sonucunda elde edilen olasılık değeri ? değerinden küçük ise sıfır hipotezi red edilerek, alternatif hipotezin doğru olduğu ifade edilir. Eğer alternatif hipotez, çift yönlü olarak veya eşitsizlik biçiminde kuruldu ise, ? ile karşılaştırılacak olasılık değerinin hesaplanması için Z.TEST işlevinin izleyen özel biçimi kullanılır:
2xMİN(Z.TEST(dizi;x;sigma);1-Z.TEST(dizi;x;sigma))
Bu işlevin çalıştırılması ile elde edilen olasılık değeri ? ile karşılaştırılarak karar verilir. Karşılaştırma işlemi tek yönlü hipotez testindeki ile aynıdır.
İki ana kütleye ilişkin z testi : Üzerinde durulan araştırma konusuna ilişkin iki ayrı ana kütle ele alınarak, bu ana kütlelerin aritmetik ortalamaları arasında bir fark olup olmadığının araştırıldığı testtir. Burada önemli olan iki ana kütlenin parametreleriyle ilgili hipotez testlerinin dayandığı varsayımlardır. Bu varsayımlar şu şekilde sıralanır;
- Ana kütlelerden elde edilen örneklemlerin Normal dağılıma sahip olması,
- Örnekleme seçilen birimlerin iadeli seçimle ve eşit olasılıkla belirlenmesi veya ana kütlelerin sonsuz büyük olması,
- İki ana kütleden elde edilen örneklemlerin seçiminin birbirinden bağımsız olması,
Tek örneklem Student-t testi: Elde edilen örneklemin Normal dağılıma sahip bir ana kütleden geldiği varsayımı altında ve örneklem büyüklüğünün 30’dan küçük olması durumunda yapılan hipotez testidir. Bu test ile örneklemin, ortalaması bilinen ve Normal dağılan bir ana kütleden gelip gelmediği araştırılır. İşlemtablolarında tek örneklem Student-t testi T.DAĞ.2K işleviyle gerçekleştirilir.
Yazımı: T.DAĞ.2K(x;serbestlik_derecesi)
İşlev yazımındaki parametreler:
- x: Sınanacak değer, gereklidir.
- Serbestlik_derecesi: Gözlem sayısından 1 çıkartılarak elde edilen değerdir, gereklidir.
Bağımsız iki örneklem Student-t testi: Örneklem büyüklüğü 30’dan küçük olması durumunda, Normal dağıldığı varsayılan farklı iki ana kütleden gelen örneklemlerin ortalamalarının karşılaştırılmasında kullanılan testtir.
Bağımlı iki örneklem Student-t testi: Bu testte de bağımsız iki örneklem Student-t testinde olduğu gibi iki örneklem ortalaması karşılaştırması yapılır. Ancak burada Normal dağıldığı varsayılan ana kütleden elde bir örneklem üzerinde öntest ve sontest değerleri arasında bir fark olup olmadığı araştırılır.
İşlemtablolarında bağımlı iki örneklem Student-t testi T.TEST işleviyle gerçekleştirilir.
Yazımı: T.TEST( dizi1;dizi2;yazı_say;tür )
İşlev yazımındaki parametreler:
- Dizi1: Birinci veri kümesi, gereklidir.
- Dizi2: İkinci veri kümesi, gereklidir.
- Yazı_say: Tek taraflı test için 1, çift taraflı test için 2 değeri yazılır, gereklidir.
- Tür: Uygulanacak Student-t testini belirtir, bağımlı ise 1, iki örneklem eşit varyans için 2, iki örneklem eşit olmayan varyans için 3 değeri yazılır, gereklidir.
Varyans analizi ile dağılımların toplam değişkenliğini çeşitli bileşenlere ayırma yöntemi yardımıyla bağımsız değişkenlerin bağımlı değişkenler üzerindeki etkileri incelenebilmektedir.
Tek yönlü varyans analizinde gözlem değerleri tek bir bağımlı değişkene göre gruplandırılır ve bu gruplara ilişkin ana kütle aritmetik ortalamaları karşılaştırılır. İkiden fazla ana kütle ortalamasının karşılaştırılmasında Z ya da t-testleri kullanılamamakla birlikte bu karşılaştırma için F-testinden yararlanılır. F-testinde kullanılan F-istatistiği , aynı varyansın iki ayrı birbirinden bağımsız tahmininin birbirine oranıdır. Bu oran, yani F-istatistiğinin örnekleme dağılımı da F-dağılımı olarak bilinir.
Varyans analizinde genellikle değişkenliğin bileşenlere ayrılmasıyla birlikte değişim kaynağının bulunmasıyla da ilgilenilir. Değişkenliğin ayrıştırılması işlemi, kareler toplamları ve kareler oranlarının hesaplanması yoluyla gerçekleştirilir. Dolayısıyla F-testi uygulanması sonucu, değişim yani model denklemi kaynaklara ayrılmış olur. Değişkenlik hatadan ya da gruplardan kaynaklanabilir.
Toplam Değişkenlik = Grup Etkisi + Hata
Varyans analizi uygulanabilmesi için sağlanması gereken koşullar:
- Grupların belirlendiği ana kütleler Normal dağılıma sahip olmalıdır.
- Karşılaştırılan gruplar birbirinden bağımsız olmalıdır.
- Grupların varyansları eşit olmalıdır.
Varyans analizinde toplam değişim bileşenlerine ayrıldığı için üçüncü koşul çok önemlidir. Çünkü farklı varyanslı grup ortalamaları karşılaştırıldığında gruplar arası değişim için sistematik hata yapılmış olur.
İşlemtablolarıyla Korelasyon Ve Basit Doğrusal Regresyon Analizi
Korelasyon analizi’nin en genel tanımı değişkenler arasındaki ilişkilerin incelenmesidir. Değişkenler arasında var olabilecek ilişkinin derecesinin tespit edilebilmesi amacı ile çeşitli teknikler kullanılabilir. En basit şekli ile iki değişken arasındaki ilişkiyi gözlemlemek için bu değişkenlerin saçılım grafikleri çizilebilir. Grafiklerin yanında ilişkinin derecesini gösteren istatistiklere de ihtiyaç duyulur.
İstatistiklerden biri Pearson korelasyon katsayısı ’dır. İki ya da daha fazla ve en az aralıklı ölçeğe uygun şekilde ölçümlenmiş değişkenler arasındaki ilişkinin derecesini belirlemek için Pearson korelasyon katsayısı kullanılır. Bu katsayı r ile gösterilir. r değeri, -1 ile +1 arasında değişen değerler alır. -1 ve +1 değerlerine eşit sonuçlar mükemmel / tam ilişkinin varlığını gösterir.
- Eksi değerler, değişkenler arasındaki ters yönlü ilişkiyi gösterir (biri artarken diğeri azalır).
- Artı değerler, değişkenler arasındaki aynı yönlü ilişkiyi gösterir (biri artarken diğeri de artar).
Eğer iki değişken arasında hiç ilişki yok ise Pearson korelasyon katsayısı 0 (sıfır) değerini alır.
İşlemtablolarında Pearson korelasyon katsayısını hesaplama PEARSON işleviyle gerçekleştirilir.
Yazımı: PEARSON( dizi1;dizi2 )
İşlev yazımındaki parametreler:
- Dizi1: Gözlem değerlerinin bulunduğu aralık, gereklidir.
- Dizi2: Gözlem değerlerinin bulunduğu aralık, gereklidir.
Belirlilik katsayısı , bağımlı değişkenin toplam değişkenliğini, bağımsız değişken veya değişkenlerin açıklama oranını tespit etmek üzere kullanılır. Belirlilik katsayısı Pearson korelasyon katsayısı r’nin karesinin alınması ile hesaplanır. 0 ile 1 arasında değerler alır ve oran olarak ifade edilir. İşlemtablolarında belirlilik katsayısı RKARE işleviyle gerçekleştirilir.
Yazımı: RKARE(bilinen_y’ler;bilinen_x’ler)
İşlev yazımındaki parametreler:
- Bilinen_y’ler: Gözlem değerlerinin bulunduğu aralık, gereklidir.
- Bilinen_x’ler: Gözlem değerlerinin bulunduğu aralık, gereklidir.
Regresyon analizinin konusu, değişkenler arasındaki neden-sonuç ilişkisini matematiksel bir fonksiyonla açıklamak veya ifade etmek işlemidir. Regresyon analizinde iki farklı değişken bulunmaktadır:
- Bağımlı değişken: İlgilenilen değişkendir.
- Bağımsız değişken/değişkenler: Bağımlı değişken üzerinde etkisi bulunan değişken ya da değişkenlerdir.
Eğer bir tane açıklanan (bağımlı) ve bir açıklayıcı (bağımsız) değişken ile ilgileniliyorsa basit regresyon , bir açıklanan (bağımlı) ve birden fazla açıklayıcı değişkenle (bağımsız) ilgileniliyorsa çoklu regresyon söz konusudur. İlgilenilen değişkenlere ilişkin matematiksel ifadeye veya fonksiyona regresyon denklemi denir.
Basit doğrusal regresyon modeli y i = ? + ßx i + ? i olarak yazılır. Burada:
yi : bağımlı değişken y’nin i’inci gözlem değeri,
ßxi : bağımsız değişken x’in i’inci gözlem değeri,
?i : i’inci gözlem için ortalaması 0 ve tüm gözlemler için sabit ? standart sapmalı Normal dağılıma sahip olduğu varsayılan rassal hata,
? ve ß : veri yardımıyla tahmin edilecek, x=0 olduğunda y’nin değeri ? ve x’te meydana gelecek birim değişikliğin y’deki oransal etkisi de ß olmak üzere ana kütle parametreleri,
En küçük kareler analizi bir enküçükleme tekniğidir. Gerçek y değerleri ile tahmin sonucu elde edilen y değerleri arasındaki düşey farkların kareleri toplamının en küçüklenmesi sağlanır. Bu teknik yardımıyla basit doğrusal regresyon modelinde yer alan ana kütle parametreleri ? ve ß için veri yardımıyla a ve b tahminleri belirlenir. Basit doğrusal regresyon modelinde ß regresyon doğrusunun eğimini, ? ise doğrunun y eksenini kesim noktasını gösterir.
İşlemtablolarında ß için veri yardımıyla b tahmini EĞİM işleviyle gerçekleştirilir.
Yazımı: EĞİM ( bilinen_y’ler;bilinen_x’ler )
İşlev yazımındaki parametreler:
- Bilinen_y’ler: Gözlem değerlerinin bulunduğu aralık, gereklidir.
- Bilinen_x’ler: Gözlem değerlerinin bulunduğu aralık, gereklidir.
İşlemtablolarında ? için veri yardımıyla a tahmini KESMENOKTASI işleviyle gerçekleştirilir.
Yazımı: KESMENOKTASI ( bilinen_y’ler;bilinen_x’ler )
İşlev yazımındaki parametreler:
- Bilinen_y’ler: Gözlem değerlerinin bulunduğu aralık, gereklidir.
- Bilinen_x’ler: Gözlem değerlerinin bulunduğu aralık, gereklidir.
İşlemtablolarında regresyon denklemi yardımıyla araştırmacı gözlemlediği herhangi bir x değeri için y’nin alacağı değeri tahminini TAHMİN işleviyle gerçekleştirir.
Yazımı: TAHMİN ( x;bilinen_y’ler;bilinen_x’ler )
İşlev yazımındaki parametreler:
- x: Elde edilen regresyon denkleminde tahmin edilmek istenen veri noktası, gereklidir.
- Bilinen_y’ler: Gözlem değerlerinin bulunduğu aralık, gereklidir.
- Bilinen_x’ler: Gözlem değerlerinin bulunduğu aralık, gereklidir.


