Ünite 3: Karar Ağacı ve Ek Bilgi İle Karar Verme

Karar Ağacı

Karar ağacı, karar vericinin karar verme probleminde ortaya çıkabilecek tüm durumları (senaryoları) bir arada izleyebileceği grafiksel bir yaklaşımdır. Bu bağlamda karar ağacı olası alternatiflerin ve sonuçların şematik gösterimidir. Strateji matrisinin (kitabın 43. Sayfasındaki tablo 3.1.'de gösterildiği gibi) grafiksel gösterimi Karar Ağacı yardımıyla gerçekleştirilir. Karar ağaçları genellikle risk ortamında karar verme durumunda kullanılır. Ancak karar ağacı kullanımı sadece risk ortamı ile sınırlı değildir. Karar ağacının bir dizi temel bileşeni bulunur. Bu bileşenler şunlardır:

Şans düğümleri, karar ağacında daire sembolü ile gösterilir. Şans düğümlerinden çıkan dallar, ortaya çıkış olasılıkları belirli değerleri alabilen olaylar için kullanılmaktadır.

Dal: Düğümlerin birbirine bağlanmasını sağlayan doğrudur. Karar düğümünden sağa doğru çizilen doğrular karar dalları, şans düğümünden sağa doğru çizilen doğrular ise şans dallarıdır. Karar verme problemlerinde karar dalları stratejileri (seçenekler-alternatifler), şans dalları ise doğal durumları (olayları) göstermek için kullanılır. Eğer problemde ilgili şans dalına ait doğal duruma ilişkin olasılık değeri hesaplanmış ise şans dalının üzerine o şans dalının temsil ettiği doğal durumun ortaya çıkma olasılığı yazılır.

Bitiş Noktası: İlgili dal için nihai sonucun belirtildiği kısımdır.

Eğer birden fazla karar verme söz konusu ise, bir şans dalından sonra bir başka karar düğümü yer alabilir. Benzer şekilde karar düğümünü izleyen dallardan bir tanesi de karar düğümü olabilir. Karar ağacı çözümü göstermek için kullanıldığında, her şans düğümünün üzerinde, o şans dalına ulaşmak için seçilmesi gereken karar alternatifi için hesaplanan en iyi beklenen değerler (EBD) yer alacaktır. Eğer bir şans dalını takip eden karar düğümü var ise bu karar düğümü üzerine, ilgili karar problemi sonucunda elde edilen en iyi kararın sonucu (örneğin, en iyi beklenen değer sonucu) yazılmalıdır.

Karar ağaçları temel karar düğümü solda yer almak üzere soldan sağa doğru yönlendirilmiş bir akışta oluşturulur. Karar ağacının çizim işlemleri tamamlandıktan sonra, karar ağacının en sağından başlanarak, ilgili değerler uygun yerlere yerleştirilir. (kitabın 45. sayfasındaki şekil 3.1.'de gösterildiği gibi) Şekil 3.1’de iki adet karar alternatifi ve iki adet doğal durum bulunmaktadır. Şekilde en solda gösterilen kare, bir karar düğümüdür, bu düğümden karar alternatifi sayısı kadar dal sağa doğru yönlendirilir. Bu karar probleminde iki adet karar alternatifi bulunduğu varsayıldığından, iki şans düğümü için iki dal oluşturulmuştur. Karar düğümünden sağa doğru yönlenen iki dalın ucunda bulunan daireler şans düğümleridir. Bu şans düğümlerinin her birinden karar problemindeki doğal durum sayısı kadar dal sağa doğru yönlendirilir. Bu şekilde iki adet doğal durum olduğundan, her bir karar alternatifine ait şans düğümü için iki adet şans dalı bulunmaktadır. Her şans dalı sonunda ise strateji matrisinin sonuç değerlerini barındıran bitiş noktaları yer alır. Strateji matrisinde yer alan s11 sonuç değeri, karar vericinin 1 no’lu karar alternatifini benimsemesi ve birinci doğal durumun ortaya çıkması durumunda elde edilecek kazanç/ maliyet değeridir. Aynı biçimde, diğer sonuç değerleri de strateji tablosundan karar ağacına aktarılır. Başlangıç karar düğümünden bitiş noktalarına kadar izlenen yola senaryo adı verilir. Basit karar ağaçlarında bitiş noktalarında yer alan sonuç sayısı sayılarak problemde kaç tane senaryo olduğu tespit edilebilir. Şekil 3.1’in bitiş noktalarında dört adet değer olduğuna göre, bu problemde karar vericinin karşılaşabileceği dört senaryo vardır.

Karar ağacının sadece bir adet karar düğümü içerdiği ve her karar alternatifi içinde eşit sayıda doğal durum bulunduğu karar ağaçlarına simetrik karar ağacı adı verilir. Karar ağacının simetrik olma özelliği ortadan kalkması durumunda asimetrik karar ağacı (kitabın 46. Sayfasındaki tablo 3.2.'de gösterildiği gibi) oluşmaktadır. Asimetrik karar ağacı sadece bir tane strateji matrisi yardımıyla modellenemez ve çözüme ulaşmak için birden fazla strateji matrisi oluşturulması gerekir. Böyle bir durumda strateji matrisi kullanımının çözüme ulaşmada yaratacağı karmaşıklık, problemle ilgili karar ağacı çizimi yardımıyla en aza indirgenebilir. Karar verici, birbirini takip eden strateji matrisleri ile göremeyeceği olası tüm senaryoları asimetrik karar ağacı yardımıyla bir çırpıda görebilecektir.

Karar ağaçları, çizimleri kolay olan ve karar vericiye en iyi karar alternatifinin seçiminde görsel olarak yardımcı olan grafiklerdir. Karar ağaçları aşırı hesaplamaya gerek kalmadan sınıflama yapar ve hem sürekli, hem de kesikli değişkenler için uygundur. Ancak karar ağaçlarının en büyük dezavantajı, karar alternatifi ve doğal durum sayısının artması durumunda karar ağacının karmaşık bir yapı alabilmesidir.

Karar ağaçları karar düğümü ile başlar ve sonuç değerleri ile tamamlanır. (kitabın 46. Sayfasındaki tablo 3.2.'de gösterildiği gibi) Karar verici karar ağacının çizimini tamamladıktan sonra karar ağacının en sağından karar düğümüne doğru ilerleyerek en iyi sonuca ulaşır. Her şans düğümünde karar verici probleme uygun tekniği kullanarak o şans düğümüne ait en iyi sonucu belirler ve şans düğümü üzerine bu değeri yazar. Karar düğümünden çıkan tüm dallara ilişkin sonuç değerlerinin tamamı hesaplandıktan sonra, ilgili sonuçlardan en iyisini veren karar seçeneği, en iyi seçenek olarak belirlenir. En iyi karar seçeneği ya da stratejisi belirlendikten sonra, elenen karar seçeneklerini temsil eden dallar üzerine yan yana iki paralel çizgi çizilerek bu dalların temsil ettiği karar seçeneklerinin elendiği gösterilir. Bu yapısı ile karar ağaçları, karar problemlerinin çözümünde, tümevarım yöntemiyle çizilme, tümdengelim yöntemi ile çözülme özelliği ile katkı yaparlar.

Karar Vermede Bayes Teoremi

Bayes teoremi temel olarak bir olaya ilişkin bilinen olasılıkların yeni bilgi ışığı altında tekrar gözden geçirilmesi işlemidir. Bayes teoremini açıklamak gerekirse bir problemdeki doğal durumlar; D1, D2, D3, …, Dn, bu doğal durumların ortaya çıkma olasılıkları da P(D1), P(D2), P(D3),…, P(Dn) olsun; x probleme ilişkin bir olay iken, x olayı ortaya çıktığında veya x olayına ilişkin bir sonuç kesin olarak bilindiğinde tanımlanan doğal durumlardan herhangi birinin ortaya çıkması olasılığı;

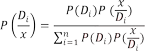
eşitliği yardımıyla hesaplanır. Bu eşitlik Bayes kuralı olarak tanımlanmıştır. Ek bilgi elde edilerek uygulanan Bayes kuralı yardımıyla, doğal durumların ortaya çıkma olasılıklarının yeniden gözden geçirilebilmesi fırsatı yakalanmış olur. P(D _i ) olasılıkları; örneklem bilgisi elde edilmeden ya da ekstra araştırmalar yapılmadan önce doğal durumlar için atanan ilk olasılık değerleridir. Bu olasılıklar geçmiş deneyimlere göre atanmış olabileceği gibi karar vericinin öznel kararları ile de oluşturulmuş olasılıklardır. x olayı probleme ilişkin elde edilen herhangi bir örneklem bilgisini temsil etmektedir. Farklı doğal durumlar için P(D _i /x) olasılıkları ise, x örneklem bilgisi elde edildikten sonra ilgili doğal duruma ilişkin hesaplanan yeni olasılık değerleridir. Bayes kuralında P(D _i ) olasılıkları önsel olasılıklar, P(D _i /x) olasılıkları ise sonsal olasılıklar olarak adlandırılır. Bayes kuralı içerisinde yer alan ve P(D _i /x) biçiminde yazılan olasılıklarsa olabilirlikler olarak adlandırılır. Olabilirlikler herhangi bir doğal durumun ortaya çıkması durumunda x’in herhangi bir sonucunun ortaya çıkması olasılıklarıdır. x’in her bir sonucu için ayrı ayrı hesaplanan olasılıklar ise koşullu olasılıklardır. Bayes kuralı eşitliğininin paydasında yer alan olasılık çarpımı da bileşik olasılık olarak adlandırılır. Paydada yer alan herhangi bir çarpım sonucunun elde edilebilmesi için araştırmacının, hem hangi doğal durumun ortaya çıktığını, hem de bu doğal durumun hangi x sonucuna ulaşıldığını bilmesi gerekir. Dolayısıyla paydada hesaplanan olasılıklar bileşik olasılıklardır. Bileşik olasılıklar, karar verme problemlerinde karar ağacı tanımlamalarında bahsedilen her bir senaryoya karşılık gelmektedir. Bayes kuralına ilişkin çözümler Bayes kuralı eşitliği yardımıyla çözülürken, ortaya çıkabilecek işlem yükü sorunu karar ağacı çözümü yardımıyla azaltılabilir. Bayes kuralı çözümü için oluşturulacak karar ağacı örneği kitabın 52. sayfasında Şekil 3.6’da gibi oluşturulmaktadır. Şekil 3.6’ya göre karar vericinin karşılaşabileceği 3 tane doğal durum vardır. Bu doğal durumlara ilişkin ek bilgi sağlayan x değişkeninin de, 2 adet sonucu olduğu şans dallarından görülmektedir. Karar ağacının bitiş noktalarında, problemde yer alan senaryo sayısı kadar sonuç olduğu hatırlanırsa Şekil 3.6’ya göre toplam 6 senaryo bulunmaktadır. Bu 6 senaryo’dan 3’ü x’in ilk sonucu için, kalan 3’ü ise x’in diğer sonucu için ortaya çıkmaktadır. x’in ilk sonucuna ilişkin ortak olasılıklar Şekil 3.6’daki karar ağacının bitiş noktalarının yukarıdan aşağıya 1, 3 ve 5’inci noktalarında yer almaktadır. Bu üç değer muhtemel bir Bayes kuralı işleminde, Bayes kuralı eşitliğinin sağ tarafındaki payda toplamını oluşturan bileşenlerdir. Bu bileşenlerden hangisi araştırmacının ilgilendiği sonuç ise, o sonuca ilişkin bileşik olasılık değeri de Bayes eşitliğinin sağ tarafındaki pay kısmını oluşturur. Kitabın 52. Sayfasında Tablo 3.6’da yer alan şekilde Bayes olasılığı P (D ₃ | x ₂ ) (x değişkeninin x ₂ sonucunu aldığı bilindiğinde, üçüncü doğal durumun ortaya çıkma olasılığı) ise

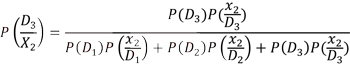
eşitliği yardımıyla hesaplanır. Verilen eşitlik incelendiğinde, paydada yer alan toplama ait bileşenlerin Karar ağacında x2 sonucunu içeren bileşik olasılıklar olan 2. 4. ve 6. bitiş noktalarındaki sonuçlar olduğu görülebilir. Pay’da yer alan değer ise Bayes kuralında sadece üçüncü doğal durum ile ilgilenildiğinden üçüncü doğal duruma ilişkin değerdir. Dolayısıyla karar verici Bayes kuralının uygulanmasının beklendiği problemlerde karar ağacını çizerek istenen değerleri kolaylıkla bulup, hesaplama yapabilir.

Tam Bilginin Beklenen Değeri

Tam bilginin beklenen değeri, hangi doğal durumun ortaya çıkacağının kesinlikle öğrenilmesiyle elde edilebilecek en iyi getiri değeri ile hangi doğal durumun kesinlikle ortaya çıkacağı bilgisi öğrenilmeden önceki en iyi beklenen getiri değeri arasındaki fark olarak tanımlanabilir. Tam bilginin değerini hesaplamak için araştırmacı “her doğal durum için en yüksek getiri değerlerini” tespit eder. Bu değerleri kullanarak strateji matrisi için toplam tam bilgi değerini hesaplar. Tam bilgi olmadan en iyi strateji için beklenen getiri de hesaplanır. Karar verme problemlerinde tam bilginin beklenen değeri (Expected Value of Perfect Information) EVPI kısaltması ile kullanılır. Tam bilginin beklenen değerinin hesaplanması için,

EVPI = [Tam bilgi ile elde edilen getiri] – [Tam bilgi olmadan elde edilen beklenen getiri] eşitliği kullanılır.