Ünite 4: AHP

Analitik Hiyerarşi Süreci

AHP (AHS), Çok kriterli karar problemlerinde seçenekler arasından seçim yapmada nitel ve nicel faktörleri birlikte değerlendirebilen bir tekniktir. AHP (Analytic Hierarchy Process) Thomas L. Saaty tarafından geliştirilmiş, çok kriterli karar problemlerinin modellenmesi ve çözümlenmesinde kullanılan bir tekniktir. AHP’ye Türkçe kaynaklarda, tekniğin adının Türkçe “Analitik Hiyerarşi Süreci” biçimindeki tercümesinden kısaltılarak AHS de denilmektedir. Teknik karar vermede grup veya bireyin önceliklerini dikkate alarak, nicel ve nitel kriterleri birleştirerek değerlendirme olanağı sağlamaktadır.

Analitik hiyerarşi süreci ele alınan problemi hiyerarşik bir yapıya dönüştürür ve ikili karşılaştırmalara dayanır. Bu karşılaştırmalar her bir kriter ve seçenek ikilisi için gerçek ölçüm değerleri kullanılarak veya yargı ve tercihlerin göreli gücünü yansıtan bir ölçek ( Temel Ölçek ) kullanılarak gerçekleştirilir. Karşılaştırma sonucu elde edilen değerler ise ikili karşılaştırma matrisi olarak adlandırılan matrislerle gösterilir. Bu matrisler analiz edildikten sonra, ele alınan iki elemanın ( kriter, seçenek ) hangisinin daha önemli, tercih edilir veya baskın olduğu ortaya konur. Analitik hiyerarşi süreci, problemi çok düzeyli hiyerarşik yapıda ele alır. Karar vericinin, problemi hiyerarşik bir yapıda bileşenlerine ayrıştırmasıyla, problem alt problemlere parçalanmış olur. Bu alt problemlerin çözümünden ise karar probleminin çözümüne ulaşılır.

Hiyerarşik Yapı

Hiyerarşik yapı, problemin ayrıntılı bir biçimde ortaya konması amacıyla oluşturulan ve bir dizi homojen elemandan oluşan katmanlardır. AHS’de hiyerarşik yapı en üst seviyede amaç olmak üzere kriterler (varsa alt kriterler) ve seçeneklerden oluşur. Analitik hiyerarşi sürecinde karar problemi hiyerarşik bir modele dönüştürülür. Hiyerarşik yapı oluşturulurken hiyerarşinin bir seviyesindeki elemanların kendisinden önce gelen bir üst seviyedeki tüm elemanlara göre anlamlı bir şekilde karşılaştırılabilir olup olmadığı göz önünde bulundurulur. Bir anlamda belirli bir seviyedeki elemanlar bir üst seviyedeki eleman veya elemanlarla ilişkilendirilir.

Hiyerarşik yapı amaç, kriterler ve seçeneklerden oluşur. Hiyerarşik yapının oluşturulmasında ilk adım amacın belirlenmesidir. Kriterler ve seçenekler amaca göre şekillenir. Amaç hiyerarşide en üst seviyede yer alır. Amaç belirlenirken neyin başarılmaya çalışıldığı sorusuna cevap aranır. Hiyerarşide amacı izleyen ikinci seviyede kriterler yer alır. Kriterler, amacın başarılmasında katkıda bulunacağı düşünülen faktörlerdir. Gerekli görülmesi durumunda kriterlerin daha alt seviyeleri tanımlanır ve bu seviyelerde yer alan faktörler, alt kriterler olarak isimlendirilir. Alt kriterler de ilgili kriterin başarılmasında etkili olan faktörler olarak ifade edilir. Son olarak hiyerarşinin en alt seviyesinde ise seçenekler yer alır. Analitik hiyerarşi sürecinde en temel hiyerarşi yapısı, amaç, kriterler ve seçenekler olmak üzere 3 seviyeden oluşur. (Kitabın 67. Sayfasında Şekil 4.1.’de gösterildiği gibi) Hiyerarşik yapının tüm bileşenleri birbirleri ile ilişkilidir ve bir bileşendeki değişimin diğer bileşenleri nasıl etkilediği hiyerarşik yapıdan kolayca görülmektedir. Problem hiyerarşik yapıda ifade edilirken kriterlere ilişkin alt kriterlerin tanımlanması durumunda seviye sayısı kullanılan alt kriter seviye sayısına bağlı olarak değişecektir. Alt kriterlerin kullanıldığı hiyerarşik yapı kitabın 67. Sayfasında şekil 4.2.’de yer almaktadır. İhtiyaç duyulan alt kriterlerin düzey sayısına bağlı olarak hiyerarşinin seviye sayısının nasıl farklılaştığı kitabın 67. Sayfasında Şekil 4.2’ de görülmektedir. farklılaştığı kitabın 67. Sayfasında Şekil 4.2’de alt kriter sayısına bağlı olarak 4 seviyeden oluşan bir hiyerarşik yapı örneklenmiştir. Seviye 3’ te yer alan alt kriterlerin herhangi biri için bir düzey daha ayrıştırma yoluna gidilmesi ve alt kriter kullanılması durumunda ise bu kez hiyerarşik yapıda yer alan seviye sayısı 5 olacaktır.

Temel Ölçek

Analitik hiyerarşi sürecinde homojen elamanlar (kriterler, alt kriterler ve seçenekler) ikili olarak karşılaştırılır. Bu karşılaştırmalarda yargılar 1-9 temel ölçeği (kitabın 68. Sayfasında Şekil 4.1.’de gösterildiği gibi kullanılarak sayısallaştırılır.

İkili Karşılaştırmalar Matrisi

İkili karşılaştırmalarda ulaşılan yargıların temel ölçek yardımıyla dönüştürülen sayısal değerleri bir matrise girilerek ikili karşılaştırmalar matrisi elde edilir. İkili karşılaştırmalar amaca göre kriterler (hiyerarşik yapıda alt kriter söz konusu ise kriterlere göre alt kriterlerin) ve ayrıca bu kriterlere bağlı olarak seçenekler için gerçekleştirilmektedir.

Analitik Hiyerarşi Sürecinin Çözüm Aşamaları

Analitik hiyerarşi sürecinin problem çözüm aşamaları üç temel ilke üzerine inşa edilmiştir. Bu ilkeler sırasıyla; ayrıştırma/hiyerarşik yapının geliştirilmesi, tercihlerin ikili karşılaştırılması ve sentezdir.

Ayrıştırma/Hiyerarşik yapının geliştirilmesi aşamasında karar probleminin karmaşık yapısından hiyerarşik homojen kriterler kümesine geçiş gerçekleştirilir. Ayrıştırma aşaması karar probleminin elemanlarının (amaç, kriter, alt kriter, seçenekler) tanımlanması ile başlar. Problemin elemanlarının homojen küme ve alt kümeleri oluşturularak aralarındaki ilişki, hiyerarşik bir yapı ile gösterilir. Hiyerarşik yapı yardımıyla aynı zamanda karar probleminin amaca ulaşabilecek şekilde alt problemlere ayrıştırılması sağlanır. Analitik hiyerarşi sürecinde hiyerarşinin oluşturulması tekniğin ilk adımıdır. Hiyerarşik düzende en tepede amaç yer almaktadır. Amacın altında kararı etkileyecek kriterler bulunur. Kriterlerin, amacı etkileyecek özellikleri varsa kriterler alt kriterlere ayrılır. Hiyerarşinin en alt bölümünde ise seçenekler yer alır.

İkili karşılaştırma, hiyerarşide yer alan elemanların bir üst düzeydeki eleman üzerindeki etkilerinin gücüne göre karşılaştırılmasıdır. İkili karşılaştırma, matrisler yardımıyla yapılır ve seçeneklerin öncelik sıralamasının belirlenmesi amacıyla kullanılır. Karşılaştırmalar hiyerarşik yapıya göre yukarıdan aşağıya doğru gerçekleştirilir. Tekniğin ikinci adımı ikili karşılaştırma matrislerinin oluşturulmasıdır. İkili karşılaştırma matrisleri oluşturulduktan sonra analiz gerçekleştirilir. Bu analizde ikili karşılaştırma matrislerinde yer alan elemanların göreli önem (öncelik) değer vektörü elde edilir. Analitik hiyerarşi sürecinin çözümünün üçüncü adımında her seviyede yer alan elemanların (kriterler, seçenekler) göreli önem değerleri bulunur. w = (w ₁ ,…, w _n )T göreli önem vektörünü elde etmek için önce matriste her bir sütun değeri ayrı ayrı ilgili sütun toplamına bölünerek normalleştirme işlemi yapılır. Daha sonra normalleştirilmiş matriste her bir satırın ortalaması alınır. Bu değerler, karşılaştırması yapılan elemanların göreli önem değerlerini vermektedir. İkili karşılaştırma matrislerinin analiz edilmesi ile farklı ölçüm birimleriyle ifade edilen kriterlerin karşılaştırılması gerçekleştirilmektedir. Yapılan işlemlerle ölçüm birimlerinden arındırılmış göreli önem değerlerine ulaşılır. Bu değerlerin toplamı 1’e eşittir. Bu hesaplamalar ikili karşılaştırmaların yer aldığı matrisin tutarlı olması durumunda geçerli olacaktır.

Tutarlılık oranı karar vericinin ikili karşılaştırmalardaki tutarsızlık düzeyini ortaya koyar. İkili karşılaştırmalarda yargılarda bulunan kişinin değerlendirmede gösterdiği tutarsızlık tutarlılık oranı olarak ifade edilir. Tutarsızlık belirli bir oranın (%10) altında ise kabul edilebilirken bu oranın üzerine çıktığında karar vericiden ikili karşılaştırma yargılarını tekrar gözden geçirmesi istenebilir. Analitik hiyerarşi sürecinde karar vericinin ikili karşılaştırmalarda yapabileceği tutarsızlık; ikili karşılaştırma matrisine ait tutarlılık oranı, tutarlılık indeksinin rassal tutarlılık indeks tablosundan okunan aynı boyuttaki matris için türetilmiş rassal değere oranlanması ile hesaplanmaktadır.

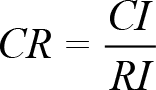
CR: Tutarlılık Oranı

CI: Tutarlılık İndeksi

RI: Rassal Tutarlılık İndeksi (Rassallık göstergesi)

CR formülünün payında yer alan

CI tutarlılık indeksi ise;

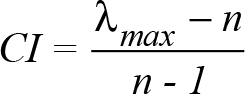formülü ile hesaplanır.

Bu formülde yer alan (?max) değeri de

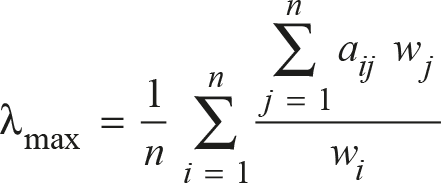
eşitliğinden bulunmaktadır.

Sentez

Analitik hiyerarşi sürecinde sentez çözüm adımlarının sonuncusudur. Sentez; problemin bütünü içinde, amacı gerçekleştirme açısından seçeneklerin bütünsel (global) önem değerinin (ağırlığının) belirlenmesidir. Bu işlem her bir seçenek için; ilgili seçeneğin bir kriterden aldığı göreli önem değeri ile ilgili kriterin göreli önem değerinin çarpımının tüm kriterler için yapılarak çarpımların toplanmasından oluşur. Sentez işlemi ile seçeneklere ilişkin bütünsel önem vektörüne ulaşılır. Elde edilen değerler, karar vericinin seçenekleri bu değerlere göre sıralamasına olanak verir. Böylelikle seçeneklerin amaca yaptıkları katkı dikkate alınarak seçenekler hakkında karar verilmesi mümkün olur. Seçenekler için bütünsel önem değerlerinin hesaplanmasında aşağıdaki formülden yararlanılır;

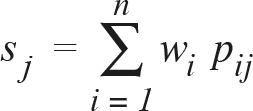
formülde; s _j : j’ inci seçeneği (j = 1, 2, …, m)

w _i : i’inci kriterin ağırlığı (i = 1, 2, …, n),

p _ij : j’ inci seçeneğin i’inci kritere göre ağırlığı (i = 1, 2, …, n; j = 1, 2, …, m) göstermektedir.

Hiyerarşik yapıda kriterlerle birlikte alt kriterler tanımlanmış ise bu durumda seçeneklere ilişkin bütünsel önem değerleri elde edilirken öncelikle alt kriterlerin göreli önem değerleri belirlenir. Alt kriterlerin göreli önem değerleri bağlı bulundukları kritere göre ikili karşılaştırmalardan oluşan matrislerin çözümlenmesiyle elde edilir. Alt kriterlerin göreli önem değerleri; aynı zamanda bağlı olduğu kriter için kısmi (lokal) önem değerini, amaç üzerindeki önem değeri ise bütünsel (global) önem değerini belirtir.

Analitik Hiyerarşi Sürecinin Uygulama Alanları

Analitik hiyerarşi süreci karar verme teknikleri içinde yaygın kullanımı olan bir tekniktir. Tekniğin sağlık, savunma, proje planlama, tahmin, pazarlama, yeni ürün fiyat belirleme, politika değerlendirme, finans ve yönetim gibi pek çok alanda uygulaması görülmektedir. Tekniğin uygulandığı problem türlerinden başlıcaları aşağıda sıralanmıştır.

• Seçim problemleri: Bir dizi seçenek arasından birinin seçilmesi.
• Önceliklendirme/değerlendirme problemleri: Bir dizi seçeneğin göreceli değerinin belirlenmesi.
• Kaynak dağıtım problemleri: Seçeneklerin en iyi alternatif kombinasyonunun bulunması.
• Kıyaslama: Süreçlerin veya sistemlerin bilinen süreç ve sistemlerle karşılaştırılması.

Analitik hiyerarşi sürecinde karar vermek için analitikmatematiksel ve mantıksal akıl yürütme gerçekleştirilir. Teknik karar vericinin problemi mantıksal bir zeminde çözümünü olanaklı hale getirmekle birlikte karar vericinin sezgilerini içgüdülerini başkaları tarafından sorgulanabilir ve açıklanabilir sayılara dönüştürmesine yardımcı olmaktadır.

Analitik hiyerarşi sürecinde problem hiyerarşik bir yapıda ele alınmaktadır. İnsana doğal gelen hiyerarşik ayrıştırma, karar vericinin problem çözümünde karşılaştığı problemi tek başına ele alması yerine alt problemlere bölmesidir.

Analitik hiyerarşi süreci karar verme için bir süreç tanımlamaktadır. Teknik bireylere ve gruplara karar verme için bir dizi işlem tanımlamaktadır. Özellikle grup kararı ile ortak karara ulaşılırken, kararın geliştirilme ihtiyacı söz konusu olmaktadır. Grup kararının verilmesinde karar vericilerin girdilerinin birleştirilmesi ve gözden geçirilmesi gerekmektedir.

Bir hiyerarşik yapıda kriterlerin ve/veya alt kriterlerin sayısı çok olması çok sayıda ikili karşılaştırma gerektirecek ve tekniğin uygulanmasını zorlaştıracaktır. Bu tür problemlerde karşılaştırmalar için gereken süre artacaktır. Daha doğru sonuçlara ulaşmak amacıyla değerlendirme süreleri dikkate alınarak sorulara ilişkin cevapların alınması işlemi için birden fazla oturum düzenlenmesi yoluna başvurulabilir. Tekniğin uygulanmasında bir kritere göre seçeneklerin değerlendirilmesi aşamasında bazı durumlarda gerçek değerlerin bilinmesi söz konusudur. Bu değerlerin bilinmesine rağmen analizi gerçekleştiren kişi bu değerlerin yerine temel ölçekten yararlanarak seçeneklerin karşılaştırılması yoluna gidebilir.