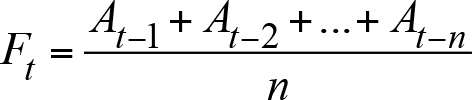Ünite 3: Lojistik Yönetiminde Talep Tahmini

Tahminin Lojistik Planlamada Stratejik Rolü

Lojistik planlama, tahminlere ve hedeflere dayanan sonuç olarak ortaya çıkar. Tahmin, lojistik şirketlerin faaliyet alanları içerisinde önemli rol oynayabileceği için stratejik yönetim karar alma faaliyetlerin ayrılmaz bir parçasıdır. Lojistik şirketleri planlama yaparken kısa, orta ve uzun vadeli tahminlere ihtiyaç duyar. Lojistik planlamada stratejik orta vadeli tahminler genellikle hammadde ihtiyacını belirlemek, geçici personel istihdamı, makine ve teçhizat satın alımı gibi faaliyetler için gelecekteki kaynak gereksinimini belirlemede kullanılır. Uzun vadeli planlamalar içinse hedef pazara giriş ve pazardan ne zaman çıkılacağı gibi, çevresel faktörlerin tahmininde kullanılmaktadır.

Kısa vadeli stratejik planlamada günlük olarak gerekli olan tahminlerin de yapılması gerekmektedir. Günlük çıkış yapacak kamyon, tır ya da herhangi bir sevkiyat aracı sayısı planlamasında günlük talebe, ulaşılacak mesafeye, yük miktarına göre tahminleme yöntemleriyle planlama yapmak gerekmektedir. Bu tür tahminler görece kısa vadede olup taktiksel tahmin olarak adlandırılır. En çok kullanılan tahmin olarak lojistik şirketlerinin kullandığı taktiksel planlamanın içinde yer alır. Müşteri beklentilerini ve hizmetin iyileştirilmesinde ilgili diğer kriterleri karşılayabileceğimizi temin etmek için önemlidir.

Talep tahminin yapılacağı ürün grubuna ait öngörüler strateji belirlenmesinde önemlidir. Bu tahminler genellikle üretim süreci tasarımı, hizmet süreci tasarımı, konum ve dağıtım tasarımı, kaynak kullanım, satış planlaması ve operasyonel planlama ile ilgili tahminler yapar. Bunların hepsi talebin stratejik olarak nasıl karşılanacağı ile ilgili orta ve uzun vadeli kararları içerir.

Tahmin Verisi ve Yöntemleri

Uygun tahmin yöntemi büyük ölçüde hangi verinin mevcut olduğuna bağlıdır. Kullanılabilir veri yoksa veya mevcut veriler tahminlerle ilgili değilse nitel tahmin yöntemleri kullanılmalıdır. Tarihsel verileri kullanmadan iyi tahminler elde etmek için iyi geliştirilmiş sezgisel yaklaşımlar gereklidir.

Nitel Tahmin Yöntemleri

Nitel yöntemlerin kullanıldığı tahminleme teknikleri genellikle uzmanların bilgisinden yararlanır ve çok fazla yargı gerektirir. Lojistik planlama ve modellemede en çok kullanılan nitel tahmin yöntemlerinden bazıları şunlardır:

Uzman görüşü: Anlamlı öngörüler yapmak için uzmanların görüşlerinden, fikir ve tecrübelerinden yararlanılır. Bu tür tahminler istatistiksel veriye ihtiyaç duymaz dolayısıyla ölçülebilir verinin olmadığı durumlarda kullanılır. Bu yöntem, uygulama açısından kolay ve hızlıdır. Uzman görüşü, genellikle tahmin sonucunu beklentilerine göre değiştirir.

Pazar araştırması: Bir lojistik firmasının talep tahminini sağlayacak pazar araştırması yapması mümkündür. Bu yöntem firma çalışanları ya da pazar araştırma şirketleri tarafından yapılabilir. Bu araştırmalar telefon, anket veya kişisel görüşmeyi içeren çalışmaları içerebilir.

Odak grupları: Çok sık tercih edilen nitel tahmin yöntemlerinden biridir. İlgili konu ile lojistik yöneticileri beş ila on kişi arasında değişen konuya hâkim fikir öne sürebilecek gruplar oluşturur. Genellikle katılımcılar arasında marka, ürün, slogan, tasarım ve ilgili kavramları algılamaları ile ilgili sorular soran bir moderatör vardır.

Tarihsel analoji: Mevcut ürüne benzer bir ürünün satış geçmişine benzer karşılaştırılabilecek bir ürünün satış geçmişinin gelecekteki satışları tahmin etmek için incelendiği bir tahmin yöntemidir. Yeni bir ürün veya ürün grubu için talebin tahmin edilmesi için kullanılır.

Delfi metodu: Nitelikli uzman bir grubun pazar eğilimini analiz ederek kararların birleştirildiği tahmin yönetimidir. Uzmanların oluşturduğu tahmin grubudur. Bu grup iki veya daha fazla turda tahmin yapar. Tahmin için ilgili fikirler, öngörüler yazılı ve kapalı bir şekilde toplanır ve sonunda bu tahminler birleştirilerek tek tahmin haline getirilir. Daha sonrada uzmanlara geri bildirim olarak sunulur. İkinci turda katılımcıların görüşleri tekrar alınarak yeniden tahmin yapmaları istenir. İkinci turda ilk turdan farklı görüşler ortaya çıkabilir. Aynı şekilde tüm tahminler birleştirilerek yeni tahmin ortaya çıkar ve tüm katılımcılara duyurulur. Bu döngü uzman grubu tek bir kararda birleşinceye kadar devam eder.

Panel fikir birliği yöntemi: Bu yöntem, bir işletmenin üyelerinin tahminlerini belirlemek için tüm düzeylerde çalışanları bir araya getirir. Tüm katılımcıların fikirlerini beyan etmelerini sağlayacak açık bir süreçtir. Genellikle örgütün üst düzey yöneticileri ile alt seviyesinden çalışanları içerdiğinden süreç içerisinde baskı olabilir.

Nicel Tahmin Yöntemleri

Tahmin, matematiksel modellemeye dayanır. Nicel yöntemleri üç sınıfa ayırabiliriz. Bunlar zaman serileri, nedensel ilişkiler ve benzetimdir. Bu yöntemlerin mantığı geçmiş verilerden yararlanarak, onları kullanarak tahmin yapmaktır. Geçmiş verinin yapısında trend, sezonsallık ve döngüsellik gibi farklı bileşenler olabilir. Doğrusal regresyon modeli zaman serilerinin modellenmesinde kullanıldığı gibi nedensel ilişkinin açıklanmasında da kullanılır. Simülasyon modelleri ise tahmin edilecek modelin istatistiki veriler aracılığıyla benzetilmesi olarak bir dizi varsayımı değerlendirir.

Çoğu durumda ürün veya hizmete yönelik talep tahmini farklı bileşenlere ayrılabilir. Bunlar dönem için ortalama talep, trend, sezonsallık, döngüsellik, rasgele değişim ve otokorelasyondur. Kitabınızın 53. sayfasındaki Şekil 3.2 süre boyunca talebi; ortalama talep, mevsimsel bileşenleri ve yumuşatılmış talep eğrisi etrafındaki rasgeleliği göstermektedir. Dönem için ortama talep verinin bir ortalama etrafında hareket ettiği trendin veya mevsimselliğin görülmediği talebi gösterir. Trend, pazarın belirli bir süre boyunca izlediği genel yöndür. Trendler yükseliş trendi ve aşağı yönlü piyasalarla ilgili olarak aşağı ve yukarı yönlü olabilir. Bir yönün bir trend olarak kabul edilmesi için belirlenmiş minimum bir süre olmamakla birlikte, yön ne kadar uzun tutulursa Trend o kadar belirgin olur. Sezonsallık, verinin her takvim yılında tekrarlanan düzenli ve öngörülebilir değişiklik sergilediği bir zaman dizisinin karakteristiğidir. Bir yıllık, aylık, haftalık hatta günlük bir süre içinde tekrarlayan veya tekrar eden herhangi bir öngörülebilir dalgalanma veya desenin sezonsal olduğu varsayılır. Döngüsellik, veri sabit bir frekansa sahip olmayarak yükselip indiğinde bir döngü oluşturur. Bu dalgalanmalar genellikle ekonomik koşullardan kaynaklanır ve genellikle “iş döngüsü” ile ilişkilidir. Bu dalgalanmaların süresi genellikle 5-10 yıl arasındadır. Rastgele değişikliklere şans olayları neden olur. İstatistik açısından veri; ortalama, trend, sezonsallık, döngüsellik ve otokorelatiflik ile açıklanır. Bunun dışında kalan talep açıklanamayan kısımdır. Bu geri kalanın nedenini tespit edemezsek bunun rastgele bir şans olduğu varsayılır. Birçok kişi döngüsel veri ile mevsimsel veriyi karıştırır, ancak bunlar çok farklıdır. Dalgalanmalar sabit bir frekansta değilse bunlar döngüseldir; sıklık değişmiyorsa ve takvimin bazı yönleriyle ilişkiliyse desen mevsimsel olur. Genel olarak, döngülerin ortalama uzunluğu mevsimsel bir desenin uzunluğundan daha uzundur ve döngülerin büyüklükleri mevsimsel desenin büyüklüklerinden daha değişken olma durumundadır.

Zaman Serisi Tahmin Modelleri

Zaman serisi tahmin modelleri geçmiş verileri kullanarak geleceği tahmin etmeye çalışır. Lojistik planlama işlevleri üç tahmin dönemine kısa-orta-uzun ihtiyaç duyar, çünkü her biri doğrudan farklı bir iş işlevini etkiler ve daha da önemlisi orta ve uzun vadeli tahminler lojistik planlama süreci için kritik öneme sahiptir. Kısa dönem için yapılan tahinin süresi bir yıla kadar olmakla birlikte genellikle üç ay veya daha az süreyle kullanılır. Kısa dönem tahminleri satın alma, istihdam, üretim planlama, çizelgeleme ve benzeri planlamamaları yapmak için kullanılır. Orta dönem tahminler üç ay ile üç yıla kadar olan zarfında kullanılır. Orta dönem tahminler üretim planlaması, satış planlama, finans, bütçeleme ve farklı işletme planlamaları için kullanılır. Uzun dönem tahmini ise üç yıl ve daha uzun bir süre için yapılır. Yeni ürün, sermaye değişikliği, tesis genişletme, yer seçimi, ve araştırma-geliştirme için kullanılır. Bu dönemler için uygulanacak tahmin modelleri kitabınızın 55. sayfasındaki Tablo 3.1’de gösterilmiştir.

Hareketli Ortalama

Bu yöntem, talep modeli oldukça düz ve yatay tipte olduğunda iyi sonuçlar verir. Bu hareketli ortalama yöntemi, ortalamanın oluşturulmasında kullanılacak en güncel taleplerin sayısını belirten n parametresini gerektirir. Tarih taleplerinin her birine (x ₁ , ..., x _n ) ortalamanın hesaplanmasında eşit ağırlık verilir. Ortalama, gelecek aylar için tahmin edilmiş olur. Dönem uzunluğu tahminin hangi amaçla kullanılacağına bağlıdır. Hareketli ortalama için uygulanan formül şu şekildedir:

Bu formülde kullandığımız;

F t : t dönemine ait tahmin değeri

n: Ortalamanın alınacağı dönem sayısı

At : t dönemine ait gerçekleşmiş talep

Ağırlıklı Hareketli Ortalama

Ağırlıklı hareketli ortalama, daha yeni verilerin eski verilere göre daha farklı önem verilerek belli sayıda geçmiş verilerle yapılan bir tahmin metodudur. Hareketli ortalama her bir bileşenine eşit önem verirken ağırlıklı hareketli ortalama tüm ağırlıkların toplamının 1’e eşit olması koşuluyla her bir öğeye ağırlıkların atanmasına izin verir. Hareketli ortalamada verdiğimiz örnek üzerinden gidersek 4 dönemlik tahmin için yapacağımız ağırlıklandırmada tahmin edilecek aydan önceki gerçekleşmiş talebin %40’ı ve sırasıyla %30’u, %20’si ve %10’u alınabilir. Buradaki amaç son gerçek talebe yüksek ağırlık vererek tahmin edilecek aya daha yakın olan değeri önemli kılmaktır. Bir önceki örnekte uygularsak modelimiz şu şekilde olur:

F _t = w ₁ A _t-1 +w ₂ A _t-2 +...+w _n A _t-n

Burada;

w _n : t-n dönemde oluşan gerçek talebe verilen ağırlık yüzdesidir. Tüm ağırlıkların toplamı 1 olmalıdır.

Üstel Düzeltme

Üstel düzeltme, en son gözlemlere daha fazla ağırlık verildiği ve gözlemler geçmişte kaldıkça ağırlığın azaldığı önceki gözlemlerin ağırlıklı ortalamasını kullanır. Basit üstel düzeltme yöntemleri için tahmin, bir düzeltme parametresi olarak adlandırılan geçmiş değerlerin göreli ağırlıklarla çarpılmasıyla hesaplanır. Üstel düzeltme yöntemine her yeni veri dönemi eklendiğinde en eski olan gözlem çıkarılır ve yeni tahmin hesaplanır. Üstel düzeltme yöntemi tarihi verilerin hareketli ortalaması olarak görülebilir. Üstel düzeltme metodu, her bir geçmiş dönem için üstel olarak (1 - ?) azalan ağırlıkların kullanıldığı zaman serisi tahmin tekniğidir. Üstel düzeltme yönteminde, geleceği tahmin etmek için yalnızca üç veri gerekir: en son tahmin, o tahmin dönemi için gerçekleşen gerçek talep ve bir yumuşatma sabit alfa (?). Düzeltme sabiti, düzeltme düzeyini ve tahmin ile gerçek olaylar arasındaki farklılıklara bağlıdır. Üstel düzeltme sabiti gerçek verideki değişime göre denenerek ve tahmin hatası hesaplanarak revize edilir. Üstel düzeltme yönteminin modeli şu şekildedir:

F _t =F _t-1 + ? (A _t-1 -F _t-1 )

Burada;

F _t : t dönemine ait tahmin değeri,

F _t-1 : t döneminden önceki döneme ait tahmin değeri,

A _t-1 : t döneminden önceki döneme ait gerçekleşen gerçek talep değeri, ?: düzeltme katsayısı, 0 < ?

Trend Eklemeli Üstel Düzeltme

Deseni takip edecek şekilde tasarlanmış trend eklemeli üstel düzeltme tahmin modeli bu açığı kapatmak üzere tasarlanmıştır. Üstel düzeltme tahminlerine trend düzeltmesi de eklenerek tahmin verisi ayarlanabilir. Bunun için ? düzeltme katsayısının yanında ß trend düzeltme katsayısı eklenir. Alfa ve beta, gerçek ile tahmin arasında oluşan hatanın etkisini azaltır. Hem alfa hem de beta dahil edilmezse eğilim hatalara aşırı tepki verir. Trend denkleminin devam edebilmesi için, ilk kez kullanıldığında trend değeri manuel olarak girilmelidir. Bu ilk trend değeri, gözlemlenmiş geçmiş verilere dayanan bilinçli bir tahmin veya hesaplama olabilir. Beta değerleri de alfa değerleri gibi 0 ile 1 arasında değer alır. Beta değeri yine alfa değeri gibi deneme yanılma yoluyla en düşük hata değerini veren olarak bulunur. Trend eklemeli üstel düzeltme modeli iki bölümden oluşur birincisi üstel olarak düzeltilmiş tahmin Ft ikincisi ise üstel olarak düzeltilmiş trend T _t ’dir. Trend eklemeli üstel düzeltme FIT _t bu iki bölümün toplamı olarak bulunur. Trend eklemeli üstel düzeltme modelinin formülü şu şekildedir:

FIT _t =F _t +T _t

T _t = ß (F _t –F _t-1 ) + (1– ß)Tt _-1

F _t =F _t-1 + ? (A _t-1 – F _t-1 )

Burada T _t : t dönemine ait trend değeri ß: trend için düzeltme katsayısı, 0 < ß

Sezonsallık (Mevsimsellik)

Sezonsal desen, talepte tekrarlayan artış ve azalmayı gösterir. Zaman serisi verilerinde sezonsallık düzenli aralıklarla meydana gelen değişimlerin varlığına işaret eder. Sezonsal değişim sezonsal indeks olarak bilinen bir indeksle hesaplanır. Gerçek bir gözlemin sezonsal bir varyasyon yoksa ne olacağına ilişkin olarak karşılaştırılması için kullanılabilecek bir ortalamayı ifade eder. Her bir dönemin talebi toplam talebe bölünerek hesaplanır:

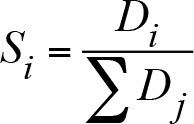
Bulunan sezonsal indeks 0 ile 1 arasında olmalıdır. Bu sezonsal indeksler, her mevsim için düzeltilmiş tahminler vermek üzere yıllık öngörülen talep ile çarpılmaktadır.

Doğrusal Regresyon

Doğrusal regresyon, gözlemlenen verilere doğrusal bir denklem yerleştirerek iki değişken arasındaki ilişkiyi modellemeye çalışır. Bir değişkenin açıklayıcı bir değişken olduğu, diğerinin bağımlı bir değişken olduğu düşünülmektedir. İlişki genellikle gözlemlenen verilerden geliştirilir. Verilerin doğrusal görünüp görünmediğini veya verilerin en azından bir kısmının doğrusal olup olmadığını görmek için önce veriler çizilmelidir. Doğrusal regresyon, değişkenler arasındaki ilişkinin düz bir çizgi oluşturduğu özel regresyon sınıfını ifade eder. Doğrusal regresyon çizgisi Y= a + b _t biçimindedir, burada Y çözdüğümüz bağımlı değişkenin değeridir, a Y kesişimidir, b eğimdir ve t , zaman periyodu için bir indekstir. Regresyon, iki veya daha fazla ilişkili değişken arasındaki fonksiyonel bir ilişki olarak tanımlanabilir. Doğrusal regresyon için bu fonksiyon doğrusaldır. Doğrusal regresyon, büyük olayların ve toplam planlamanın uzun vadeli tahmininde faydalıdır. Doğrusal regresyon hem zaman serisi tahmini hem de nedensel ilişki tahmini için kullanılır. Doğrusal trend çizgisi bağımlı değişken ile bağımsız değişken arasındaki ilişkiyi göstermek için kullanıyoruz. Burada bağımsız değişken olarak zaman serileri bağımlı değişken olarak da tahmin edilecek değerler kullanılır. Eğer, hassas bir istatistiksel metot ile bir trend doğrusu oluşturursak en küçük kareler metodunu uygulayabiliriz. Bu metot, gerçek gözlemlerin trend doğrusundan sapmalarının ya da dikey farkların karelerinin toplamlarını minimize eden düz bir doğru oluşturur. En küçük kareler doğrusunun denklemi ve uygulaması şu şekildedir:

y = a+b _x

Burada;

a = y-ekseni kesişimi

b = regresyon doğrusunun eğimi

x = bağımsız değişken değeri olarak zaman periyodu

y = x değerinin gözlem aralığında tahmin edilecek değer

İlişkisel Tahmin Metotları

Regresyon doğrusunun bir de ilişkisel tahmin metodu olarak kullanılması söz konusudur. Tahmin için regresyon analizi zaman serisi analizinde olduğu gibi modellenir fakat tahmin edilen miktarla ilişkili birkaç değişkeni dikkate alır. İlişkili değerler bulunduktan sonra istatistiksel bir model kurulur ve trend projeksiyonunda yer verilen en küçük kareler metodu kullanılır.

y = a+b _x

burada;

a = y-ekseni kesişimi

b = regresyon doğrusunun eğimi

x = bağımsız değişken değeri

y = tahmin edilecek bağımlı değişkenin değeri şeklinde ifade edilir.

İlişkisel tahmin modellerinde amaç, kullanılan bağımlı ve bağımsız değişkenler arasında ne tür bir ilişkinin olduğunun tespit edilmesidir. İki değişken arasındaki ilişkiyi değerlendirmek için korelasyon katsayısı hesaplanır Korelasyon katsayısı: İki değişken arasındaki ilişkinin açıklamasıdır. “r” ile gösterilir. –1< r < 1 arasında değer alır.

Tahmin Doğruluğu

Tahminler hiçbir zaman tam sonucu vermez. Bunun yerine en yakın sonucu bulmaya çalışırız. Gerçek veri ile tahmin değeri arasındaki farka tahmin hatası denir. Şimdiye kadar gördüğümüz nicel tahmin modellerinin hangisinin veri setimiz için daha uygun olduğuna bakmamıştık. Tahmin hatasını ölçmek için gerçek veri ile tahmin edilen veri arasındaki farka bakılır.

e _t =A _t –F _t

burada

e _t : döneminde oluşan tahmin hata değerini verir.

Tahmin hatasının büyük olduğu durumlarda başka metotlar denenir ya da metot üzerinde gerekli düzeltmeler yapılır. Tahmin hatasını ölçmek için farklı ölçümler vardır. En çok kullanılan tahmin hatalarından bazıları şunlardır; ortalama mutlak sapma, ortalama kareler hatası, ortalama mutlak yüzde hatadır.

Ortalama Mutlak Sapma

En çok kullanılan tahmin hatası ölçüm yöntemlerinden biridir. Ortalama mutlak sapma (OMS), gerçek veri ile tahmin verisi arasındaki farkların mutlak ortalaması olarak bulunur. Bu değer tek tek tahmin hatalarının mutlak değerlerinin toplamının period sayısına bölünmesiyle elde edilir.

Ortalama Kareler Hatası

Bu yöntem de ortalama mutlak sapma yöntemine benzer fakat burada mutlak değer almak yerine tahmin hatasının karesi alınarak bulunur. Tahmin hatalarının karelerinin ortalaması ortalama kareler hatasını (OKH) verir. Bu yöntemde ortalama kareler alındığı için ortalama kareler hatası büyük değerler alır.

Ortalama Mutlak Yüzdelik Hata

Ortalama mutlak sapma ve ortalama kareler hatasına göre ortalama tahmin hatasını yüzdelik olarak hesaplayan bir yöntemdir. Ortalama mutlak yüzdelik hata (OMYH) gerçek değerin yüzdesi olarak ifade edilir. Yüzdelik değer olarak tahmin doğruluğu hesaplandığı için belki en kolay ölçüm yöntemidir. Örneğin OMYH değerinin % 4,5 olduğu bir sonuç yapılan tahmin hatasının yüzdelik açıdan değerlendirmesini vermiş olur.

Yüzdelik değer olarak tahmin doğruluğu hesaplandığı için belki en kolay ölçüm yöntemidir. Örneğin OMYH değerinin % 4,5 olduğu bir sonuç yapılan tahmin hatasının yüzdelik açıdan değerlendirmesini vermiş olur.