Ünite 6: Çağdaş Mantık

Çağdaş Mantığın Doğuşu

Aristoteles mantığı yüzyıllar boyunca egemen mantık sistemini oluşturmuştur. Bu etki öylesine güçlüdür ki Aristoteles mantığına eleştirilerin bazen açıkça aşağılamaya kadar vardığı Rönesans sonrası dönemde bile pek çok mantıkçı Aristoteles mantığının çerçevesi dışına çıkmayı başaramamış, bilim yöntemi hakkında genel kurallar ileri sürmek dışında onun ilkelerini tekrarlamışlardır.

Bu durum ancak 19. yüzyılın sonundan başlayarak çağdaş mantık sistemlerinin ortaya çıkmasıyla değişmiştir. Bu dönemde mantık çalışmalarının artışına yol açan en önemli etken matematiğin temelleriyle ilgili tartışmalardır.

20. ve 21 yüzyılda mantık sadece matematikle değil, yeni ortaya çıkan kuramsal dilbilim, kuramsal bilgisayar bilimi gibi araştırma alanlarıyla da etkileşimli olarak ilerlemiştir. Bu alanlarla da mantığın ilişkisi çift yönlüdür.

Son iki yüzyılda mantıkta dikkat çekici bir olgu, bu dönemde bir arada varolan mantık sistemlerinin çeşitliliğidir. “ Birinci basamak niceleme mantığı ” ya da “ birinci basamak yüklem mantığı ” olarak adlandırılan ( bizim kısaca “niceleme mantığı” diyeceğimiz) mantık sistemi bugün felsefe ve matematik programlarında temel mantık sistemi olarak öğretilmektedir.

Frege’nin Mantıkçı Matematik Görüşü

Alman matematikçi Gottlob Frege (8 Kasım 1848-26 Temmuz 1925) çağdaş mantığın kurucusudur.

Frege geometri doğruları için Kantçı tutumu kabul etmiştir. Aritmetiğe gelince, çalışmalarının son dönemine kadar aritmetik doğrularının analitik doğrular olduğunu savunmuştur. Frege için bir doğru önermenin analitik olması, o önermenin tanımlar ve mantıksal çıkarım kuralları ile elde edilebilmesi demektir. Dolayısıyla Frege tüm aritmetik önermelerinin tanımlardan ve sadece genel mantıksal çıkarım kurallarına başvurarak elde edilebileceğini savunmaktadır. Dahası, aritmetiğin başlangıç noktasını oluşturan tanımlar da sadece mantık kavramlarına yer veren tanımlar olacak şekilde seçilebilir. Frege’nin “mantıkçılık” (ing. logicism) olarak adlandırılan, sıklıkla aritmetiğin mantığa indirgenmesi biçiminde de dile getirilen programının ana hatları bunlardır.

Frege’nin Mantık Sistemi

Frege ne geleneksel mantığın (Aristoteles mantığı) ne de döneminde yaygın kabul gören mantık sistemi olan Boole mantığının mantıkçı programını gerçekleştirmek bakımından yeterli olmadığı sonucuna varmıştır. Frege’nin Boole mantığına eleştirileri şunlardır:

1. Matematiksel gösterimi matematikteki olağan anlamlan ile bağdaşmayan biçimde yeniden kullanmakta, böylece onun matematikteki kanıtlamaları çokanlamlılıktan uzak biçimde temsil etmesine bir engel oluşturmaktadır.
2. İçerdiği ikili yorumlamalarla önerme eklemli ve kategorik/nicelemeli bileşenlerini ayrıştırmakta ve böylece, her iki türden adımlan içeren çıkarımlann temsilini olanaksız kılmaktadır ve
3. Başka kimi eklemeler olmadan, Boole mantığı (örneğin, “Her insan bir kenti sever” önermesi gibi) iç içe nicelemeli önermeleri ele alamaz. (Klement, 2010. s. 862)

Bu düşünceyle, Frege mantıkçı programının ilk adımını gerek duyduğu bir mantık sistemi oluşturmaya girişerek atmıştır. Bu çabasının ilk ürünü 1879 yılında yayımlanan Beggriffschrift (Kavram Yazısı) başlıklı çalışmasıdır.Gerçekleştirmeyi istediği amaç bakımından yeterli olmasa da Frege Beggriffschrift de önermeler mantığının ve birinci basamak niceleme mantığının ilk tam belitsel sistemini ortaya koymayı başarmıştır.

Begriffsschrift’in alt başlığı şudur: “ Aritmetiğin Dilini Örnek alan bir Salt Düşünce Dili ”. Bir salt düşünce dili olması mantığın evrensel karakterini belirtmektedir. Frege’nin de kabul ettiği evrenselci mantık anlayışına göre mantık konu bağımsızdır ve bu sayede her konuya uygulanabilir.

Frege Begriffsschrift’deki mantık dilini aritmetik terimlerinin fonksiyon-argüman yapısını genelleştirerek geliştirir. Aritmetikteki fonksiyon sembollerinin özelliği tek başına tam bir deyim oluşturamamalarıdır: “+” tek başına tamamlanmış bir deyim değildir yani, Frege’nin deyişiyle doymamış bir deyimdir.

Beggriffschrift sistemi sayı kavramını Frege’nin istediği gibi, mantık kavramlarına başvurarak tanımlamaya yeterli olmadığından Frege daha sonra iki cilt hâlinde yayımlanan Grundgesetze başlıklı bir çalışma ile mantık sistemini genişletmiş, ancak meslektaşı Betrand Russell’ın bir mektupla Frege’ye bildirdiği gibi, bu genişletme Frege’nin mantık sistemini tutarsız hâle getirmiştir.

Çağdaş Mantığın Gelişmesi ve Yaygınlaşması

Frege’nin kurucusu olduğunu söylediğimiz çağdaş mantık bugüne değin değişimini ve çeşitlenmesini sürdürmektedir. Bu sırada mantıkçılar mantığın sınırlarına yönelik felsefi düşüncelere de yol açan sonuçlara ulaşmıştır.

Russell’ın Çalışması

İngiliz felsefeci Bertrand Russell (1872-1970) 20. yüzyılın en etkili düşünürlerinden biridir. Uzun meslek yaşamının büyük kısmını çok farklı konularda etkin bir biçimde çalışmayla geçirmiştir. Bunun önemli bir bölümünü de mantık, mantık felsefesi, matematik felsefesi ve dil felsefesi konularındaki çalışmaları oluşturmaktadır.

Russell’ın mantık ve mantık felsefesi ile ilgili çalışmaları arasında en önemlisi Amerikalı matematikçi ve felsefeci Alfred North Whitehead (1861-1947) ile birlikte yazıp hacimli üç cilt hâlinde yayımladıkları Principia Mathematica’dır (Matematiğin İlkeleri).

Russell’da, Frege gibi, mantıkçı bir görüş benimsemekte ve “arı matematiğin tümünün arı mantık ilkelerinden çıktığını ve mantık terimleriyle tanımlanabilen kavramlara başvurduğunu” savunmaktadır.

Russell’ın mantık görüşünü izleyebilmek bakımından önemli diğer eserleri Matematiğin İlkeleri (1903), Matematiksel Felsefeye Giriş (1919) kitapları ile 1908 yılında yayınlanan “ Tipler Kuramı Üzerine Kurulmuş Olarak Matematiksel Mantık ” başlıklı makalesidir.

Russell Matematiğin İlkeleri üzerine çalışırken her özelliğin bir küme belirlediği varsayımına dayanan naif küme kuramının bir çatışkıya yol açtığını fark etmiştir.

Gerçekten, eğer her bir özellik için, o özelliği taşıyan nesneler topluluğunun bir küme oluşturduğunu kabul edersek kendi kendisinin elemanı olmayan kümelerden oluşan topluluğu da bir küme saymamız gerekir.

Russell kümesi olarak adlandıracağımız bu kümeyi küme kuramının sembolik dilinde {x: x ? x} biçiminde gösterebiliriz. Bu tanıma göre, her küme için;

1. Eğer o küme kendisinin elemanı değil ise Russell kümesinin bir elemanıdır ve
2. Eğer küme Russell kümesinin bir elemanı ise, kendisinin de bir elemanıdır.

Russell bu çatışkının bir benzerinin Frege’nin mantık sisteminde ortaya çıktığını farkederek bunu Frege’ye yazdığı bir mektupla bildirmiştir.

Bu sonuç sadece Frege’nin meslek yaşamında değil, çağdaş mantığın bugüne kadarki gelişiminde de büyük önem taşımaktadır. Frege ve Russell’la başlayarak, Russell çatışkısına pek çok çözüm önerisi geliştirilmiştir.

Russell bağıntılar mantığının kullanışlı bir sistem olmasını engelleyen sınırlılıklarını aşarak genelleştirmeyi başarmıştır. Böylece Leibniz’den beri bir sorun olarak duran gündelik dildeki karmaşık önermelerin mantıksal çözümlemesinde önemli bir ilerleme elde edilmiştir.

Russell’ın çağdaş mantığın yaygın kullanımı açısından büyük önem taşıyan bir başarısı niceleme mantığının gösterimini (notasyonunu) daha kolay anlaşılır hâle getirmesidir.

Niceleme mantığının felsefedeki en iyi bilinen etkili uygulama denemelerinden biri, Russell’in belirli betimleme önermelerini çözümlemesidir.

Belirli betimlemeler “Türkiye’nin başkenti”, “En ünlü Türk romancısı” gibi belirli bir varlığa betimleme yoluyla işaret eden ifadelerdir. Genel olarak Russell’ın çözümlemesine göre, “F olan biricik şey G dir” önermesinin niceleme mantığının sembolik dilindeki karşılığı aşağıdaki gibidir:

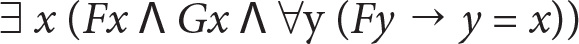
Gödel ve Matematiğin Sınırları

Kurt Gödel (28 Nisan 1906-14 Ocak 1978) o zaman Avusturya-Macaristan imparatorluğu sınırları içindeki Brünn şehrinde doğmuştur. Gödel, mantık çalışmalarında mantık ve matematik dünyası dışında da yaygın tanınmasını sağlayan pek çok önemli sonuca ulaşmıştır.

• Tamlık Teoremi: Hilbert ve Ackerman ilk kez 1928’de yayımlanan Grundzüge der Theoretischen Logik (Matematiksel Mantığın İlkeleri) içinde, birinci-basamak mantık için bir belit sistemi ortaya koymuştur.
• Eksiklik Teoremleri: Gödel’in adının mantık dünyasında ve başta felsefe olmak üzere, diğer alanlarda sıklıkla anılmasını sağlayan başarısı eksiklik teoremleridir. Eksiklik teoremleri Gödel’in Hilbert programı içindeki çalışmalarının bir sonucunda ortaya çıkmıştır. Hilbert programı matematiksel analizin tutarlılığını sadece sonlu kanıtlamalara başvurarak göstermeyi amaçlamaktaydı. Gödel matematiksel analizin temelini oluşturan aritmetiğin tutarlılık sorununun bile bu yolla çözülemeyeceğini göstermiştir.
• Birinci eksiklik teoremi: Aritmetiği içerecek yeterlilikte tutarlı bir biçimsel sistemde doğru aritmetik önermeleri belirten ancak bu sistemde kanıtlanamayan önermeler vardır.
• İkinci eksiklik teoremi: Aritmetiği içerecek yeterlilikte tutarlı hiçbir biçimsel sistemde, aritmetiğin tutarlı olduğunu belirten önerme kanıtlanamaz.
• Seçme Belitinin Bağımsızlığı: Seçme (veya seçim) beliti, boş-olmayan kümelerden oluşan her aile için (yani, her bir elemanı boş-olmayan bir küme olan her küme için) bu ailenin her kümesinden bir eleman seçen bir fonksiyonun varolduğunu söyleyen belittir. Bu belit, saf matematikçilerin neredeyse tümü tarafından doğru kabul edilirken, uygulamalı matematikçilerin çoğunu rahatsız eder. Saf matematikte elde edilen pek çok önemli sonuç seçme belitine veya görünüşte farklı bir önerme olan ama seçme belitine denk bir önermeye dayanmaktadır. Aşağıdaki ilkeler, seçim belitinin denklerinden en sık başvurulanlar arasındadır.
  • İyi-sıralama ilkesi: Her küme iyisıralanabilir. Yani, her S kümesi üzerinde, bu kümenin her boş-olmayan T altkümesinin bir R-minimum elemanı (yani, “her t ? T için t ₀ Rf ” şartını sağlayan bir t ₀ ? T elemanı) olacak şekilde bir R kısmi sıralama bağıntısı vardır.
  • Zorn lemmasi: S bir küme, R ise S üzerinde bir kısmi sıralama bağıntısı (yansımalı, antisimetrik ve geçişli bir 2-li bağıntı) olsun.S içinde R bağıntısına göre her zincirin (her iki x, y elemanı için ya xRy ya da yRx şartını sağlayan alt-küme) bir üst sınırı (zincirin tüm elemanlarından büyük bir s e S elemanı) varsa, S kümesinin bir R-maksimal elemanı vardır (Birden çok maksimal eleman olabilir). Seçme belitinin, genellikle “Banach-Tarski paradoksu” olarak adlandırılan, aşağıdaki sonucu fizik evren hakkındaki sağduyuya aykırı görülmektedir.
  • Banach-Tarski Teoremi: S = {(x,y,z) ? R ³ : x ² + y ² + z ² < 1} noktalar kümesi ile belirlenen 3-boyutlu birim küreyi sonlu sayıda parçaya bölelim. Bu parçalardan, sadece döndürme ve taşıma ve yenidenbirleştirme ile (bu işlemler sırasında bir parçanın diğeri içinden geçmesine izin vererek) S küresinin iki kopyası elde edilebilir.

Çeşitli Mantık Sistemlerinin Gelişmesi

İlk olarak Frege’nin tam bir sistemini sunmayı başardığı birinci basamak niceleme mantığı özellikle matematikteki uslamlamada yaygın mantık sistemi olarak benimsenmiştir. Bununla birlikte kimi mantıkçılar bu mantık sistemini yetersiz bulmuş veya yaygın mantığın kimi yönlerini olumsuz görerek, farklı mantık sistemleri geliştirmiştir. Bunlar arasında öne çıkanlardan bazıları çoklu-değerli (ing. many-valued) mantık sistemleri, sezgici mantık sistemleri ve kipli mantık sistemleridir.

Çoklu-değerli mantıklar, sezgici mantıklar ve diğer bazı mantık sistemlerinin özellikleri mantık felsefesinde önemli bir tartışma konusunu oluşturmakla birlikte, bu sistemler felsefede yaygın kullanılmamaktadır. Kipli mantık sistemlerine ise (özellikle çağdaş çözümlemeli felsefede) bu diğer mantık sistemlerine oranla daha yaygın başvurulmaktadır. Bu nedenle, çağdaş mantığın gelişiminin sadece ana hatlarını verme olanağı bulunan giriş niteliğindeki bu ünitede sadece kısaca kipli mantığın gelişimine yer verebileceğiz.

Kipli mantık sistemlerinin doğmasının ardında gündelik dilde “ise” koşul ekleminin yaygın mantıkta kimi zaman “zayıf gerektirme” diye adlandırılan yorumuna yönelik eleştiriler yatmaktadır. Örneğin, koşul ekleminin tanımı gereği:

1. Ön-bileşen (A) yanlış bir önerme olduğunda, artbileşen (B) hangi önerme olursa olsun, A ^ B koşul önermesi doğrudur.
2. Art-bileşen (B) doğru bir önerme olduğunda, önbileşen (A) hangi önerme olursa olsun, A ^ B koşul önermesi doğrudur.

Lewis kipli mantık sistemleri üzerine o zamana kadar yaptığı ve farklı tarihlerde yayımladığı çalışmalarının sonuçlarını Bir Sembolik Mantık Araştırması (1918) sisteminde toplamıştır. Emil Post buradaki kipli mantık sisteminde olanaksızlık ile yanlışlığın denk olduğunu ortaya koymuştur. Bu durumda mantık yazınında, içlem mantığı olması gereken kipli mantığın kaplamlı önermeler mantığına “çökmesi” denilen durum gerçekleşmiş olmaktadır. Bunun üzerine Lewis, 1918’deki kipli mantık sisteminde yer alan bir beliti değiştirmek zorunda kalmıştır (Lewis, 1920).

Çağdaş mantıkçılar arasında kipli mantık için kullanışlı ve sağduyusal bir yorum (semantik) geliştirmeyi ilk başaran Rudolf Carnap’tır (1891-1970). Carnap’ın kipli semantiğinde başvurduğu temel kavram “durum betimlemesi” kavramıdır. Durum betimlemesi kavramı Carnap’a göre Leibniz’in “olanaklı dünyalar” ya da Wittgenstein’m “olanaklı olgu durumları” kavramlarıdır (Carnap, 1947. s. 9-10).

Çağdaş mantıkta kipli önermelerin yorumlanması konusunda en önemli adım Saul Kripke’nin olanaklı dünya semantiğini geliştirmesidir (Kripke, 1959). Kripke semantiği ile kiplerin kolayca kavranan bir formel yorumlamaya kavuşmaları kipli mantık sistemlerine özellikle çözümlemeli felsefe ve kuramsal bilgisayar bilimi alanlarında yaygın olarak başvurulmasını sağlamıştır.