MATEMATİKSEL İKTİSAT - Ünite 6: Çok Değişkenli Fonksiyonlar Özeti :
PAYLAŞ:Ünite 6: Çok Değişkenli Fonksiyonlar
Çok Değişkenli Fonksiyon Kavramı
Çok değişkenli fonksiyonların temel özelliklerini gözden geçirip bu tür fonksiyonların iktisatta kullanımı ile ilgili örnekler vereceğiz. Çok değişkenli fonksiyonların en basit biçimi iki değişkenli fonksiyonlardır.
İki Değişkenli Fonksiyonlar
Boş küme olmayan A, B ve C kümeleri verilsin.
A×B ={(x, y) : x ? A, y ? B}
A×B kümesinden alınmış her (x, y) çifti C kümesinde tek bir z elemanına eşleyen bir
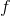 bağıntısına iki değişkenli fonksiyon denir.
bağıntısına iki değişkenli fonksiyon denir.
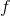 : A×B ›
: A×B ›
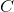 ,
,
 =
=
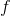 (
(
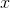 ,
,
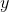 )
)
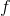 =
=
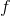 (
(
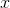 ,
,
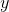 )
)
şeklinde gösterilir. İki boyutlu düzlem
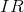 2
ile gösterilir.
2
ile gösterilir.
İki Değişkenli Fonksiyonun Tanım Kümesi
İki değişkenli fonksiyonun tanım kümesine, düzlemin bir alt kümesi olduğu için tanım bölgesi denir. İktisadi analizlerle bizim en sık karşılaştığımız tanım bölgesi
{(x, y) : x ? 0,
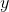 ? 0,
? 0,
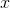 ,
,
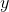 , ?
, ?
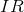 }
}
kümesidir.
İki Değişkenli Fonksiyonun Grafiği
İki değişkenli bir fonksiyonun grafiği tüm (
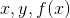 ,) noktalarını içeren üç boyutlu uzayda bir yüzeydir. Fonksiyonun bağımlı değişkenlerinden oluşan ikili (x, y )’ yi yatay düzlemde gösterirsek fonksiyonun değeri bu noktanın üzerinde yer alan ve yüksekliği
,) noktalarını içeren üç boyutlu uzayda bir yüzeydir. Fonksiyonun bağımlı değişkenlerinden oluşan ikili (x, y )’ yi yatay düzlemde gösterirsek fonksiyonun değeri bu noktanın üzerinde yer alan ve yüksekliği
 ile belirlenen yüzeydir.
ile belirlenen yüzeydir.
İkiden Fazla Değişkenli Fonksiyonlar
İktisatta incelediğimiz fonksiyonların çoğu ikiden fazla bağımsız değişken içerir.
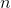 ? N olmak üzere, boş küme olmayan
A1, A2, ..., An
ve C kümeleri verilsin.
? N olmak üzere, boş küme olmayan
A1, A2, ..., An
ve C kümeleri verilsin.
x1 ?A1, x2? A2, …, xn ?An olmak üzere, tüm (x1, x2, ..., xn) sıralı
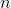 -lilerin kümesine A1, A2, ..., An kümelerinin kartezyen çarpımı denir ve
-lilerin kümesine A1, A2, ..., An kümelerinin kartezyen çarpımı denir ve
A1×A2×...×An şeklinde gösterilir.
Kısaca A1×A2×...×An = { (x1, x2, ..., xn):x1? A1, x2? A2, ..., xn ?An} olur.
Her bir (x1, x2, ..., xn) ?A1×A2×...×An
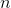 -lisine
-lisine
C kümesinden bir tek z elemanı atayan ƒ kuralına
A1×A2×...×An’ den C ’ye n-değişkenli fonksiyon denir ve
ƒ : A1×A2×...×An ›C, z = ƒ (x1, x2, ..., xn) veya ƒ (x1, x2, ..., xn) şeklinde gösterilir.
A1×A2×…×An kümesine fonksiyonun tanım kümesi veya tanım bölgesi, C ’ye ise değer kümesi denir.
Kısmi Türev
f(x, y) fonksiyonu, üretim sürecinde x ve y gibi iki farklı girdi kullanan bir firmanın kâr fonksiyonu ise, her iki girdideki değişim sonucunda kârın nasıl etkileneceğini bilmek firma açısından önemlidir.
z = ƒ(x, y) iki değişkenli fonksiyonunda, ƒ ’nin x’e göre kısmi türevi
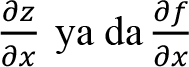 ya da ƒx şeklinde gösterilir.
ya da ƒx şeklinde gösterilir.
Benzer olarak, ƒ ’nin y’ye göre kısmi türevi
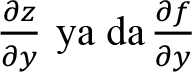 ya da ƒy şeklinde gösterilir.
ya da ƒy şeklinde gösterilir.
Çok değişkenli fonksiyonun genel gösterimi
y = ƒ (x1, x2,.....,xn) şeklindedir. Buradan
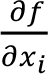
ya da ƒ
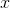 i
(i = 1,2,......,n) ile gösterilen n tane kısmi türev bulunabilir. Bunu yaparken her seferinde fonksiyonun bir değişkene göre türevini alıp kalan
i
(i = 1,2,......,n) ile gösterilen n tane kısmi türev bulunabilir. Bunu yaparken her seferinde fonksiyonun bir değişkene göre türevini alıp kalan
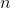 – 1 değişkenin sabit olduğunu kabul ederiz.
– 1 değişkenin sabit olduğunu kabul ederiz.
İkinci Dereceden Kısmi Türevler
z = ƒ(x, y ) ise z ’nin x ve y ’nin bir fonksiyonu olduğunu biliyoruz. Aynı zamanda ƒx ve ƒy de x ile y ’nin birer fonksiyonudur.
Fonksiyonun x’e göre iki kez kısmi türevi alınırsa
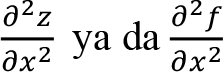 ya da
ya da
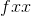
Fonksiyonun y ’ye göre iki kez kısmi türevi alınırsa
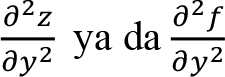 ya da
ya da
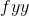
Fonksiyonun önce x’e sonra y ’ye göre kısmi türevi alınırsa
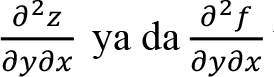 ya da ƒyx
ya da ƒyx
Fonksiyonun önce y ’ye sonra x’e göre kısmi türevi alınırsa
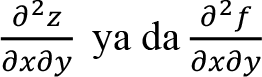 ya da ƒxy
ya da ƒxy
Kısmi türev, herhangi bir değişkendeki değişimin, diğer bütün değişkenler sabit tutulduğunda etkisini göz önüne alır. Bu iktisatta bize çok tanıdık olan bir kavramla aynı anlama gelmektedir. “Ceteris Paribus” yani diğer şeylerin sabit kaldığı varsayımı. İktisatta birçok analiz sadece bir değişken üzerinde yoğunlaşarak diğer faktörlerin sabit olduğu varsayımına göre yapılmaktadır.
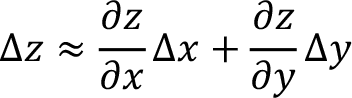
Bu ifade z’deki değişimi yaklaşık olarak hesaplasa da, ?
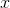 ve ?
ve ?
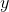 sıfıra yaklaştıkça hata payı azalacağı için formül bir eşitliğe dönüşür.
sıfıra yaklaştıkça hata payı azalacağı için formül bir eşitliğe dönüşür.
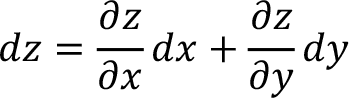
Burada dx, dy ve dz diferansiyellerdir ve ?x, ?y ve ?z ’nin limit değerlerini temsil ederler.
Çok Değişkenli Fonksiyonların İktisadi Uygulamaları
Esneklikler
Tek değişkenli fonksiyonları anlatırken talebin fiyatın bir fonksiyonu olduğunu ifade edip fiyatın artması durumunda talep edilen miktarın azalacağını söylemiştik. Çok değişkenli fonksiyonları kullanarak bu basitleştirilmiş ifadeyi geliştirerek talebi etkileyen diğer faktörleri de inceleyebiliriz. Bir malın talebinin (Q), malın fiyatına (P), ikame veya tamamlayıcı malın fiyatına (Pi ) ve tüketicinin gelirine (Y) bağlı olduğunu varsayalım. Bunu çok değişkenli bir fonksiyon kullanarak
Q = ƒ(P, P
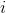 , Y)
, Y)
şeklinde gösterebiliriz.
Bu çok değişkenli fonksiyonda talebin fiyat esnekliği, ikame malının fiyatı ve tüketici geliri sabitken, malın kendi fiyatındaki yüzde değişim sonucunda, talepteki yüzde değişimi ifade etmektedir.
Talebin gelir esnekliği pozitif ya da negatif değer alabilir. Normal mallar için gelir arttığında talep de artacağından gelir esnekliği pozitif çıkar. Düşük mallarda ise gelir artışı sonucunda talep azalacağından gelir esnekliği negatiftir.
Fayda Fonksiyonu
Fayda fonksiyonu, tüketilen mal miktarlarının bir fonksiyonu olarak tüketiciye sağlanan tatmindir. İktisatta U ile gösterilen fayda fonksiyonlarıdır. Bir tüketicinin fayda fonksiyonu, toplam fayda veya tüketilen mal miktarlarının bir fonksiyonu olarak tüketiciler tarafından sağlanan tatmin olarak açıklanabilir. Tüketici M1 malından x1 birim ve M2 malından x2 birim tüketerek fayda sağlıyorsa fayda fonksiyonu
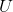 =
=
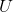 (
(
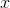 1,
1,
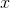 2)
2)
şeklinde gösterilebilir.
Fayda fonksiyonlarının grafik gösterimi farksızlık eğrileri ile olur. U = ƒ (x1, x2) fonksiyonu için oluşturulacak farksızlık eğrisi tüketicinin aynı fayda düzeyinde kalması koşulu ile x1 ve x2 mallarından tüketebileceği farklı miktarları göstermektedir.
Üretim Fonksiyonu
Üretim fonksiyonunda çıktı (Q), sermaye (K) ve emek (L) girdilerinin fonksiyonu olarak açıklanır:
Q = ƒ (K, L)
Sermayenin marjinal ürünü (MPK) emek girdisi sabitken, sermaye girdisindeki bir birim artışın çıktıda ortaya çıkaracağı artış olarak tanımlanır ve üretim fonksiyonunun sermayeye göre kısmi türevi alınarak bulunur.
Üretim fonksiyonunun grafiği eş ürün eğrileri ile gösterilebilir. Eş ürün eğrisi aynı çıktı düzeyini sağlayan emek ve sermaye girdilerinin farklı bileşimleridir. Eş ürün eğrisinin eğimine Marjinal Teknik İkame Oranı (MRTS) adı verilir. Eş ürün eğrisi üzerindeki herhangi bir noktada (
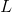 =
=
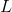 0
,
0
,
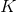 =
=
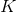 0
) eğimin değeri, emekteki bir birimlik artış sonucunda, sermayenin ne kadar azalacağının ölçüsüdür.
0
) eğimin değeri, emekteki bir birimlik artış sonucunda, sermayenin ne kadar azalacağının ölçüsüdür.
Üretim Fonksiyonunun Homojenliği ve Ölçeğe Göre Getiri
Q = f(K, L) biçimindeki bir üretim fonksiyonunda, herhangi bir n sayısı için
ƒ (
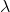 K,
K,
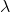 L) =
L) =
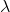 n
ƒ(K, L) ise
n
ƒ(K, L) ise
fonksiyonun homojen olduğu söylenir.
n = 1 ise fonksiyon ölçeğe göre sabit getiri sergiler. Yani girdilerdeki artış oranı ile çıktıdaki artış oranı aynıdır.
n < 1 ise fonksiyon ölçeğe göre azalan getiri sergiler. Yani girdiler belli bir oranda arttırıldığında, çıktıdaki artış bundan daha az olur.
n > 1 olduğunda fonksiyon ölçeğe göre artan getiri sergiler. Yani girdiler belli bir oranda arttırıldığında, çıktıdaki artış, bundan daha fazla olur.
Üretim fonksiyonlarının iktisatta çok sık kullanılan özel bir türü Cobb-Douglas üretim fonksiyonudur ve
Q = AK
 L
L
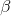
şeklinde gösterilir. Cobb-Douglas üretim fonksiyonunda;
 +
+
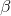 < 1 ise ölçeğe göre azalan getiri
< 1 ise ölçeğe göre azalan getiri
 +
+
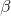 = 1 ise ölçeğe göre sabit getiri
= 1 ise ölçeğe göre sabit getiri
 +
+
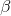 > 1 ise ölçeğe göre artan getiri
> 1 ise ölçeğe göre artan getiri
elde edilir.
Euler Teoremi
Homojen fonksiyonların sonuçları ile ilgili geliştirilen önemli fonksiyonlardan biri de Euler teoremidir. Buna göre ;
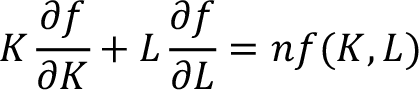
olarak elde edilir.
Azalan Marjinal Ürün
Bir üreticinin hangi koşullarda üretimini sürdürdüğünü kısmi türevleri kullanarak özetleyebiliriz. Normal olarak bir üretici, girdi miktarı arttığında çıktının da artmasını ister. Bunun için emeğin ve sermayenin marjinal ürününün pozitif olması gerekir.
Emek girdisi için
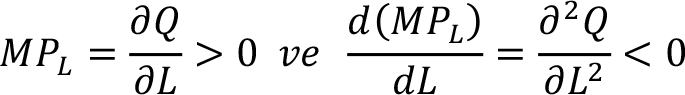
Sermaye girdisi için
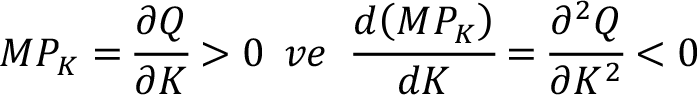
eşitlikleri ile bulunur.
Kâr Fonksiyonu
Firmanın üretim fonksiyonu ile ilişkili olan bir başka konu da kâr fonksiyonudur.
Çünkü çoğu ticari işletmenin nihai amacı kârını maksimize etmektir.
Eğer üretilen ürünün fiyatı P, sermayenin fiyatı olan faiz r ve emeğin fiyatı olan ücret oranı w ile gösterilirse, K birim sermaye ve L birim emek kullanan firmanın kâr fonksiyonu
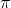 ( K, L) = TR - TC
( K, L) = TR - TC
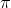 ( K, L) = PQ -
( K, L) = PQ -

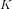 -
-
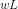
= PK
 L
L
 -
-
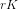 -
-
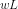
olur.


