Ünite 3: Üstel ve Logaritmik Fonksiyonlar

Üstel Ve Logaritmik Fonksiyonlara Giriş

Üstel fonksiyonlar ve bunların tersi olarak logaritmik fonksiyonlar ve bu tip fonksiyonların iktisat lisans eğitiminde nerede ve nasıl kullanıldığı bu ünitenin konularıdır. Örneğin sabit büyüme oranlı her türlü büyüme işlemi üstel fonksiyonlar ile tanımlanabilir. Nüfus artışı, yatırımlarda meydana gelen artış ve ya bir ülkenin GSYH’sinde meydana gelen büyüme, üstel fonksiyon temelli açıklanabilir. Yalnızca bu basit örnekler bile bir iktisat öğrencisi üstel ve logaritmik fonksiyonları neden tanımalı ve anlamalı sorularının yanıtını oluşturabilir.

Öncelikle, basitçe şu ayrımı yapmalıyız. Kuvvet fonksiyonları ve üstel fonksiyonlar birbirinden farklı iki tip fonksiyondur. şekil olarak benzerlik göstermeleri başlangıçta iktisat öğrencileri için şaşırtıcı olabilmektedir.

f(x) = y = x ^k genel şekliyle verilen basit kuvvet (güç) fonksiyonlarında, x taban ve k kuvvet (derece) olarak okunur. Tabanın pozitif ve üstün rasyonel sayı olması iktisat işlemleri için işlerimizi kolaylaştıracaktır. Burada x bir değişken iken, k bir sabittir. Bu durum üstel fonksiyonlarda değişecektir.

y = f(x) = x ²

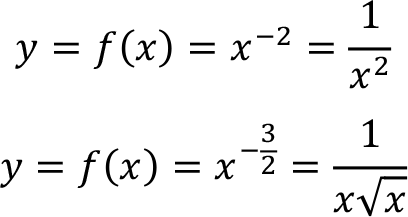
Yukarıdaki dört örnekte rahatlıkla izlenebileceği gibi, y bağımlı değişkeni bir tek x bağımsız değişkeni ile açıklanmaktadır. x’in üstünde yer alan sayılar ise yukarıda açıkladığımız k sabitini oluşturmaktadır.

Üstel fonksiyonlara baktığımızda ise değişkenin tabanda değil üstte yer aldığı izlenir. Tek değişkenli üstel fonksiyonlarda bağımsız değişken tabanda değil üstte yer alacaktır.

Bileşik Faiz ve e (Doğal Sayı) Sayısı

Varsayalım ki P0 > 0 (anapara) kadar paranızı vadeli mevduat hesabına yatırdınız ve bu hesap size r kadar sabit nominal yıllık faiz oranı önermektedir. Faiz ödemeleri yıl içerisinde düzenli aralıklarla n defa yapılmaktadır. Bir yıl sonunda anaparanın yeni durumunu gösteren hesap şöyle olacaktır:

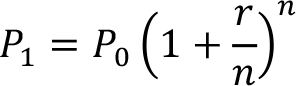
Peki, bankada paranızı bir yıl yerine t yıl tutuğunuzu varsayalım. Bu durumda hesabınızda olması gerekli P _t miktarında parayı gösteren bileşik faiz formülü şöyledir:

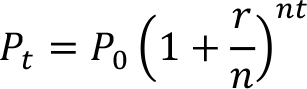
Yukarıdaki formüllerde yıl içerisinde her dönem ödenen faiz oranını ve nt faiz ödemelerinin t yılda toplam kaç kez yapılacağını gösterir.

Burada önemli bir noktayı belirtmeden geçmeyelim. Yukarıda t yılda belirli aralıklarla anaparanın nasıl büyüyeceğine dair genel formül görmekteyiz. Bu formül yalnızca bankalara yatırılan paranın gelecekte alacağı değeri hesaplamakta kullanılmaz. İktisatta büyüme hesabı yapılan bütün alanlarda bu formülü ya da bu formülün değişik versiyonları kullanılmaktadır.

Bu defa faizin her an uygulandığını varsayalım. Bir başka ifadeyle faiz devamlı bir şekilde anaparaya işlemektedir. Bu hesabı yapabilmek için geliştirilecek formülde e sayısı yani doğal sayı kullanılacaktır.

e sayısı şöyle tanımlanır:

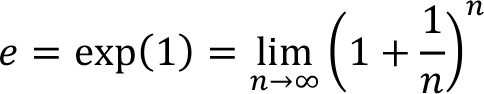
Artık t yıl sonra anaparanın sürekli işleyen bir faiz hesabıyla ne hâle geleceğinin formülünü yazabiliriz:

Pt = P ₀ e ^rt

Logaritmik Fonksiyon

Doğal logaritmik fonksiyon en temel şekliyle x = ln(y) şeklinde gösterilebilir ve y = e ^x doğal tabanlı üstel fonksiyonunun tersidir. Bir başka ifadeyle:

x = ln (y) ? y = ex ifadesi doğrudur.

Doğal logaritmik fonksiyonun grafiği basit olarak doğal tabanlı üstel fonksiyon grafiğinin x = y’ de çizilecek 45 derecelik doğruya göre aynadaki yansıması gibidir:

İktisat Uygulamaları

Üstel ve logaritmik fonksiyonlarla ilgili temel bilgilerden sonra şimdi de iktisat lisans eğitiminde kullanıldıkları bazı alanlardaki örnek uygulamaları kitabımızdan mutlaka inceleyelim.

Üstel Azalma

Deneysel tecrübelerle elde edilen bir bilgiye göre radyoaktif partiküllerin birçoğu üstel fonksiyon kaideleriyle azalma veya silinme seyri izlerler. Radyoaktif partikülün başlangıçtaki büyüklüğü Q0 olarak kabul edildiğinde zaman içerisinde azalmasını gösteren fonksiyon şöyle olacaktır:

Q (t) = Q _0e -kt

Yukarıdaki fonksiyonda k pozitif bir sabittir ve azalma oranını ifade eder. Bu oran genellikle başlangıç miktarının tam yarısına kadar azalma olabilmesi için gerekli olan zamana göre tanımlanır. Bu gerekli zaman da radyoaktif partikülün yarı-yaşamı (half-life) olarak adlandırılır.

Esneklik

Eğer talebin fiyat esnekliği 0 ve -1 aralığında ise o mal esnek olmayan mal olarak; yok eğer fiyat esnekliği -1 ile -? aralığında ise o mal esnek mal olarak ve son olarak da eğer fiyat esnekliği -1’e eşitse o mal da birim esnek mal olarak adlandırılır.

Fiyat Esnekliği

Aşağıdaki talep fonksiyonunu ele alalım:

Q ^d = 1000 - P ³ .

Bu fonksiyonda miktar ton cinsinden ve de fiyatlar t cinsinden olsun. Gerekli işlemlerden sonra ; P ³ <250 eşitsizliği elde edilir. Son olarak eğer fiyat (P) yaklaşık olarak 6,3’ten küçük olursa esnek olmayan talepten bahsedebiliriz. P ³ =250 olduğu zaman talep fiyata göre birim esnek ve bu değerden büyük ise talep esnektir.

Toplam Hasıla

Aşağıdaki talep fonksiyonunu ele alalım:

Q ^d = 1000 - P ³ .

Gerekli işlemlerden sonra;

Bu durum P ³ = 250 düzeyinin solunda toplam hasılanın artmakta olduğunu, sağında ise azalmakta olduğunu ifade eder.

Ters Talep

Aşağıdaki talep fonksiyonunu ele alalım: Q ^d = 1000 - P ³ .

Gerekli işlemlerden sonra;

(P ^d ) ³ =1000 -Q denklemini elde ederiz ki bu son denklem iktisatta ters talep fonksiyonu olarak adlandırılır.

Marjinal Hasıla

Aşağıdaki talep fonksiyonunu ele alalım:

Q ^d = 1000 - P ³ .

Gerekli işlemlerden sonra;

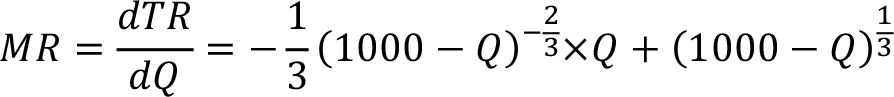
Denklemi bizim marjinal hasıla denklemimizdir.

Esneklik ve Logaritma

Varsayalım ki, Q ^d (P) şeklinde tanımlı bir talep fonksiyonu için elimizde fiyat ve miktar (P, Q) noktalarını gösteren veri kümesi bulunmaktadır. Yine varsayalım ki çok dar bir fiyat kümesi için doğrusal tahminleme modeli çalıştırdık. Ama bu tahminlemeyi elimizdeki orijinal veriler için değil değişime uğrayıp (x, y) = (ln P, lnQ) halini almış veriler için yaptık. Doğrusal tahminleme model sonuçlarımızın bize verdiği eğim, talep fonksiyonunun değil de logaritmik transformasyona uğramış talep eğrisinin eğimini yaklaşık olarak verir. Yani burada tahmin edilmiş olur. Zincir kuralını iki kere uyguladığımızda

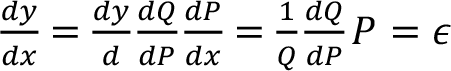eşitliği elde edilir. Bir başka deyişle, logaritmik transformasyona uğrayarak doğrusal hale gelen talep fonksiyonlarında lnQ’nın lnP’e göre türevi hesaplanırsa bu bize esnekliği verecektir.

Diğer Esneklikler

Talebi belirleyen faktörler incelenirken, yalnızca ilgili malın fiyatı değil, gelir, zevk ve tercihler, diğer malların fiyatları gibi etkenlerinde konunun ilgisini oluşturduklarını biliyoruz. Ancak basit talep ve arz denklemleri yardımıyla piyasada neler olduğunu anlayabilmek için ilgili malın fiyatı hariç diğer değişkenler analiz boyunca sabit kabul edilmişti. Talebi etkileyen diğer faktörlerden gelir ve diğer malların fiyatları serbest bırakıldığında bir mal için talep fonksiyonu,

Q ^d = 100 - p + 2p* - 3y gibi yazılabilir. Bu fonksiyonda p ilgili malın fiyatını, p* başka bir malın fiyatını ve y geliri temsil etmektedir. Denklemi buradaki gibi üç ayrı açıklayıcı değişkenle yazdığımız da artık kısmi türev kurallarını kullanarak çeşitli esneklik hesaplamalarını yapabiliriz.