Ünite 7: Kısıtsız Optimizasyon

Optimizasyon

Kıt kaynaklarla sınırsız ihtiyaçların karşılanması probleminin çözümüyle ilgilenen iktisatçılar temelde ekonomik birimlerini seçim yapma süreçlerini inceler. Bu seçim elbette mevcut koşullar altında en iyisinin seçimi amaçlandığı için optimizasyon olarak adlandırılır. Yani bu bağlamda ekonomik birimlerin rasyonel davranarak, diğer koşullar sabitken kendisi için en iyisini yapmaya çalışmasına optimizasyon denir.

Optimizasyonu matematikçiler, bağımsız ve bağımlı değişken arasındaki ilişkiyi ifade eden fonksiyonun birinci türevini sıfır yapan nokta ya da noktalar optimal (maksimum ya da minimum) değerler olarak ifade edilir. Matematikçiler ise bu optimal noktayı bulma yöntemine optimizasyon adı verilir.

Her iktisadi model belirli bir amaç doğrultusunda ulaşılmak istenen sonuçların optimum yapılması veya denge durumlarıyla ilgilenir. Dolayısıyla “ Bir firmanın kârını maksimum yapabilmek veya maliyetini minimum yapabilmesi için üretim miktarı ne olmalıdır?” gibi amaçlar doğrultusunda optimal işlemler yapılır.

Tek Değişkenli Fonksiyonlarda Kısıtsız Optimizasyon

Tek değişkenli bir fonksiyon, x bağımsız değişkeni (seçim değişkeni ya da karar değişkeni) ve y bağımlı değişkeni (sonuç değişkeni) göstermek üzere y=f(x) şeklinde gösterilir. Burada ele alınan f(x) fonksiyonu sürekli ve en az iki defa türevlenebilir olmalıdır. Bu şekilde ifade edilen ve doğrusal olmayan fonksiyonun maksimumu ya da minimumu olup olmadığına karar verebilmek için gerek ve yeter koşul birinci türevini sıfır yapan kritik nokta ya da noktaların belirlenmesidir. Yani bir fonksiyonun birinci türevini sıfır yapan değer veya değerlere kritik nokta denir. Bu gerekli koşul sağlanınca ikinci türev alınarak maksimum ve minimum için koşul sağlanmış olur.

Yerel maksimum ve minimum noktasını bulma işlemi,

• Kritik noktalar bulunur.
• Kritik noktaların artan ve azalan olduğu aralıklar incelenir (S:160, Şekil 7.1). Kendisinden küçük değerler için azalan ve kendisinden büyük değerler için artan değer alan kritik noktaya yerel minimum; kendisinden küçük değerler için artan ve kendisinden büyük değerler için azalan değerler alan kritik nokta değerine yerel maksimum noktası denir.

Yerel maksimum ve minimum için ikinci türev yöntemi adımları,

• Kritik noktalar bulunur.
• Bulunan kritik noktalar ikinci türevde yerine konularak sıfırdan küçük değer alıyorsa maksimum yapan değer, sıfırdan büyük değer alıyorsa minimum yapan değerdir.

Tek değişkenli fonksiyonlarda optimal nokta bulma işlemi iktisadi uygulamalarda tüketim, tasarruf, fayda, milli gelir, toplam hasıla, toplam maliyet, talep, arz, para talebi, para arzı gibi çok sayıda iktisadi fonksiyonda kullanılmaktadır. Bu fonksiyonlarda optimizasyon yaklaşımı kullanımını görmek için kâr örneği ile adım adım açıklamaya çalışalım.

• Bir firmanın kâr fonksiyonunu optimal değerleri belirlenmeden önce firmanın amacı saptanmalıdır.
• Kâr fonksiyonu için firma amacı kârını maksimum yapmaktır. Tek ürün üretildiği bir şirketi düşünelim. Kâr=Toplam hasıla(TR)- Toplam maliyet(TC)

? (Q) = TR (Q) - TC (Q)

Burada Q üretim miktarını temsil eder.

• Firmanın kârını maksimum yapan üretim düzeyini bulabilmek için kâr fonksiyonunun birinci türevini sıfır yapan üretim fonksiyonu bulunmalıdır.

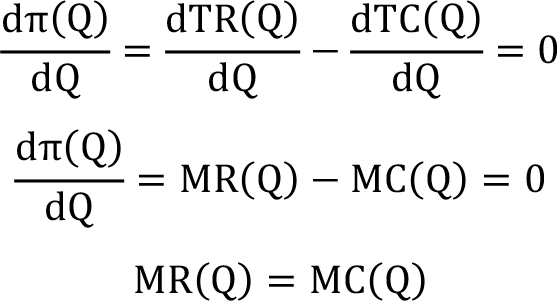
Sonucu bulunur. Yani marjinal hasıla(MR(Q)) marjinal maliyete(MC(Q)) eşit olmuş olur. Tüm piyasa koşullarında bu eşitliğin maksimizasyonu sağlanmalıdır. Tabii bu matematiksel bir eşitlik olup tam rekabet koşullarında MR(Q)=P olarak alınıp iktisadi mantık matematiksel olarak gösterilir.

• Firmanın üretim miktarını sıfır yapan üretim değer ya da değerlerinin maksimum olup olmadığına karar verebilmek için ikinci türevi alınıp birinci türevi sıfır yapan değerler ikinci türevde yerine konulur.

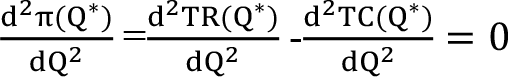
Eğer ikinci türev değeri negatif değer veriyor ise birinci türevde elde edilen kritik değer ya da değerler firmanın karını maksimum yaptığı, pozitif çıkarsa minimum yaptığı tabii firma karını maksimum yapacak değerde üretim yapmalıdır.

Çok Değişkenli Fonksiyonlarda Kısıtsız Optimizasyon

Ne kadar tek değişkenli fonksiyonlarla işlemleri basite indirgemeye çalışsak ta iktisadi problemlerde, fonksiyonlar genellikle çok değişkenli ve ekonomik birimlerin hedefleri çok sayıda değişkene bağlıdır. Bir  firmanın üretim fonksiyonu, üretim sürecinde kullanmış olduğu emek, sermaye ve hammadde miktarı gibi birden fazla faktöre bağlıdır. Buna göre, n sayıda değişkene bağlı z fonksiyonu

z = f(x ₁ , x ₂ , … , x _n )

şeklinde gösterilir.

Tek değişkenli fonksiyonlarda optimal (yerel maksimum ve yerel minimum) noktalarının nasıl bulunacağı gösterilmişti. Şimdi iki ve üç ürün üreten firmaların amaç fonksiyonuna bağlı olarak kar fonksiyonunun optimal değerlerini bulunması ele alınacaktır.

İki değişkenli fonksiyonlarda kısıtsız optimizasyon: İki değişkenli bir fonksiyon (x ₁ , x ₂ ) bağımsız değişkenleri ve z bağımlı değişkeni göstermek üzere

z = f(x ₁ , x ₂ )

şeklinde gösterilip, iki değişkenli fonksiyonunun yerel maksimum ya da yerel minimum değerlerinin bulunması için aşağıdaki adımlar izlenir.

1. z = f(x ₁ , x ₂ ) fonksiyonunun birinci mertebeden kısmi türevleri eş anlı olarak alınır ve sıfıra eşitlenir.
   
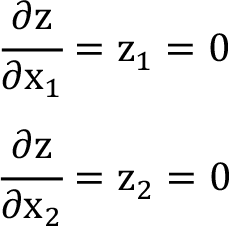
   Bu işlemler sonucunda birinci mertebeden kısmi türevini sıfır yapan sıralı ikililer bulunur.
2. Bu sıralı ikililer (a, b) ise, z = f(x ₁ , x ₂ ) ikinci mertebeden kısmi türevleri alınır ve bu sıralı ikililer kısmi türevlerde yerine konur;

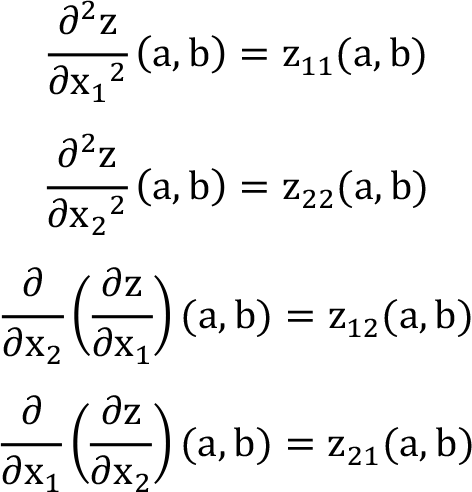
(a, b) sıralı ikilisinin yerel maksimum ya da minimum olup olmadığına karar verebilmek için gerekli koşul Hessian matrisinin determinant değerinin sıfırdan büyük olması gerekliliğidir. Daha sonra asal minörlerinin işaretlerinin işaretlerine bakılır. Hessian matrisinin detayı için (S: 164)’e bakınız. Hessian matrisi kısaca ikinci mertebeden kısmi türevlerden elde edilen matristir. Hessian matrisinin özellikleri ve önermelerden özetle,

• Eğer z ₁₁ (a, b) > 0 veya z ₂₂ (a, b) > 0 asal minörleri ise (a, b) sıralı ikilisinin yerel minimum olduğu söylenir.
• Eğer z ₁₁ (a, b) < 0 veya z ₂₂ (a, b) < 0 asal minörleri ise (a, b) sıralı ikilisinin yerel maksimum olduğu söylenir.
• Hessian matrisinin determinant değeri IHI < 0 ise ne maksimum ne de minimumu vardır. IHI = 0 ise bu sıralı ikililer için bir şey söylenmez.

Üç değişkenli fonksiyonlarda kısıtsız optimizasyon: üç değişkenli bir fonksiyon (x ₁ , x ₂ , x ₃ ) bağımsız değişkenleri ve z bağımlı değişkenini göstermek üzere z = f(x ₁ , x ₂ , x ₃ ) şeklindedir. Bu tip fonksiyonlarında yerel maksimum ya da yerel minimum değerlerin bulunması için aşağıdaki adımlar izlenir.

1. Birinci mertebeden kısmi türevler alınır ve eşanlı olarak sıfıra eşitlenir.
   
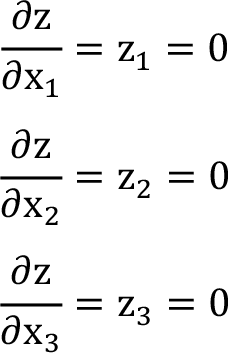
   Bu sıfıra eşitleme birinci mertebeden kısmi türevleri sıfır yapan değerler bulunur. Bu değerler (a, b, c) ise ikinci mertebeden kısmi türevlerine bakılır.
2. z = f(x ₁ , x ₂ , x ₃ fonksiyonunun ikinci mertebeden kısmi türevleri bulunur ve (a, b, c) değerlerinin yerel maksimum ya da minimum olup olmadığına karar verebilmek için Hessian matrisi oluşturulur ve asal minörlerinin işaretlerine bakılır. Z fonksiyonunun ikinci mertebeden kısmi türevleri,

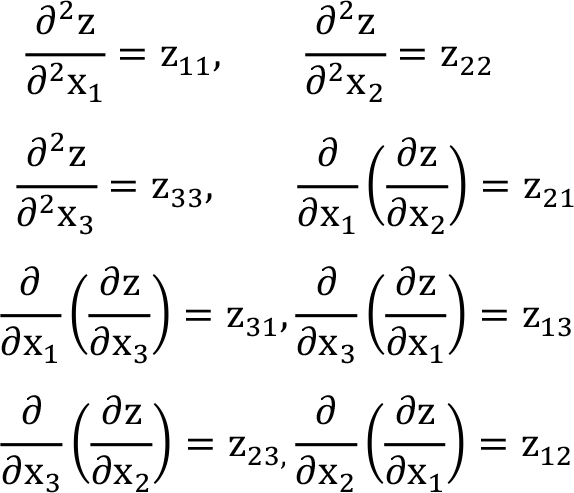
Oluşturulan Hessian matrisi,

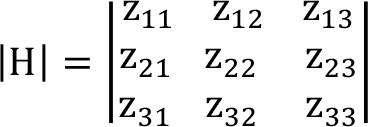
Şeklinde elde edilir.

Pozitif ve negatif belirlilik için, n. mertebeden simetrik bir matrisin bütün asal minörleri sıfırdan büyükse matris pozitif belirlidir. Eğer asal minörleri (-, +, -, +, …) şeklinde ise matris negatif belirlidir. Asal minörler,

• Hessian matrisi negatif belirli olduğunda (a, b, c) değerleri amaç fonksiyonunu maksimum kılan değerler olmuş olur.
  • Hessian matrisi pozitif belirli olduğunda (a, b, c) değerleri amaç fonksiyonunu minimum kılan değerler olmuş olur.

Asal minörlerle ilgili detaylı bilgi (S: 166) ve (S: 167)’den ulaşabilirsiniz.

Üç mal üreten bir firmanın amacına bağlı olarak kâr fonksiyonu düzenlenir ve iki değişkenli kar fonksiyonuna benzer şekilde

? Q ₁ , Q ₂ , Q ₃ =

TR (Q ₁ ) + TR (Q ₂ ) + TR (Q ₃ ) - TC(Q ₁ , Q ₂ , Q ₃ )

Biçiminde elde edilir ve yukarıda anlatılan adımlar takip edilerek fonksiyon optimize edilir.