Ünite 1: Türev ve Kuralları

Türev ve İktisadi Analiz

Türev kavramı, iktisadi analizleri matematik yardımıyla yapabilmemiz için önemli bir araçtır. İktisatta çok sık kullanılan analiz yöntemlerinden biri olan “karşılaştırmalı statik analiz”in gerçekleştirilebilmesi için türev kavramına ihtiyaç vardır.

Limit ve Süreklilik

İktisat alanında en fazla kullanılan matematiksel araçlardan biri olan türevin anlaşılabilmesi için, öncelikle limit ve süreklilik kavramlarını bilmemiz gerekir. Bir fonksiyonun türevinin mevcut olabilmesi için gerekli ilk koşul, sürekli olmasıdır. Süreklilik ise ancak limit kavramıyla belirlenebilecek bir özelliktir.

Limit Kavramı: Bir fonksiyonun bağımsız değişkeni belli bir değere yaklaşırken fonksiyonun yaklaştığı değerdir.

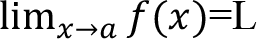
Bu ifade “ 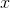, ’ya giderken fonksiyonun limiti L’dir” şeklinde okunur. Burada 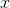’in ’ya yaklaştığını fakat asla değerini almadığını ve L’nin sonlu bir değer ifade ettiğini bilmeliyiz. L = ±? ise bu fonksiyonun limiti yoktur. Yani 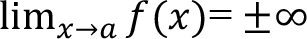ise bu fonksiyonun limiti yoktur.

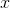
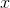
Sağdan Limit : ’ya ’dan büyük değerlerden yaklaşıyorsa “ ’ya sağdan yaklasıyor” deriz. Buna sağdan limit denir. Aşağıdaki gibi gösterilir:

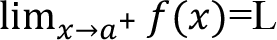
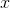
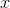
Soldan Limit : ’ya ’dan küçük değerlerden yaklaşıyorsa “ ’ya soldan yaklasıyor” deriz. Buna soldan limit denir. Aşağıdaki gibi gösterilir:

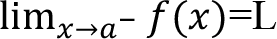
Eğer bir fonksiyonun sağdan ve solda limitleri mevcut ve birbirlerine eşit ise bu fonksiyonun limiti vardır.

Bir fonksiyonun a noktasında sağdan ve soldan limitleri mevcut olsa bile, bu limitler birbirine eşit değilse bu fonksiyonun noktasında limiti yoktur. Böyle bir fonksiyon (s:4, Şekil 1.1) gösterilmiştir. Şekilde x, ?’ya soldan yaklaşırken L ₁ ’e yaklaşmaktadır. x, ?’ya sağdan yaklaşırken fonksiyon L ₂ 'ye yaklaşmaktadır.

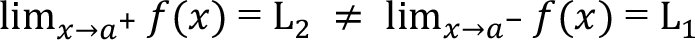
Bir Fonksiyonun Limitinin bulunması: y=f(x) fonksiyonunun x ?’ya yaklaşırken limitini bulmak için x’e, soldan ve sağdan ?’ya yaklaşan değerler vererek y’nin hangi değere yaklaştığına bakmamız gerekir. Limitin Özellikleri: Herhangi bir fonksiyonun limiti bulunurken limit ile ilgili bazı özellikler işimizi kolaylaştırır(s:5-6)

Süreklilik: Bir fonksiyonun limiti mevcut ise ve bu limit fonksiyonun değerine eşit ise o fonksiyon “sürekli” bir fonksiyondur. Buna göre f(x) fonksiyonu

1. ? noktasında tanımlı ise, yani f(a) mevcut ise
2. ? noktasında limiti var ise:
   
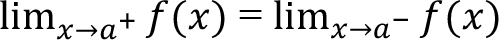
3. ve bu limit, fonksiyonun s noktasındaki değere eşit ise

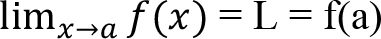
f(x) fonksiyonu ? noktasında süreklidir.

Sürekli fonksiyonların grafikleri de sürekli olur. Eğer bir fonksiyonun grafiğini çizdiğimizde, kesintiler veya sıçramalar görüyorsak bu fonksiyon sürekli değildir. (s:8, Şekil 1.2)’ de (b) panelindeki fonksiyon sürekli bir fonksiyon iken (a) ve (c) panellerindeki fonksiyonlar ise sürekli değildir.

Türev

Türev, birbiriyle ilişkili iki değişkenden biri artarken diğer değişkenin nasıl değişeceğini gösterir.

Değişim Oranı ve Türev: Değişim oranı, fonksiyonun değerindeki değişimin bağımsız değişkendeki değişime oranıdır.

Türev matematiksel olarak aşağıdaki gibi tanımlanır:

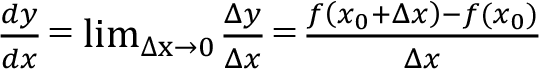
Aşağıdaki ifadelerin hepsi türevi ifade etmektedir:

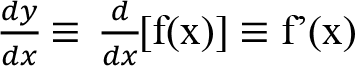
Bir y = f(x) fonksiyonunun x = x ₀ noktasındaki türevi, bu noktadan geçen teğetin eğimine eşittir.

Bir fonksiyonun türevi, yine bir fonksiyondur.

Türevi Alınabilir Fonksiyonlar: Bir fonksiyonun türevinin alınabilmesi için, iki koşulu sağlaması gerekir: (1) sürekli olması, (2) keskin köşelere sahip olmaması.

(s:10, Şekil 1.4)’ deki fonksiyon sürekli olmasına rağmen, x = 0 noktasında bir köşeye sahiptir. Bu nedenle fonksiyonun bu noktada türevi alınamaz.

Bir fonksiyonun türevinin alınabilmesi için, sürekli olması ve keskin köşelere sahip olmaması gerekir.

Türevin Anlamı: Bir fonksiyonun herhangi bir noktadaki türevi pozitif ise fonksiyon o noktada artandır. Bir fonksiyonun bir noktadaki türevi negatif ise fonksiyon bu noktada azalandır. Artan veya azalan fonksiyonlar, monoton fonksiyon olarak adlandırılır.

Bir fonksiyonun, artarken azalmaya döndüğü veya azalırken artmaya döndüğü noktalarda, fonksiyonun türevi sıfırdır yani yatay eksene paraleldir.

Türev Alma Kuralları

Sabit Fonksiyon Kuralı : k bir sabit ise, y = k gibi bir sabit fonksiyonun türevi sıfırdır: f’(x) = 0.

Kuvvet Fonksiyonu Kuralı : y = 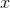^k gibi bir fonksiyonun türevi:

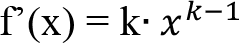
y= c. x ^k nın türevi: y = c•k•x ^k-1

Toplam Kuralı : f(x) ve g(x) gibi, türevi alınabilir iki fonksiyonun toplamlarının türevi, fonksiyonların ayrı ayrı toplamlarının türevine eşittir:

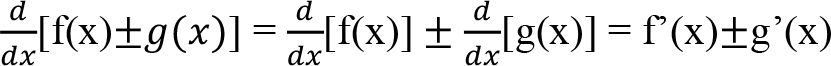
Çarpım Kuralı : İki fonksiyonun çarpımı olarak yazılabilen bir fonksiyonun türevini alırken aşağıdaki kural uygulanır:

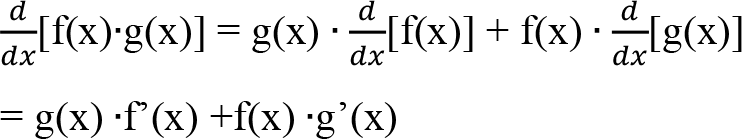
Bölüm Kuralı : f(x) ve g(x) gibi iki fonksiyonun böümünün türevi aşağıdaki gibi uygulanır:

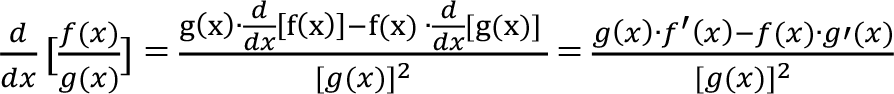
Zincir Kuralı: f(g(x)) gibi bir bileşke fonksiyonun türevi f’(x) = f’(g(x)) •g’(x) olarak elde edilir. Zincir kuralını aşağıdaki gibi ifade edebiliriz:

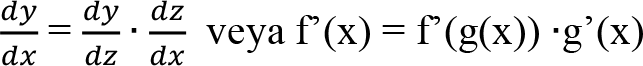
Üstel Fonksiyon Kuralı : y = e ^nx şeklindeki bir üstel fonksiyonun türevi alınırken aşağıdaki kural uygulanır:

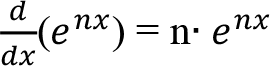
Bir g(x) fonksiyonu için;

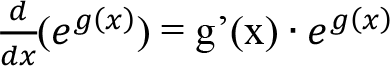
Logaritmik Fonksiyon Kuralı : y=ln x gibi bir fonksiyonun türevi aşağıdaki gibidir:

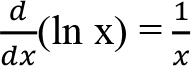
Logaritmik fonksiyon kuralı sıklıkla, bir değişkenin büyüme oranını bulmak için kullanılır. Bir y = f(x) fonksiyonunun “anlık büyüme oranı” aşağıdaki gibidir:

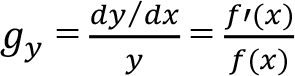
Büyüme oranı zaman ile ilgili bir kavram olduğu için, genellikle bağımsız değişken olarak x yerine, zamanı ifade eden t kullanılır. Fonksiyonun y = f(t) olarak yazarsak y’nin anlık büyüme oranı aşağıdaki gibidir:

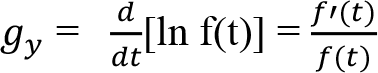
Ülke nüfusunu N ile gösterirsek nüfusun zaman içindeki artışını aşağıdaki gibi bir fonksiyon ile gösterilir:

N = N ₀ • e ^rt

Bu fonksiyonda N ₀ > 0 ve r > 0 birer sabit, t ise zaman değişkenini göstermektedir. Nüfus artış oranı:

g _{N = N ' / N}

N ' ₌ N ₀ • r . e ^rt

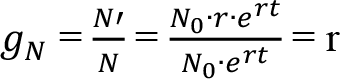
Bir ülkenin gayrisafi yurtiçi hasılasını Y(t) ile, nüfusu da N(t) ile gösterelim. Kişi başı yurtiçi hasıla, toplam gayrisafi yurtiçi hasıla, toplam gayrisafi yurtiçi hasılanın ülke nüfusuna ölünmesiyle elde edilir:

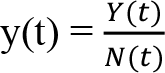
Kişi başına gayrisafi yurtiçi hasılanın büyüme oranı:

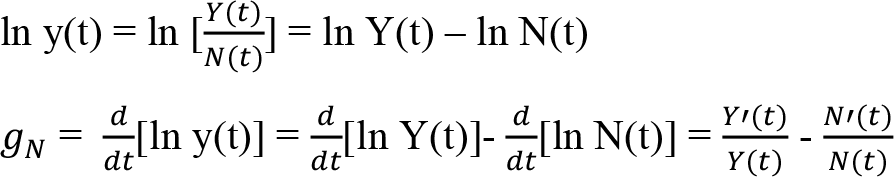
Trigonometrik Fonksiyon Kuralı: Temel trigonometrik fonksiyonların türevi aşağıdaki gibidir:

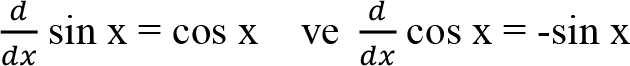
Kapalı Fonksiyon Kuralı : y = f(x) fonksiyonunu

F(y,x) ? y – f(x) = 0şeklinde kapalı bir fonksiyon olarak yazılır. Bu fonksiyonun türevi: F(y,x) = 0 ise,

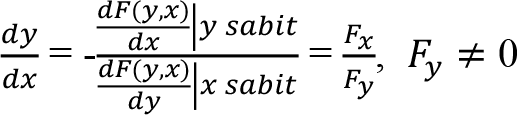
İkinci veya Daha Yüksek Dereceden Türevler

İkinci kez türev alınarak elde edilen fonksiyona “ikinci dereceden türev” veya kısaca “ikinci türev” adı verilir. y = f(x) gibi bir fonksiyonun ikinci türevi:

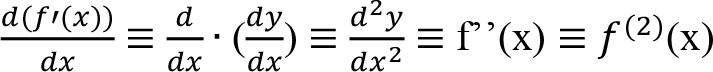
Fonksiyonun birinci türevi o fonksiyonun eğimi olduğuna göre,ikinci türev fonksiyonun eğiminin nasıl hareket ettiği hakkında bilgi verir. İkinci türev bir fonksiyonun eğiminin azaldığı, arttığı veya sabit kaldığı hakkında bilgi verir. İkinci türev pozitif ise eğim artmakta, negatif ise eğim azalmakta, sıfır ise eğim sabit kalmaktadır.

İkinci türevi daima pozitif olan fonksiyonlar, dışbükey fonksiyon olarak adlandırılır.

İkinci türevi daima negatif olan fonksiyonlar, içbükey fonksiyon olarak adlandırılır.

Üçüncü dereceden türevleri gösterirken :

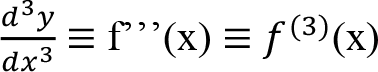
Marjinal Fonksiyonlar

Bir fonksiyonun türevi alınarak elde edilen fonksiyon “marjinal fonksiyon” olarak adlandırılır. Marjinal fonksiyon, bir fonksiyonun bağımsız değişkenindeki çok küçük bir değişimin fonksiyonun değerini nasıl değiştirdiğini gösterir. Dolayısıyla matematikteki türev kavramının iktisattaki karşılığıdır.

Marjinal Hasıla : Bir malın satışından elde edilen toplam hasıla (TR), malın fiyatı (P) ile satılan mal miktarının (Q) çarpımına eşittir.

TR = Q • P

Marjinal hasıla, toplam hasıla fonksiyonunun türevidir:

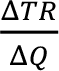
Monopolcü firma negatif eğimli bir talep fonksiyonu ile karşı karşıyadır. Firmanın sattığı ürün miktarı ile fiyatı arasında ters yönlü bir ilişki vardır.

Değişim oranı ile türev ifadelerinden elde edilecek marjinal hasıla değerleri birbirine çok yakın olacaktır:

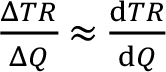Bunun nedeni, türevin çok küçük bir değişimi ifade etmesidir.

Ortalama hasıla, satılan birim başına hasıla değeridir ve toplam hasılanın satılan mal miktarına bölünmesiyle elde edilir:

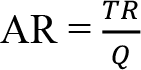
Toplam hasıla fonksiyonunu, ortalama hasılayı kullanarak ifade edebiliriz:

TR = P•Q =AR•Q

En sağdaki ifadenin türevini alırsak marjinal hasılayı, ortalama hasıla cinsinden ifade ederiz:

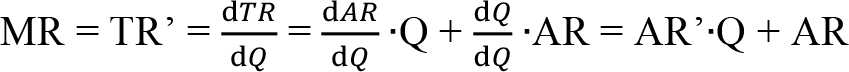
TR = a . Q - b. Q ² gibi bir toplam hasıla fonksiyonunda:

MR = a - 2•b•Q

AR = a-b•Q

Marjinal hasıla fonksiyonunun eğimi -2b iken, ortalama hasıla fonksiyonunun eğimi –b’dir. Yani marjinal hasıla fonksiyonu ortalama hasıla fonksiyonundan daha diktir(s:22, Şekil 1.6). Burada Q arttıkça toplam hasılanın önce arttığını sonra azaldığını görmekteyiz. Toplam hasıla Q = a/2b olana kadar artmaktadır. Bu nedenle Q < a/2b olan bölgede, yani Q = a/2b noktasının sol tarafında toplam hasılanın türevi pozitif olacaktır. Buna göre toplam hasıla artan fonksiyondur. Q > a/2b olan bölgede ise toplam hasıla azalan bir fonksiyondur. Diğer bir ifade ile, marjinal hasıla sıfırdan küçüktür.

Toplam fonksiyonun artan fonksiyondan azalan fonksiyona dönüştüğü, yani Q = a/2b olduğu noktada, türev sıfıra eşittir. (s:22, Şekil 1.6) da görüldüğü gibi, bu noktadaki teğet, miktar eksenine paraleldir, yani eğimi sıfırdır. Marjinal hasılanın sıfır olduğu bu nokta, aynı zamanda toplam hasılanın maksimum olduğu noktadır.

Tam rekabet firması miktar eksenine paralel bir talep fonksiyonu ile karşı karşıyadır. Ürün fiyatı satılan mal miktarından bağımsızdır ve firma piyasada oluşan fiyatı veri olarak alır.

Marjinal Maliyet : Marjinal maliyet, üretim miktarındaki bir birim artışın toplam maliyette meydana getirdiği artıştır. Marjinal hasılanın toplam hasıla fonksiyonunun türevi olduğu gibi, marjinal maliyet de toplam maliyet fonksiyonunun türevidir.

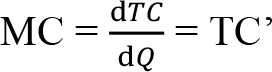
Toplam maliyet fonksiyonunun belli özelliklere sahip olması gerekir:

• i) Toplam maliyet fonksiyonu türevi önce azalan, sonra artan bir fonksiyon olmalıdır.
• ii) Üretim miktarı artarken toplam maliyet fonksiyonu asla azaltılmamalıdır.

(s:24, Şekil 1.7)’de görüldüğü gibi, toplam maliyet fonksiyonu monoton,yani sürekli artan bir fonksiyondur. Buna karşılık, marjinal ve ortalama maliyet fonksiyonları önce azalan, sonra artan bir grafiğe sahiptir. Bunun nedeni her iki fonksiyonun da karesel bir fonksiyon olmalarıdır.

Marjinal Ürün : Marjinal fiziki ürün, üretim fonksiyonunun türevi alınarak bulunur.

Firmanın üretim fonksiyonunun iki temel özelliğe sahip olması gerekmektedir: (1) istihdam edilen emek faktörü artarken üretim miktarı da artmalıdır, (2) üretim miktarındaki artış, azalan oranda olmalıdır. İlk özellik emeğin marjinal fiziki ürününün pozitif olması gerektiğini söylemektedir. Yani, üretim fonksiyonunun türevinin pozitif olması anlamına gelmektedir. İkinci özellik ise, azalan marjinal fiziki ürün veya azalan verimler yasasına karşılık gelmektedir. Yani, üretim fonksiyonunun ikinci türevinin negatif olması demektir. Üretim miktarı Q ile, emek faktörü L ile, emeğin marjinal fiziki ürününü ise MP _L ile gösterirsek, 1. ve 2. özellik aşağıdaki gibidir:

1. Özellik:
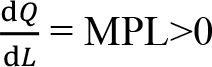
2. Özellik

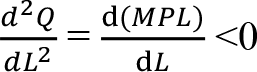
Üretimde kullanılan üretim faktörlerini sermaye ve emek olarak iki gruba ayırabiliriz. Bir faktörden daha fazla kullanıldığında, artırılan miktarı ile üretim miktarını sabit tutmak için diğer faktörlerden azaltılması gereken miktar arasındaki orana marjinal teknik ikame oranı denir ve MRTS ile gösterilir. Buna göre:

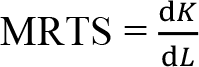
Esneklik

Talebin fiyat esnekliği, veya kısaca talep esnekliği, fiyattaki bir değişimin satılan mal miktarını nasıl etkileyeceğini gösteren ölçüttür. Talep esnekliği:

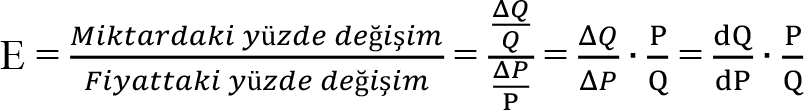
Esnekliğin mutlak değerinin birden küçük, birden büyük ve bire eşit olmasına göre talep hakkında aşağıdaki değerlendirmeler yapılır:

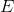• | |<1 ise “inelastik” talep.
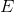• | |=1 ise “birim esnek” talep.
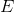• | |>1 ise “esnek” talep.

Talep edilen miktarı, fiyatın bir fonksiyonu olarak ifade eden fonksiyona ters talep fonksiyonu adı verilir.

Toplam hasıla TR = PQ olduğuna göre, fiyat artışının toplam hasıla üzerindeki etkisini görmek için:

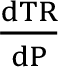türevini bulmalıyız.

TR(P) = P•Q(P)

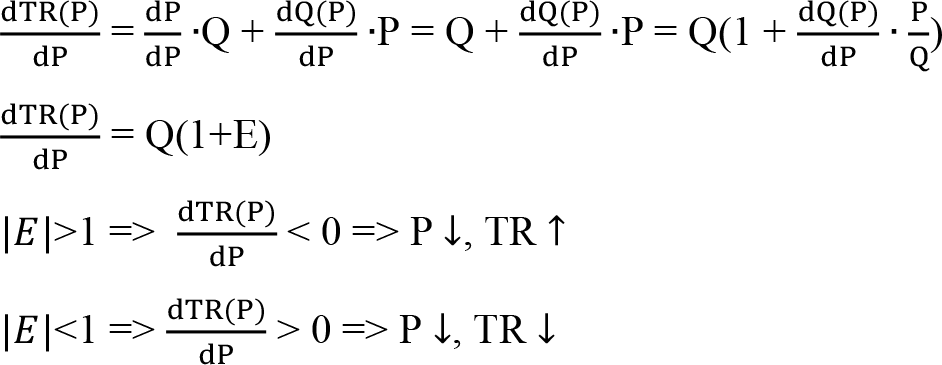
Eğer | 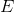|=1 ise, dRT/dP = 0 olacaktır ve fiyat değişikliği toplam hasılayı etkilemeyecektir.

Tüketim ve Tasarruf

Marjinal tüketim eğilimi, tüketim fonksiyonunun türevi alınarak bulunur. Keynesyen tüketim fonksiyonunun toplam tüketim harcamalarını (C), gelir (Y) ile açıklanır: C(Y).

Marjinal Tüketim Eğilimi (MPC) 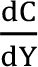= C' = c ₁

Toplam gelirin tüketime gitmeyen kısmı tasarruf edilmektedir.: Y = C+S.

Y = C+S => S = Y – C = Y – c ₀ – c ₁ Y = -c ₀ + (1-c ₁ )Y

Marjinal Tasarruf Eğilimi(MPS) = 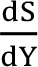= S' = 1 - c ₁

Marjinal tasarruf eğilimi, tasarruf fonksiyonunun türevi alınarak bulunur.