Chapter: 6 Derivative and its Applications

Derivatives of Functions

The derivative of a function f(x) is another function f'(x) , defined by

The derivative at some specific point x = a is a number defined by

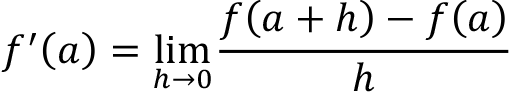
Equivalent symbols:

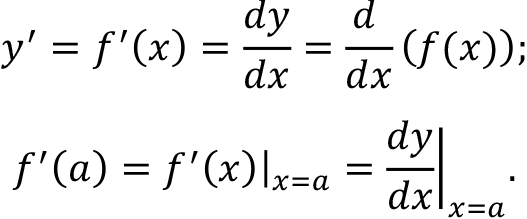
For example, f(x) = x ² + 3x ,

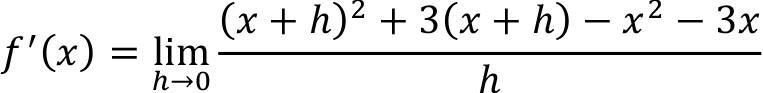
Tangent Line

The slope of the tangent line to the graph of y = f ( x ) at the point ( a, f ( a )) is equal f' ( a ), the equation of this tangent line is

y - a = f '(a)(x- a)

Example: Given graph of the function f(x) = x ² + 3 x , the slope of the tangent line at (1,4) is

f '(1) = 2 · 1 + 3 = 5

and the equation of the tangent line is

y - 4 = 5( x - 1) or y - 5 x + 1 = 0.

Average and Instantaneous Velocity of a Moving Particle

If a particle moves along the x -axis in such a way that its position at time t is f(t) , then its average velocity on some time interval is

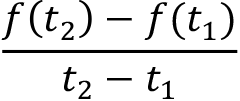
and velocity at any time t is the derivative f '(t) .

Example: The motion of a particle is given by the function f (t) = t ² + 3t. The average velocity on the time interval [1,5] is

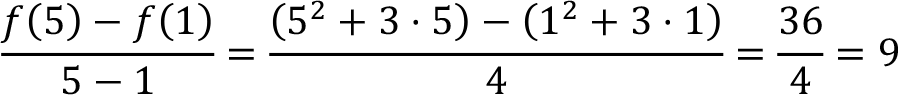
the velocity at instant time t = 2 is f '(2) = 2 · 2 + 3 = 7.

Some Important Derivatives

Using the definition of the derivative and the properties of the limit operation the following derivatives can be calculated as:

• (c)' = 0 (the derivative of a constant function is zero.)
• (x)' = 1
• (x ² )' = 2 x
• (x ³ )' = 3 x ²
• ( )' =
• 
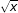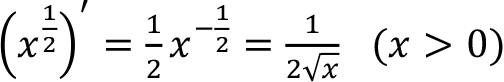
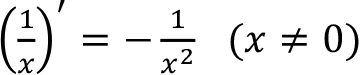
• r ? R, (x ^r )' = r · x ^r-1
• (e ^x )' = e ^x
• (ln x)' =

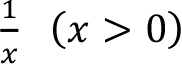
The Derivative Rules

( f ( x ) + g ( x ))' = f' ( x ) + g' ( x ),
( f ( x ) - g ( x ))' = f' ( x ) - g' ( x ),

the product rule:

( f ( x ) . g ( x ))' = f' ( x ) . g ( x ) + f ( x ) . g' ( x ),
( c . f ( x ))' = c. f' ( x ),

the quotient rule

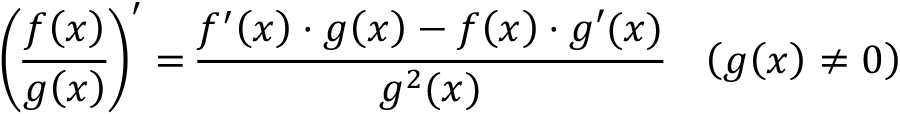
For example,

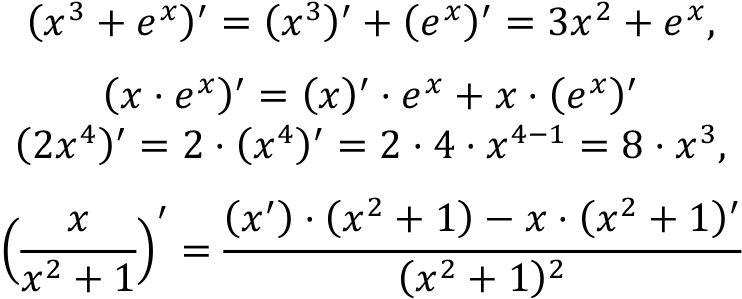
The Chain Rule

In order to calculate the derivatives of more complicated functions the following chain rule can be applied.

If f(x) and g(x) are differentiable then the composite function f ° g(x) = f (g(x)) is also differentiable and

(f (g(x)))' = f' (g(x)) . g'(x).

Here f ' (g(x)) is the derivative of f(x) calculated at the point g(x) .

For example,

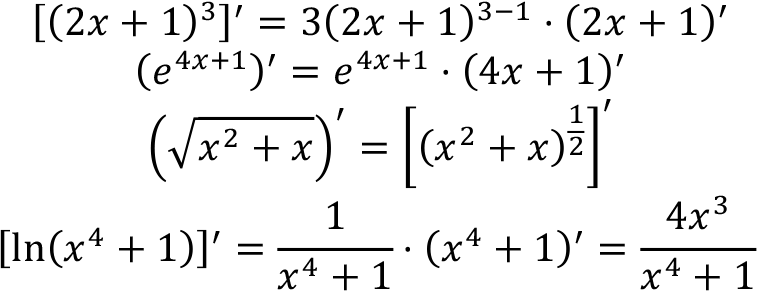
Higher Order Derivatives

If a function f(x) is differentiable, its derivative f'(x) is a function of x . The derivative of the function f'(x) is called the second order derivative of f(x) and is denoted by f''(x) or y ''. If the function f''(x) is differentiable, the derivative of the function f''(x) is called the third order derivative of f(x) and is denoted by f'''(x) or y '''. In the general, n ^th order derivative is denoted by f ⁽ⁿ⁾ (x) or y ⁽ⁿ⁾ provided that the derivative exists.

Examples:

f(x) = x ² , f'(x) = ( x ² )' = 2 x , f''(x) = (2 x )' = 2 , f'''(x) = ( 2 )' = 0.
g(x) = e ^-x
g'(x) = (e ^-x )' = e ^-x . (-x)' = -e ^-x ,
g''(x) = (-e ^-x )' = -e ^-x . (-x)' = e ^-x ,
g'''(x) = -e ^-x .

Applications of Derivatives

Find the equation of the tanget line to the graph of the function y = e ^2x at the point (1, e ² ).

y' = (e ^2x )' = e ^2x . (2x)' = 2e ^2x ,
y' | _x-1 = 2e ^2.1 = 2e ² ,

the equation of the tangent line

y - e ² = 2(x - 1).

Local Extremums and Monotonicity

Given y = f(x) , if f'(a) = 0 then a is called a critical point.

If for all x ? ( a, b ) the inequality f'(x) > 0 is satisfied then f(x) is monotone increasing on ( a, b ) ; if for all x ? ( a, b ) the inequality f'(x) < 0 is satisfied then f(x) is monotone decreasing on ( a, b ).

Example: f(x) = x ² + 4 x . f'(x) = ( x ² + 4)' = 2 x + 4.
2 x + 4 = 0 ? 2 x = -4 ? x = -2

is a critical point,

2 x + 4 > 0 ? 2 x > -4 ? x > -2

that is on the interval (-2, ?) the function f(x) is monotone increasing,

2 x + 4 < 0 ? 2 x < -4 ? x < -2

on the interval (-?, -2) the function f(x) is monotone decreasing.

Second Derivative Test for Local Extrema:

If a is a critical point and the second derivative f''(a) is positive,i.e. f''(a) > 0, then a is a local minimum point.

If f''(a) is negative, i.e. f''(a) < 0, then a is a local maxmimum point.

Example: f(x) = x ³ - 12 x ,
f'(x) = (x ³ - 12 x)' = 3x ² - 12,
f''(x) = (3x 2 - 12 )' = 6x.

Critical points:

3x ² - 12 = 0, 3( x - 2)( x + 2) = 0, x = -2, x = 2.

Interval of increase:

3x ² - 12 > 0, 3( x - 2)( x + 2) > 0, x < -2 and x > 2.

Interval of decrease:

3x ² - 12 < 0, 3( x - 2)( x + 2) < 0, -2 < x < 2.
f''( - 2) = 6 · (-2) = -12 < 0 ? x = -2 is a local maximum point.
f''( 2) = 6 · (2) = 12 > 0 ? x = 2 is a local minimum point.

First Derivative Test for Local Extrema:

If x ₀ is a critical point and f'(x) < 0 to the left of x ₀ and f'(x) > 0 to the right of x ₀ then x ₀ is a local minimum.

If f'(x) > 0 to the left of x ₀ and f'(x) < 0 to the right of x ₀ then x ₀ is a local maximum.

Example: f(x) = 1 - x ² , f'(x) = (1 - x ² )' = -2 x .

f'(x) = 0 ? -2 x = 0 ? x = 0 is a critical point.

Take x = -1 then f'(x) | _{x= - 1} = (-2) · (-1) = 2 > 0 ,
take x = 1 , then f'(x) | _x=1 = (-2) · (1) = -2 < 0 .
Therefore x = 0 is a local maximum.