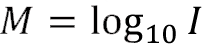Chapter 4: Exponential and Logarithmic Functions

Exponential Functions In this chapter, we study the exponential and logarithmic functions, particularly natural exponential and logarithmic functions and their properties. An exponential function is a function of the form

f:( -?, ?) › (0, ?) ,
f(x) = a ^x

where the base a is a positive constant and the exponent x is the variable. Note that exponential function f(x) = a ^x is defined for all real numbers. Exponential functions obey following identities, which are called “ laws of exponents ”.

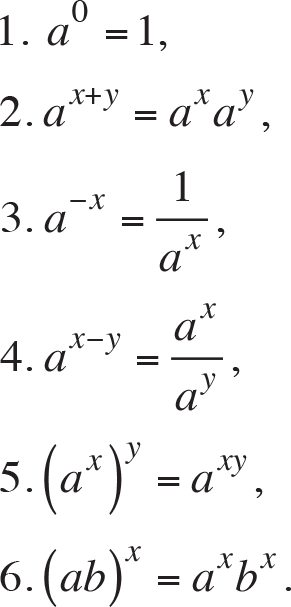
for any real numbers x and y , any positive real numbers a and b .

The behaviour of the graphs of the exponential functions is different for the cases  0 < a < 1  and a > 1 . For  0 < a < 1 , the shapes of graphs of all exponential functions are similar to the following graph

while for a > 1 the shapes of graphs of all exponential functions are similar to the following graph

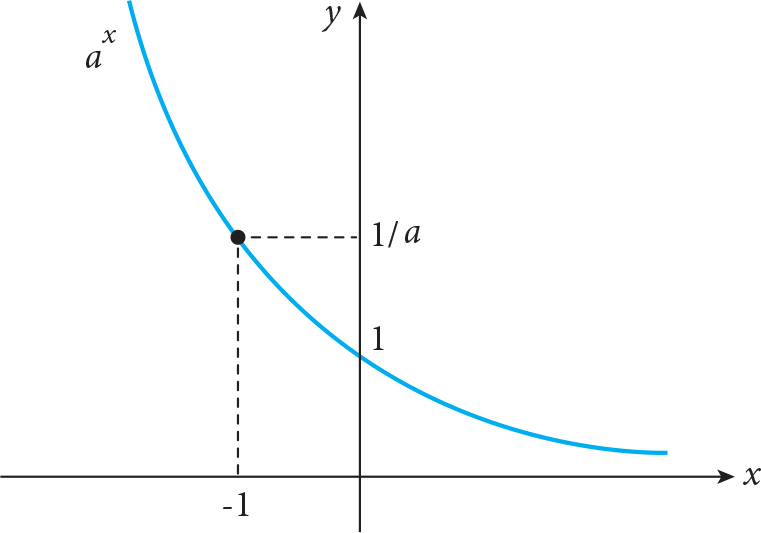
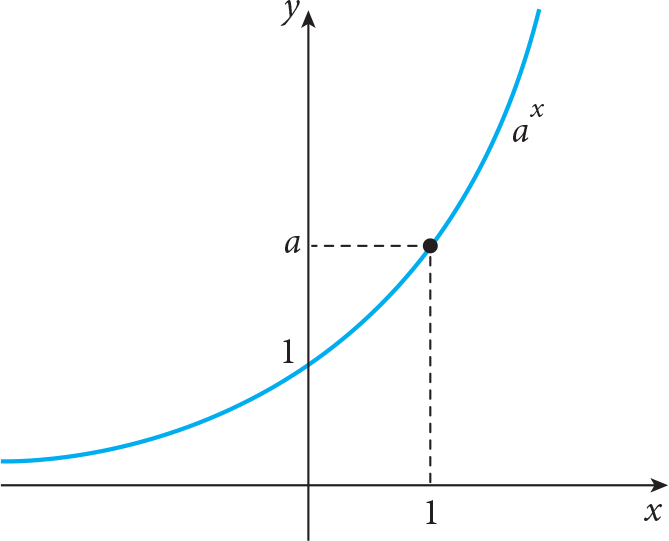
Note that domain of an exponential function is (-?, ?) and range is (0, ?) . In addition, if a > 1 (0 < a < 1 ) , then the exponential function is increasing (decreasing), respectively.

Compound Interest and the Natural Base

When an amount of money is invested in an account, which pays interest, interest is calculated for the first period (be it a day, a week, a month or a year). This interest is then added to the initial amount. Following on from that, the interest for the next period is calculated but is based on the whole figure from the first period. This interest is called compound interest.

As n goes to infinity, 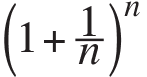approaches

2,718281778 ? .

This number

e ?2,718281778 ?

is called the natural base . The exponential function

e ^x

is called the natural exponential function. The natural exponential function satisfy “ laws of exponents ” as

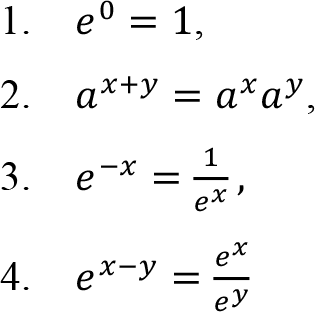
for any real numbers x and y .

Logarithmic Functions

An exponential function a ^x has an inverse function since this function is one-to-one. The inverse function of a ^x is called the logarithmic function with base a and denoted by

g: (0, ?) › (-?, ?)

g(x) = log _a x .

The inverse relation is

y = log _a x if and only if x = a ^y

for x > 0 and 0 < a ? 1.

For  0 < a < 1, the shapes of graphs of all logarithmic functions are similar to the following graph

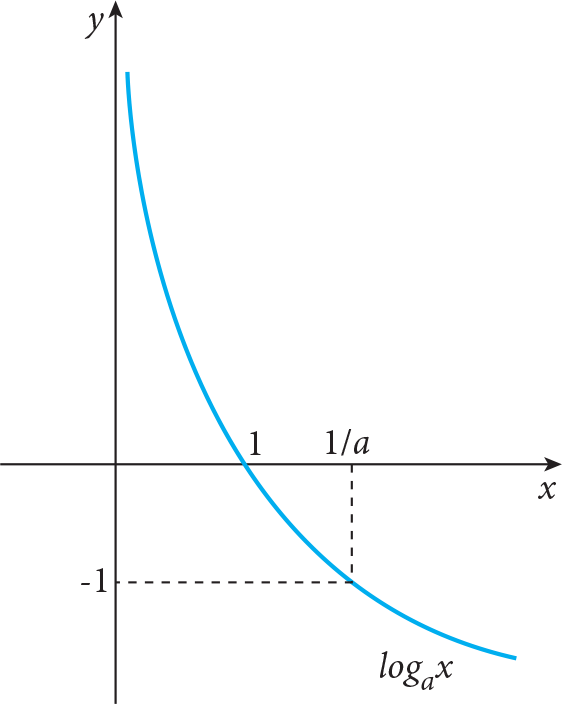
while for a > 1 the shapes of graphs of all logarithmic functions are similar to the following graph

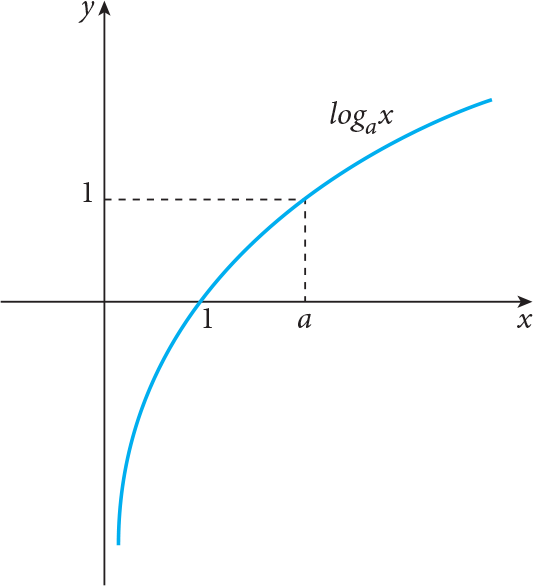
The logarithmic function with base a satisfy following basic properties:

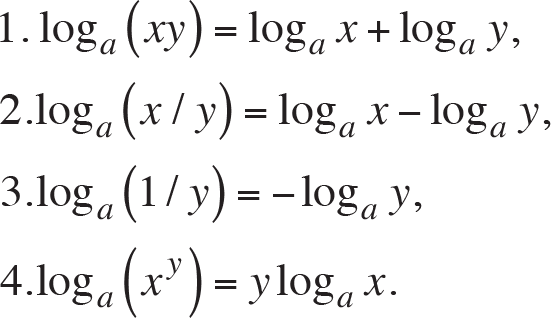
where x and y are positive real numbers. In addition, we express the change-of-base formula as

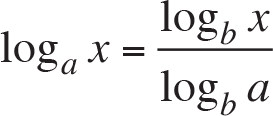
for any positive real numbers x .

The natural logarithmic function is the logarithmic function with base e (inverse function of the natural exponential function) and is denoted by

x > 0

while the common logarithmic function is the logarithmic function with base 10 . The natural logarithmic function obeys above rules, too:

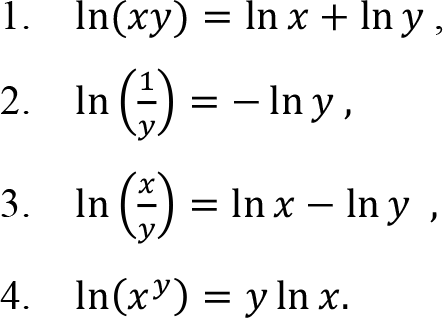
Applications of Exponential and Logarithmic Functions

Some quantities (radioactive substance, bacteria, cells, etc.) decrease or increase at a rate proportional to their amount (exponential growth or decay). The amount of material (or bacteria, cells, etc.) at time t is given as

which is a function of time t . The constants Q ₀ and k are determined by the initial conditions, i.e. the quantities of the given material at t = 0. Thus, the function is fully determined and we can evaluate the sought for quantities asked in the question.

We observe that k is positive for exponential growth problems while k is negative for those of exponential decay.

One of the most important applications of logarithmic models is the evaluation of magnitude of an earthquake. The magnitude of an earthquake measures the energy it releases. The intensity of an earthquake is a measure of the strength of shaking produced by the earthquake at a certain place. On the Richter scale, the magnitude M of an earthquake of intensity I is expressed by the formula