SAĞLIK ALANINDA İSTATİSTİK - Ünite 4: Örnekleme ve Hipotez Testleri Özeti :

PAYLAŞ:

Ünite 4: Örnekleme ve Hipotez Testleri

Örnekleme

İncelenen özellikleri yönünden genellemeler yapılması istenen bir ana kütleden, belli yöntemlerle örneklemin seçilmesi ve bu örneklemin incelenmesi sonucunda hesaplanan istatistiklerin genelleme amacıyla kullanılması işlemlerinden oluşan sürece örnekleme adı verilir

İlgilenilen sonlu ana kütlenin bütün birimlerine ilişkin bilgilerin sistemli olarak elde edilmesi ve kaydedilmesi sürecine tam sayım denilir. Tam sayım sonucunda elde edilen bilgiler, veri derleme hatası işlenmediği takdirde kesin bilgilerdir.

Seçilen örneklemdeki birim sayısının, ana kütledeki birim sayısına oranına örnekleme oranı adı verilir ve f = n / N eşitliği yardımıyla hesaplanır.

Örneklemin çekildiği sonlu bir ana kütledeki birimlerin yer aldığı listeye örnekleme çerçevesi adı verilir. Örneğin, büyük bir firmada çalışan tüm elemanlar arasından bir örneklem çekmek istenildiğinde, firmanın telefon rehberinde yazılı isimler arasından seçim yapılıyor ise bu telefon rehberi örnekleme çerçevesi olacaktır. Örnekleme çerçevesinin tanımlanan ana kütledeki birimleri olabildiğince içermesi gerekir.

Ana kütleyi oluşturan her bir birime ana kütle birimi adı verilir. Ana kütleden seçilen örneklemi oluşturan elemanlara örnekleme birimi adı verilir. Örnekleme birimi bir tek ana kütle biriminden oluşabileceği gibi birden çok ana kütle biriminden de oluşabilir.

Verilerin toplandığı ve istatistiklerin derlendiği birime gözlem birimi adı verilir. Örnekleme birimi ile gözlem birimi aynı olabileceği gibi farklı da olabilir. Örneğin, ilköğretim öğrencileri üzerine yapılacak bir araştırmada bilgiler öğrencilerden toplanıyorsa her bir öğrenci bir gözlem birimidir.

Bir ana kütle parametresinin olası değerinin belirlenmesinde kullanılan örneklem istatistiğine tahminci adı verilir ve her tahminci bir rassal değişkendir. Örneğin, ana kütle aritmetik ortalamasının tahmincisi olarak örneklem aritmetik ortalaması kullanılabilir.

Örnekleme yöntemi uygulanan istatistiksel araştırmalarda birincisi sistematik hata, ikincisi ise rassal hata (örnekleme hatası) olmak üzere iki tür hata söz konusu olur. Örneklem istatistikleri, N sayıda birimden oluşan ana kütleden seçilen n birimlik örneklemden elde edilen veriler kullanılarak hesaplandığı için ana kütle parametresi ile örneklem istatistiği arasında belli miktarda bir fark ortaya çıkar. Bu farka örneklemede rassal hata ya da örnekleme hatası adı verilir. Örneklem istatistiği ile ana kütle parametresi arasındaki farkların alabileceği değerler negatif, sıfır ya da pozitif olabileceği için, bu farkların ortalaması hesaplanırken kareli ortalamadan yararlanılır. Hesaplanan bu değere de, örneklem istatistiğinin standart hatası adı verilir. Standart hata ne kadar küçülürse örneklem istatistiği ana kütle parametresine o ölçüde yakın olacaktır.

Ana kütlede yer alan tüm örneklem birimlerinin belirli olasılıklarla örnekleme seçildiği yöntemlere olasılıksal ya da rassal örnekleme yöntemleri adı verilir. Bu yöntemlerde, her bir örnekleme biriminin belli bir seçilme olasılığı bulununur. Maliyet, zaman, işgücü vb. gibi fiziki kaynaklar yeterli düzeyde ise uygulamalarda her zaman olasılıksal örnekleme yöntemleri tercih edilmelidir. Çünkü olasılıksal örnekleme yöntemleri ile seçilen örneklemin ana kütleyi ne kadar temsil edebildiği tespit edilebilir.

Uygulamalarda en sık kullanılan ve tüm olasılıksal örnekleme yöntemlerinin temelini oluşturan örnekleme yöntemidir. Basit Rassal Örnekleme (BRÖ) yönteminin en önemli özelliği hem ana kütlede yer alan tüm birimlerin hem de ana kütleden seçilebilecek tüm örneklemlerin seçilme şanslarının eşit olmasıdır. BRÖ yönteminde seçilebilecek olası örneklem sayısı ise _N C _n ile verilir.

Sistematik Örnekleme (SÖ), BRÖ’nin örneklem seçimini kolaylaştıran özel bir türüdür. Araştırmada incelenecek değişkenler bakımından ana kütle birimlerinin homojenlik gösterdiği durumlarda genellikle SÖ yöntemi uygulanır.

Tabakalı Örnekleme (TÖ) yönteminin aslı, ana kütlenin araştırmanın konusunu oluşturanmbir ya da daha fazla değişken bakımından çeşitli alt gruplara bölünmesi ve her bir altmgruptan ayrı ayrı örneklem çekilmesine dayanır.

Örnekleme birimlerinin birden çok ana kütle biriminden oluştuğu olasılıksal örneklemeye Küme Örneklemesi (KÖ), her bir örnekleme birimine de bir küme adı verilir. KÖ yönteminde, seçilen kümeler eşit ya da farklı sayıda ana kütle birimi içerebilir. Bu yöntemde ana kütle alt gruplara bölünür ve bu gruplar üzerinden örneklemeye geçilerek örnekleme giren grupların tamamı alınır.

Ana kütledeki bazı birimlerin seçilen örneklemde yer alma şansının bulunmadığı ya da seçilme olasılığının tam olarak belirlenemediği örnekleme yöntemlerine olasılıksal olmayan örnekleme yöntemleri adı verilir. Olasılıksal olmayan örnekleme yöntemlerine, genellikle olasılıksal örnekleme yöntemleri kullanmanın mümkün olamadığı durumlarda başvurulur. Uygulamalarda en sık kullanılan olasılıksal olmayan örnekleme yöntemleri: Kolayda Örnekleme, Kota Örneklemesi, Kartopu Örneklemesi ve Karar Örneklemesi’dir.

Bir ana kütleden seçilebilecek tümü n birimlik olası bütün örneklemler çekilip hepsinden ayrı ayrı istatistik hesaplandığında söz konusu istatistiklerin dağılımına hesaplanan istatistiğin örnekleme dağılımı adı verilir.

N büyüklüğündeki bir ana kütleden n birimlik 100 adet örneklem seçilmiş olsun ve bu örneklemlerin her biri için aynı x değişkenine ait aritmetik ortalamalar hesaplansın. 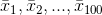$\bar{x}_{1}, \bar{x}_{2},..., \bar{x}_{100}$ örneklem ortalamaları, ortalamanın örnekleme dağılımını oluşturur.

Ana kütleden n birimlik olası bütün örneklemler iadeli seçim yöntemi ile çekildiğinde, belirlenen değişken için örneklem ortalamalarının dağılımının iki önemli özelliği bulunur:

Örneklem ortalamalarının ortalaması ana kütle ortalamasına eşittir. ( µ! = µ)
Örneklem ortalamalarının standart sapmasının değeri, ana kütle standart sapmasından küçüktür ve ana kütle standart sapmasının örneklem büyüklüğünin kareköküne bölünmesi yoluyla hesaplanır.
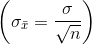
$\left ( \sigma _{\bar{x}}=\frac{\sigma }{\sqrt{n}} \right )$

Ortalamalarının örnekleme dağılımının üçüncü özelliği, dağılım biçimine ilişkin olarak verilir ve istatistikte bu özellik Merkezi Limit Teoremi adı verilen teoremle açıklanır. Bu teoreme göre; ortalaması µ ve standart sapması ? olan herhangi bir ana kütleden iadeli seçimle çekilen örneklem ortalamalarının dağılımı, n büyüdükçe, ortalaması µ ve standart sapması 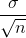$\frac{\sigma }{\sqrt{n}}$ olan normal dağılıma yaklaşır

Ana kütle çok büyük ya da sonsuz ana kütle olduğunda, bu ana kütleden iadeli ya da iadesiz seçim yöntemiyle seçilen örneklemler için ortalamanın standart hatası 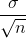$\frac{\sigma }{\sqrt{n}}$ ile hesaplanır. Uygulamalarda iadeli seçimli örnekleme çok fazla uygulanmadığından, sonlu bir ana kütleden iadesiz seçimle çekilen örneklemler için ortalamanın ya da oranın standart hatası hesaplanırken, düzeltme terimi adı verilen bir ifade kullanılır. N; ana kütle çapı ve n; örneklem büyüklüğü olmak üzere düzeltme terimi; 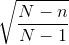$\sqrt{\frac{N-n}{N-1}}$ formülü ile hesaplanır. Düzeltme terimi, küçük bir ana kütleden nispeten büyük bir örneklem çekildiğinde kullanılır. Çünkü bu durumda örneklem ortalaması ana kütle ortalamasına daha yakın sonuçlar vereceği için yapılan tahmindeki hata miktarı daha düşük olacaktır.

Nokta ve Aralık Tahminlemesi

Örneklem birimlerinden elde edilen veriler genellikle, söz konusu rassal değişkenin aldığı sayısal değerlerdir. Dolayısıyla örneklemede ana kütle parametreleri, örneklemden hesaplanan istatistikler yardımıyla tahmin edilir.

İstatistiksel çıkarım problemleri tahminleme ve hipotez testleri olmak üzere iki kısımda incelense de temelde bunların bütünü karar alma problemini oluşturur. Bu iki süreç arasındaki temel fark, tahminleme probleminde parametrenin ya da parametrelerin aldığı değerleri belirlememiz gerekirken hipotez testlerinde parametrelerin aldığı belirli değerleri kabul ya da reddetme kararını vermemiz gerekir. Bir örneklemden elde edilen bilgiden yararlanarak parametrenin aldığı değeri tahmin etme süreci olan tahminleme, çıkarımsal istatistiğin önemli bir bölümünü oluşturur.

Örneklem istatistikleri yardımıyla ana kütle parametrelerinin tahmin edilmesi, nokta tahminlemesi ve aralık tahminlemesi olmak üzere iki şekilde gerçekleştirilir.

Bir ana kütle parametresinin tek bir sayı olarak tahmininde kullanılan örneklem istatistiği değerine nokta tahmini adı verilir.

Ana kütle parametresinin içerisinde yer alacağı tahmin edilen ve belli bir güven düzeyine göre belirlenen sayısal değerler aralığına güven aralığı adı verilir. Belli bir aralığın ana kütle parametresini içermesi olasılığına güven düzeyi denilir.

Bir istatistiğin hesaplanmasında kullanılan değişebilen değerlerin sayısına serbestlik derecesi denir.

Hipotez Testleri

Hipotez kavramı, kuramsal olarak varsayılan ve önceden yapılmış bir dizi gözleme ya da tecrübeye dayanarak ortaya atılan, doğruluğu bilimsel araştırmalarla sınanmaya çalışılan bir önermedir. Bu bağlamda hipotezler, olaylar arasında ilişki kuran ve bu olayların nedenlerini araştırmak amacıyla planlanan önermelerdir ve bu önermenin doğruluğu bilimsel yöntemlerle denetlenebilir olmalıdır.

İstatistiksel hipotez ise bir ya da daha fazla ana kütleye ilişkin olarak ileri sürülen ve teorik bir dağılım varsayımı altında, parametrik değerin belirli bir değere eşit olduğunu veya iki ya da daha fazla ana kütle parametresinin birbirlerine eşit olduğunu belirten ve geçerliliği istatistiksel testlerle denetlenen bir önermedir.

İstatistiksel hipotez testi sürecinde izlenmesi gereken temel adımlar;

Hipotezlerin kurulması
Anlam düzeyinin seçilmesi
Red bölgesinin belirlenmesi
Kritik değerin bulunması
Gerekli test istatistiğinin hesaplanması
İstatistiksel kararın verilmesi şeklindedir.

Sıfır (Yokluk) Hipotezi (H ₀ ), tek bir ana kütle parametresinin belli bir değere eşit olduğunu ya da iki ana kütleye ilişkin parametrelerin birbirlerine eşit olduğunu ileri süren istatistiksel hipotezdir.

Karşıt (Alternatif) Hipotez (H ₁ ), tek bir ana kütle parametresinin belli bir değerden farklı olduğunu (“?” eşit olmadığını, “>” büyük olduğunu, “<" küçük olduğunu) ya da iki ana kütleye ilişkin parametrelerin birbirlerinden farklı olduğunu (“?”, ”>”, ”<”) ileri süren istatistiksel hipotezdir.

Örneklem istatistiği ile ana kütle parametresi arasındaki farkın standartlaştırılması sonucu elde edilen karşılaştırma ölçütüne test istatistiği adı verilir.

Gerçekte H ₀ hipotezi doğru iken test sonucunda yanlış karara varılıp reddedilirse yapılan bu hataya 1. tip hata ya da ?-hatası adı verilir. Gerçekte H ₀ hipotezi yanlış iken test sonucunda yanlış karara varılıp kabul edilirse yapılan bu hataya da 2. tip hata ya da ß-hatası adı verilir.

1. tip hatayı işleme riskine razı olabileceğimiz maksimum olasılığa testin anlam düzeyi denilir ve ? simgesi ile belirtilir. Uygulamalarda en sık kullanılan anlam düzeyleri ? = 0,05, ? = 0,01, ve ? = 0,001 değerleridir. Ayrıca 1 – ?’ya güven düzeyi adı verilir ve hipotez testinin güvenilirlik düzeyini ifade eder. 1 – ß’ya ise testin gücü denilir.

Test istatistiğinin örnekleme dağılımı üzerinde, H ₀ hipotezini reddetmek üzere tanımlanan bölgeye red bölgesi adı verilir. Red bölgesinin büyüklüğü ? anlam düzeyine eşittir.

Test istatistiğinin örnekleme dağılımında, H ₀ hipotezinin reddedilmeye başladığı noktaya kritik değer adı verilir.

Varyans Analizi

İkiden fazla ana kütle ortalamasının karşılaştırılmasında Varyans Analizi (ANOVA) yöntemi kullanılır. ANOVA ile dağılımların toplam değişkenliğini çeşitli bileşenlere ayırma yöntemi yardımıyla bağımsız değişkenlerin bağımlı değişkenler üzerindeki etkileri incelenebilmektedir. İki ana kütle ortalamaları karşılaştırması için geliştirilen istatistiksel yöntemlerin, ikiden fazla ana kütle ortalamasının karşılaştırmasına genellenmesi Tek-Yönlü Varyans Analizi olarak adlandırılır.