AOF.SORULAR.NET
aof.sorular.net SAĞLIK KURUMLARINDA OPERASYON YÖNETİMİ SAĞLIK KURUMLARINDA OPERASYON YÖNETİMİ - Ünite 2: Sağlık Yönetiminde Öngörü Özeti

SAĞLIK KURUMLARINDA OPERASYON YÖNETİMİ - Ünite 2: Sağlık Yönetiminde Öngörü Özeti :

PAYLAŞ:

Ünite 2: Sağlık Yönetiminde Öngörü

Giriş

Tüm sağlık yöneticileri bulundukları faaliyet alanlarında stratejik düzeyden operasyonel düzeye kadar geniş bir skalada kararlar verirler. Karar sürecinde gerçekleşen geçmiş verilerden yararlanarak gelecek hakkında öngörüde bulunmak, doğru teknikler kullanıldığında belirsizliği azaltacaktır. Ancak belirsizlik nedeniyle öngörü modellerinde mutlaka hata payı da bulunacaktır. Önemli olan hazırlanan modeller ile hata payını azaltmaktır. Ayrıca hatanın büyümemesi için uzun vadeden ziyade kısa vadede tahminlerde bulunmak gerekir. Sağlık hizmetlerinin her alanında geleceğe yönelik öngörüler yapılırken öngörü tekniklerinden yararlanılmaktadır. Bu uygulama alanlarına örnek olarak aşağıdaki problem alanları verilebilir:

  • Hasta talebi öngörüsü,
  • Gelir-gider öngörüleri,
  • Sağlık personeli gereksinimi öngörüleri,
  • Kullanılacak malzeme öngörüleri,
  • Ameliyathane gereksinimi öngörüleri,
  • Yatak gereksinimi öngörüleri,
  • Pazar payı öngörüleri.

Zaman Serileri ile Öngörü

Zaman serisi, bir değişkenin zaman içerisinde aldığı değerlerin kümesi olarak tanımlanabilir. Geçmiş dönemdeki hasta sayıları, gelirleri, tıbbi personel sayıları zaman serilerine örnek olarak verilebilir. Sağlık işletmeleri zaman serilerini kullanarak gelecek ile ilgili öngörülerde bulunurlar.

Zaman serisi incelenirken öncelikle verinin aşağıda tanımlanan özellikleri gözden geçirilmelidir:

  • Durağan veri: Zaman serisini oluşturan değişkenin zaman içinde belli bir yönde anlamlı bir hareketi yoktur.
  • Durağan olmayan veri : Zaman serisini oluşturan değişkenin zaman içinde yukarı ya da aşağı yönde anlamlı bir hareketi bulunmaktadır.
  • Mevsimsel veri: Zaman serisini oluşturan değişken zaman içinde belirli aralıklarda tekrarlayan bir kalıp izlemektedir.

Durağan Modeller

Zaman serisini oluşturan değişkenin zaman içinde belli bir yönde anlamlı bir hareketi yok ise, seri durağan bir yapıdadır ve durağan yapıyı açıklayan modeller ile analiz edilir. Hareketli ortalama, ağırlıklı hareketli ortalama ve üstel düzleme teknikleri durağan veri için kullanılabilecek tekniklerdendir.

Hareketli Ortalama: Hareketli ortalamalar, zaman serisinin genel kalıbını bozan kısa süreli tesadüfi dalgalanmaları yumuşatmak için geliştirilmiştir. Bu teknik, basitliği nedeniyle yaygın olarak kullanılmaktadır. Bu teknikle t+1 döneminin öngörülen zaman serisi değeri önceki k dönemin ortalamasıdır.

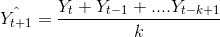
\hat{Y_{t+1}}=\frac{Y_{t}+Y_{t-1}+....Y_{t-k+1}}{k}

k çok küçük alındığında, elde edilen hareketli ortalama serisi orjinal zaman serisini çok yakından takip eder, ancak halen ana kalıbı bozan tesadüfi dalgalanmalar içerir. k çok büyük alındığında ise, tesadüfi dalgalanmalar büyük ölçüde elimine edilmesine karşın elde edilen hareketli ortalama serisi orjinal zaman serisini yakından takip etmez.

Ağırlıklı Hareketli Ortalama: Hareketli ortalamalar ile öngörü yapılırken, hesaplamaya katılan k dönemin de öngörüde ağırlığı aynı alınır. Ancak karar verici dönemlerin ağırlıklarını farklı almak isteyebilir. Özellikle öngörü yapılacak dönemlere yakın dönemlerin ağırlıklarının, uzak dönemlere göre daha fazla olması genellikle istenilen bir durumdur.

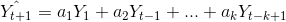
\hat{Y_{t+1}}= a_{1}Y_{1}+a_{2}Y_{t-1}+...+a_{k}Y_{t-k+1}

Üstel Düzleme: t+1 döneminin öngörülen zaman serisi değeri ( t 1 Yˆ + ), aşağıdaki ifade ile hesaplanır.

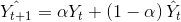
\hat{Y_{t+1}}= \alpha Y_{t}+\left ( 1-\alpha \right )\hat{Y_{t}}

Bu ifadeye göre t+1. dönemin öngörülen değeri, bir önceki dönemin gerçekleşen (t Y) ve öngörülen (t Yˆ) değerlerinin ? ile ağırlıklandırılmış toplamlarına eşittir. Düzleme sabiti olarak adlandırılan ? , 0 ile 1 arasında bir değer alır. ? ’ya 1’e yakın bir değer atanması son veriye ağırlık verirken, 0’a yakın bir değer atanması daha eski veriye daha çok ağırlık verilmesi anlamına gelmektedir.

Mevsimsellik

Durağan bir zaman serisi verisinde düzenli olarak tekrarlayan bir dalgalanma kalıbı varsa, mevsimsel yapıda bir seri olduğu söylenebilir. Mevsimsel etki toplamsal ya da çarpımsal yapıda olabilir.

Toplamsal Mevsimlik Yapıda Durağan Model: Toplamsal mevsimlik yapıya sahip durağan zaman serilerinde aşağıda gösterilen model kullanılır:

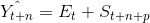
\hat{Y_{t+n}}=E_{t}+S_{t+n+p}

Bu modelde;

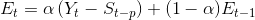
E_{t}= \alpha \left (Y_{t}-S_{t-p})+(1-\alpha )E_{t-1}

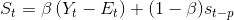
S_{t}= \beta \left (Y_{t}-E_{t})+(1-\beta )s_{t-p}

Görüldüğü gibi, t+1. dönemin öngörüsünü bulan ifade Et ve St terimlerinden oluşmaktadır. Et, zaman serisinin t dönemindeki düzeyini, St de, t dönemindeki mevsimsel faktörü göstermektedir. ? ve ß , 0 ile 1 arasında değer alan sabitlerdir. p ise bulunulan mevsimsel dönemi gösteren sabittir. p değeri haftalık veri için 7, aylık veri için 12, üç aylık veri için de 4 olarak alınır. Aşağıda verilen örnek ile toplamsal mevsimlik yapıya sahip durağan zaman serileri uygulaması yapılmıştır.

Çarpımsal Mevsimlik Yapıda Durağan Model: Çarpımsal mevsimlik yapıya sahip durağan zaman serilerinde ise aşağıda gösterilen model kullanılır:

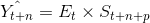
\hat{Y_{t+n}}= E_{t}\times S_{t+n+p}

Bu modelde;

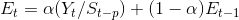
{E_{t}}=\alpha (Y_{t}/S_{t-p})+(1-\alpha )E_{t-1}

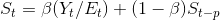
S_{t}= \beta (Y_{t}/E_{t})+(1-\beta )S_{t-p}

Bu modelde de t+1. dönemin öngörüsünü bulan ifade Et ve St terimlerinden oluşmaktadır. Et, zaman serisinin t dönemindeki düzeyini, St de, t dönemindeki mevsimsel faktörü göstermektedir. ? ve ß , 0 ile 1 arasında değer alan sabitlerdir. p ise bulunulan mevsimsel dönemi gösteren sabittir.

Trend Modelleri

Zaman serisi verisi içinde belli bir dönem boyunca artan ya da azalan bir yön gözlemleniyorsa, seri durağan değildir ve bir trende sahiptir. Bu kısımda durağan olmayan zaman serileri için uygun öngörü teknikleri açıklanacaktır.

Doğrusal Regresyon Modeli: Doğrusal trende sahip bir zaman serisinin regresyon modeli şu şekildedir:

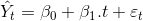
\hat{Y}_{t}= \beta _{0}+\beta _{1}.t+\varepsilon _{t}

Bu regresyon eşitliğinde bağımlı değişken olan t Yˆ , t bağımsız değişkeninin doğrusal bir fonksiyonudur. Fonksiyondaki ß0 + ß1 t ifadesi, zaman serisinin sistematik hareketini, t ? ise sistematik olmayan hareketini göstermektedir. İdeal durumda t ? ’nin ortalama değerinin 0 olması beklenir.

Kuadratik Regresyon Modeli: Kuadratik trende sahip bir zaman serisinin regresyon modeli şu şekildedir:

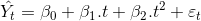
\hat{Y_{t}}=\beta _{0}+\beta _{1}.t+\beta _{2}.t^{2}+\varepsilon _{t}

Bu regresyon eşitliğinde bağımlı değişken olan t Yˆ , t bağımsız değişkeninin kuadratik bir fonksiyonudur. Fonksiyondaki ß0 + ß1t + ß2t 2 ifadesi, zaman serisinin sistematik harketini, t ? ise sistematik olmayan hareketini göstermektedir.

Holt Metodu : Holt metodu doğrusal trend izleyen zaman serilerinde kullanılan tekniklerden biridir. Teknik, çift ÜD tekniği olarak da adlandırılmaktadır. Holt metodu ile öngörüde aşağıdaki model kullanılır:

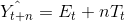
\hat{Y_{t+n}}= E_{t}+nT_{t}

Bu modelde;

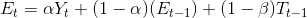
{E_{t}}= \alpha Y_{t}+(1-\alpha )(E_{t-1})+(1-\beta )T_{t-1}

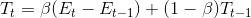
T_{t}= \beta (E_{t}-E_{t-1})+(1-\beta )T_{t-1}

Görüldüğü gibi t+1. dönemin öngörüsünü bulan ifade Et ve Tt terimlerinden oluşmaktadır. Et, zaman serisinin t dönemindeki beklenen düzeyini, Tt de, t dönemindeki beklenen trendi göstermektedir. ? ve ß , 0 ile 1 arasında değer alan sabitlerdir.

Holt-Winter Metodu (Toplamsal Mevsimlik Yapıda): Durağan olmayan zaman serileri, trend bileşeninin yanısıra mevsimsel faktörleri de içeriyorsa Holt-Winter metodu ile öngörü yapılabilir. Önceki kısımlardan hatırlanacağı gibi, mevsimsel etki toplamsal ya da çarpımsal yapıda olabilir. Toplamsal mevsimlik yapıda Holt-Winter metodu ile öngörüde aşağıdaki model kullanılır:

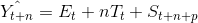
\hat{Y_{t+n}}= E_{t}+nT_{t}+S_{t+n+p}

Bu modelde;

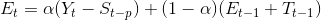
{E_{t}}= \alpha (Y_{t}-S_{t-p})+(1-\alpha )(E_{t-1}+T_{t-1})

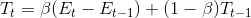
T_{t}= \beta (E_{t}-E_{t-1})+(1-\beta )T_{t-1}

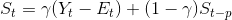
S_{t}= \gamma (Y_{t}-E_{t})+(1-\gamma )S_{t-p}

Görüldüğü gibi, t+1. dönemin öngörüsünü bulan ifade Et, Tt ve St terimlerinden oluşmaktadır. Et, zaman serisinin t dönemindeki beklenen düzeyini, Tt, t dönemindeki beklenen trendi, St de, mevsimlik etkiyi göstermektedir. ?, ß ve ? , 0 ile 1 arasında değer alan sabitlerdir.

Holt-Winter Metodu (Çarpımsal Mevsimlik Yapıda): Durağan olmayan zaman serilerinde, trend bileşeninin yanısıra çarpımsal mevsimsel faktörleri de içeren Holt Winter metodu ile öngörüde aşağıdaki model kullanılır:

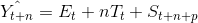
\hat{Y_{t+n}}= E_{t}+nT_{t}+S_{t+n+p}

Bu modelde;

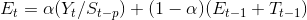
E_{t}= \alpha (Y_{t}/S_{t-p})+(1-\alpha )(E_{t-1}+T_{t-1})

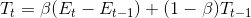
T_{t}= \beta (E_{t}-E_{t-1})+(1-\beta )T_{t-1}

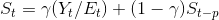
S_{t}= \gamma (Y_{t}/E_{t})+(1-\gamma )S_{t-p}

Görüldüğü gibi, t+1. dönemin öngörüsünü bulan ifade Et, Tt ve St terimlerinden oluşmaktadır. Et, zaman serisinin t dönemindeki beklenen düzeyini, Tt, t dönemindeki beklenen trendi, St de, mevsimlik etkiyi göstermektedir. ? ,ß ve ? , 0 ile 1 arasında değer alan sabitlerdir.