Ünite 3: İş, Enerji, Güç ve Momentum

Giriş

Günlük hayatımız içerisinde bazı faaliyetlerimizi açıklamak için kullandığımız iş ve güç sözcükleriyle, bu kavramların fizik bilimindeki karşılıkları birbirinden farklıdır. Örneğin yazı yazarken veya konuşurken bir enerji harcanmasına rağmen fizikte bu tip aktiviteler iş olarak tanımlanmaktadır.

İş

Durmakta olan bir cisim üzerine bir kuvvet uygulandığında cisim yer değiştiriyorsa bu kuvvet cisim üzerinde iş yapmıştır. Benzer şekilde sabit hızla hareket eden bir cisim üzerine bir kuvvet uygulandığı andan itibaren cismin mevcut hızı veya yer değiştirme doğrultusu değişiyorsa yine bir işten bahsedilebilir. Bunun karşın, duran veya hareket eden cisim üzerine bir kuvvet uygulandığında hızında veya yer değiştirme doğrultusunda bir değişiklik yok ise bir işten bahsedilemez. Kitabınızın 61. sayfasında yer alan Şekil 3.1.’deki A konumunda bulunan bir cisim üzerine kuvvetini uygulayalım. Cisim bu kuvvetin etkisiyle 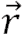kadar yer değiştirerek B konumuna gelmiş olsun. Bu durumda 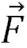kuvvetinin yaptığı iş aşağıdaki eşitlikle tanımlanır (W):

= .
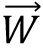W = Frcos (?)

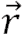Burada a, kuvvet ( ) ile yer değiştirme ( ) vektörleri arasındaki açıdır.

Buna göre;

• Cismin yer değiştirmesi uygulanan kuvvetle aynı yönde değişiyorsa ? açısı dar açı olacağından, cos? değeri pozitif olur, bu nedenle de iş pozitif değer alır.
• Cismin yer değiştirmesi uygulanan kuvvetin yönüne göre ters yönde ortaya çıkıyorsa ? açısı geniş açı olacağından cos ? değeri negatif olur, bu nedenle iş negatif değer alır.
• Cismin yer değiştirmesi ile uygulanan kuvvet arasındaki açı dik ise bu kuvvetin yaptığı işten bahsedilemez.

SI birim sisteminde F(N) ve r (m) olarak alındığında işin birimi (N.m) veya joule (J)’dur. CGS birim sisteminde F(dyne) ve r (cm) olarak alındığında ise işin birimi (dyne.cm) veya erg’dir. Birimler arasında çevrim yapılmak istendiğinde 1N= 10 ⁵ dyne ve 1 joule= 10 ⁷ erg olacak şekilde kullanılır.

İş skaler bir nicelik olduğundan, cisim üzerine birden fazla kuvvet uygulanması durumunda toplam iş, her bir kuvvetin yaptığı işin toplamına eşittir.

Doğru Boyunca Sabit Bir Kuvvetin Yaptığı İş

Kitabınızın 62. sayfasında yer alan Şekil 3.3’te görüldüğü gibi sürtünmeli ve yatay bir düzlemde duran cisim üzerine, hareket boyunca hem büyüklük hem de yön olarak değişmeden kalan 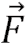₁ ve 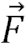₂ gibi farklı iki kuvvet etki etsin. Bu kuvvetlerin etkisi ile cisim yatayda kadar yer değiştirsin. Bu cisim üzerinde yapılan toplam işi bulmak için, öncelikle cisim üzerine etki eden tüm kuvvetlerin yönlerini ve büyüklüklerini ayrı ayrı belirtilmesi gerekir. Bu sistemdeki cisim m kütlesinden dolayı yerçekimi ivmesinden kaynaklanan bir ağırlığına sahiptir. Öte yandan düzlemin cisme uyguladığı 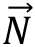tepki kuvveti vardır. Son olarak da cisim, kuvvetlerin etkisi ile hareketlenmesi esnasında hareket yönünün tersine bir 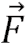_S sürtünme kuvvetine maruz kalır. Toplam işi hesaplamak için cisim üzerine etki eden tüm bu kuvvetlerin yaptığı işi ayrı ayrı hesaplamak, sonra bunları cebirsel olarak toplamak en uygun yöntemdir. ₁ kuvvet vektörü ile yer değiştirme vektörü aynı yönlüdür dolayısıyla aralarındaki açı 0°’dir. Kuvvetlerin yaptığı işler; kitabınızın 63. sayfasında yer almaktadır. Cisim üzerinde iş yapan kuvvetler cismin hareketi doğrultusundaki kuvvet bileşenleridir. Harekete dik doğrultudaki kuvvet bileşenleri ise cisim üzerinde herhangi bir iş yapmaz.

Örn: Bir çiftçi saman yüklü römorkunu şekildeki gibi yerle 37°’lik açı yapacak şekilde traktörüne bağlıyor. Çiftçi 100 N ağırlığındaki yükü, 200 N’luk sabit bir kuvvetle, 20 m’lik mesafeye kadar çekiyor. Bu süreç içinde römorka etki eden sürtünme kuvveti 50 N olduğuna göre yapılan toplam işin kaç joule olacağını bulunuz.

Bu problemin çözümünde cisim üzerine etki eden tüm kuvvetler ayrı ayrı ele alınıp yaptıkları işler hesaplanacaktır. Toplam işi bulmak için de her birinin yaptığı işler cebirsel olarak toplanacaktır. Şekil 3.5’teki diyagramda görüldüğü üzere Newton’un III. yasasına göre cismin ağırlığı ile yerin cisme uyguladığı kuvvet birbirine eşittir (W=N). Hem kuvvetlerin yönü hareket doğrultusuna dik olduğundan hem de kuvvetlerin toplamının sıfır olmasından dolayı, bu kuvvetler tarafından yapılan iş sıfırdır. Traktörün uyguladığı kuvvetinin yaptığı iş;

W _T = Fd cos (?)
W _T = 200.20 cos (37)
W _T = 4000.0,8
W _T = 3200 Nm
W _T = 3200 J

olarak hesaplanır. _S sürtünme kuvvetinin yaptığı iş ise kuvvet hareket yönünün tersi yönde olduğundan dolayı negatif değer alır, yani sürtünme kuvveti traktörün römorku çekmek için yaptığı işten pay alır.

Bir Doğru Boyunca Kuvvetlerin Yaptığı İş: Grafiksel Yaklaşım

Aşağıdaki bölümde bir doğru boyunca farklı zaman veya yer değişmeler boyunca kuvvetlerin yaptığı işin verilen kuvvet-yol grafikleri ile elde edilmesiyle ilgili örnek verilecektir.

Örn: Sürtünmesiz yatay düzlem üzerinde durmakta olan 2 kg’lık bir A cismine, şekildeki gibi, 0-2 m aralığında 10 N’luk, 2-6 m aralığında 10 N’dan başlayarak 20 N’a kadar artan ve 6-8 m aralığında -10 N’dan 0 N’a kadar artan (- işareti kuvvetin ters yönde uygulandığını gösterir), kuvvetler etki etsin. 8 m’lik yolun sonunda yapılan toplam iş nedir?

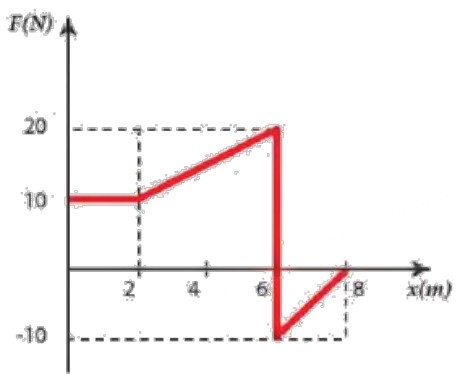
Kuvvet-yol grafiği verilen sorularda öncelikle bölgelere ayırma işlemini yapmalıyız. Bu işlemde dikkat edilmesi gereken en önemli nokta, kuvvetin seçtiğimiz bölge boyunca negatif iken pozitif veya pozitif iken negatif değer almamasıdır. Bir başka deyişle kuvvet, bölgelerimiz boyunca sadece ya negatif ya da pozitif değerler olarak kalacak şekilde seçilmelidir. Bu durumda örneğimiz için 0-2 m aralığı I. bölge, 2-6 m aralığı II. bölge ve 6-8 m aralığı da III. bölge olarak belirlenebilir. Bu bölgelerin her birinin kuvvet eğrisi altında kalan alan bize işi verecektir. Toplam iş ise bu bölgeler için hesaplanan işlerin toplamıdır.

Enerji

İş yapabilme yeteneğine enerji denir. Cisim üzerine yapılan iş cismin hareket enerjisi olarak da bilinen kinetik ve durgun enerji olarak da isimlendirilen potansiyel enerjisinin toplamı olan mekanik enerji değişimine eşittir. Hareket eden bir nesne, masa üzerindeki bir bardak, bardak içerisindeki su vb. gibi sistemlerin mevcut enerjisi varsa, iş yapabiliyor demektir. Cisim veya sistem iş yaparak enerjisini harcar ve bu enerji başka enerji şekillerine (ısı, ışık, mekanik, kimyasal, elektrik ve nükleer enerji vb.) dönüşebilir. Bu nedenle iş ve enerji birimleri aynıdır (joule veya erg.). Enerji de iş gibi skaler bir büyüklüktür.

Kinetik Enerji (Hareket Enerjisi)

Kinetik enerji, cismin hızından ötürü sahip olduğu enerjidir. Kinetik enerji cismin sahip olduğu hızın doğrultusundan bağımsız olarak her zaman pozitif değer alır. Kütlesi m ve hızının büyüklüğü v olan bir cismin kinetik enerjisinin eşitliği aşağıdadır:

Kitabınızın 66. sayfasında yer alan Şekil 3.8’deki gibi yatay bir düzlemde bulunan m kütleli bir cisim sabit ivmesi ile hareket etsini. Cisim A noktasından geçerken 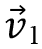hızına, B noktasından geçerken ise 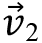hızına sahip olsun. Bu durumda cisim üzerine yapılan iş için elde edilen eşitlik aşağıdadır.

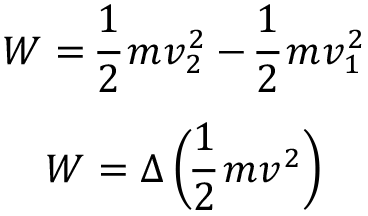
Bu ifadede parantez içindeki terim kinetik enerjidir ve W = ? E _K eşitliğiyle yazılır. Bu eşitlik iş-enerji teoremi olarak bilinir ve cisim üzerinde yapılan işin kinetik enerjisindeki değişim miktarına eşit olduğunu veya bir cismin kinetik enerjisi değişirse cismin üzerinde iş yapılmış olması gerektiğini ifade eder.

Kinetik enerji değişimi bulunurken ara hız değişimleri göz ardı edilip sadece son ve ilk hız değerlerinin alındığına dikkat ediniz. Hızın artma veya azalma biçimi de kinetik enerjiyi değiştirmeyecektir. Yukarıda yer alan kinetik enerji eşitliğinin negatif değer alması cismin hızının azaldığını gösterir ve enerji kaybettiğine işaret eder. Eşitliğin pozitif değer alması ise cismin hızının arttığını veya cismin enerji kazandığını gösterir.

Birden fazla parçacıktan oluşan sistemlerde (birden farklı cismin olduğu durumlarda) sistemin toplam kinetik enerjisi sistemi oluşturan her parçacığının kinetik enerjileri toplamıdır.

Potansiyel Enerji

Potansiyel enerjiyi her an iş yapabilme yetkinliği olarak tarif edebiliriz. Cismin bulunduğu konumun veya bağlı bulunduğu düzeneğin bir sonucu olarak ortaya çıkar. Potansiyel enerji, cismin bulunduğu ortamdaki kuvvetlere karşı yapılan iş olarak ta tarif edilir. Yerçekiminin olduğu bir ortamda, çekim kuvvetinin cisim üzerinde yaptığı iş, potansiyel enerji olarak tanımlanır.

Kitabınızın 69. sayfasında yer alan Şekil 3.11’i inceleyiniz. Şekilde biri asansörler diğeri merdivenle top taşıyan iki kişi görülmektedir. Topun kütlesini m olarak alırsak ağırlığı mg şiddetine sahip olacak ve yönü tüm hareket boyunca aşağıya doğru olacaktır. İkinci katta bulunan evin yerden yüksekliği de h olarak verilsin. Asansörle de çıkılsa merdivenle de çıkılsa toplar, yer çekimi kuvveti vektörünün tersi yönünde aynı yüksekliğe (h) çıkarılmıştır. Merdivenlerdeki dönüşlerde fazladan gidilen yatay yollar yer çekimi kuvveti vektörü ile 90° açı yaptığından iş yapılmaz, kabul edilir. Bu durumda topa etkiyen yer çekimine karşı yapılan iş; W = mgh olarak verilir. Bu enerji m kütleli top üzerinde depolanmıştır ve top bu enerji ile iş yapma yeteneğine sahiptir. Cismin yüksekliğinden dolayı kazandığı bu enerjiye potansiyel enerji denir.

Esneklik Potansiyel Enerjisi

Esnek cisimlerin, gergin veya sıkışık konumdayken sahip olduğu enerji esneklik potansiyel enerjisi olarak adlandırılır. Esneklik potansiyel enerjisi, esnek cisimleri denge konumundan uzaklaştırmak için yapılan işe eşittir. Kitabınızın 70. sayfasında yer alan Şekil 3.12’deki gibi bir yaya 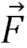kuvveti uygulanıp yayın gerilmesi buna bir örnektir.

Sürtünmesiz bir yüzeyde, bir yayın bir ucunu duvarda sabit bir A noktasına, diğer ucunu da m kütleli bir cisme bağlayalım (Sf. 70, Şekil 3.13). Cismi çekerek yayı x kadar gerelim (yayın uzamamış durumdaki konumunu sıfır aldık). Bu durumda yay tekrar eski konumuna gelmeye çalışır ve yayda F kuvveti oluşur. Bu kuvvete geri çağırıcı kuvvet denir.

Enerjinin Korunumu

Enerji ne yoktan var edilebilir ne de varken yok edilebilir fakat bir formdan başka bir forma dönüşebilir. Bu dönüşüm sırasında toplam enerji daima aynı kalır, değişmez. Bir kinetik enerji potansiyel enerjiye ya da sürtünme kuvvetlerinin harcadığı işe kullanılabilir. Belirli bir hızla giden aracın frene basıp durması sırasında aracın hızından dolayı sahip olduğu kinetik enerji, sürtünme kuvvetlerinin harcadığı işe dönüşmüştür. Yukarıda sözü geçen top örneğinden yola çıkarak bu durumu açıklayalım. Elimizdeki topu pencereden aşağıya doğru bırakalım. Bu durumda pencereden bıraktığımız anda ilk hızı sıfır olan topumuz herhangi bir düşüşte dahi belirli bir hıza kavuşacaktır. Bu durumun tersi de mümkündür. Top düşey ilk hızla yerden yukarıya doğru fırlatılırsa yükseldikçe topun kinetik enerjisi azalırken potansiyel enerjisi artar.

Güç ve Verim

Bazı durumlarda yapılan işin ne kadar zamanda yapıldığı önem taşır. Bu nedenle güç kavramı ortaya atılmıştır. Güç, iş yapma hızı olarak tanımlanır. Yapılan iş W ve işin yapıldığı süre ? t ise güç; eşitliğiyle verilir. Örnekler için kitabınızın 74. sayfasını inceleyiniz.

Bir makinenin verimi, makineden alınan gücün makineye verilen güce oranı olarak tarif edilir. Verim ? simgesi ile gösterilir ve 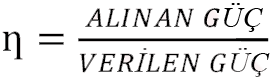eşitliğiyle verilir. Sürtünme, ses, ışık, deformasyon gibi enerji kayıpları nedeniyle alınan güç hiçbir zaman verilen güce eşit olamaz. Dolayısıyla verim her zaman 1’den küçük, sıfırdan büyüktür.

Momentum ve İtme

Bir cismin kütlesi ile hızının çizgisel momentum veya kısaca momentum olarak isimlendirilir. Momentum; 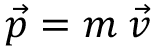eşitliğiyle gösterilir. Birimi kg.m/s’dir. Momentum vektörel bir niceliktir ve yönü cismin hızı yönündedir. Bu bakımdan cismin momentumunun bilinmesi cismin hangi yönde hareket ettiği bilgisini de verir.

İtme

Cisme etkiyen kuvvet ile kuvvetin etki süresinin çarpımına itme denir. Kuvvet vektörel büyüklük olduğundan itme de vektörel bir büyüklüktür. İtmenin birimi newtonsaniye’dir(N.s). Cisim üzerine etki süresi farklı olacak şekilde birden fazla kuvvet uygulandığında itme, her bir kuvvetin kendi etki süresiyle çarpımlarının vektörel toplamı olarak düşünülmelidir. Bir cisme etki eden itme, cismin momentumundaki değişime eşittir. Momentum değişimi, cismin son momentumuyla ilk momentumu arasındaki farktır.

Örn: Sürtünmesiz bir zeminde 4 m/s’lik sabit hızla kayan 10 kg kütleli bir top, duvara çarpıyor (Sf. 77, Şekil 3.18). Top duvarla 0,02 s’lik bir etkileşmeden sonra aynı hızla geri dönüyor. Cismin duvar üzerinde oluşturduğu ortalama kuvvet kaç N’dur?

Momentum değişimi hesaplanırken son momentumdan ilk momentumun farkı alınacağından cismin geliş ve dönüş yönleri önem taşır. Top duvara çarpıp döndükten sonra, hızının büyüklüğü aynı olmasına rağmen yönünün geliş hızına ters olacağına dikkat edelim. Bu durumda momentum değişimi, geliş momentumunun iki katı olacaktır. Sf. 76’daki Eş. 3.29 kullanılarak:

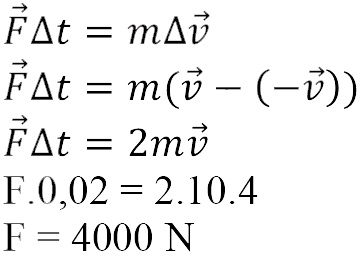
Momentum Korunumu

Cismin bir fiziksel olaydan önceki ve sonraki momentumlarının eşit olması momentum korunumu olarak isimlendirilir. Momentumun yönünü ve büyüklüğünü değiştirebilmek için hızın değişmesi dolayısıyla cisim üzerine etki eden dış kuvvetin yönü, büyüklüğü veya etki süresi niceliklerinden en az birinin değişmesi gereklidir. 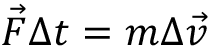eşitliğine göre itmenin yönü uygulanan net kuvvetin yönü olmakla birlikte aynı zamanda momentum değişimi yönündedir. Bir başka deyişle belirli bir doğrultuda momentum değişiminden bahsedebilmek için o yönde net bir dış kuvvet olması gerekir. Sf. 78’de yer alan örnek ve çözümü inceleyerek konuyu daha net anlayabilirsiniz.

Momentumun korunumu için türetilen eşitliklerin vektörel olduğuna dikkat edelim. Birden fazla bileşeni olan bir cisim için momentumun korunumundan bahsedebilmek için her hız bileşeni doğrultusunu ayrı ayrı ele almak gerekir. Eğer belirli bir doğrultuda dış kuvvet var ise dış kuvvetin yönü doğrultusunda momentum korunmaz iken diğer doğrultularda dış kuvvet olmadığı için o doğrultulardaki momentum korunur.

Çarpışmalar

Hareketli bir cismin, durmakta olan veya hareketli diğer bir cisimle etkileşmesine çarpışma denir. Çarpışmalar cisimlerin çarpışmadan önceki ve sonraki doğrultularına göre ikiye ayrılır. Eğer çarpışma öncesi ve sonrası cisimler aynı doğrultuda ise bu merkezi çarpışma, değilse merkezî olmayan çarpışma olarak isimlendirilir.

Çarpışmada çarpışmayı yapan cisimlerin hareketlerinde keskin bir değişme olur. Çarpışmaların şekli nasıl olursa olsun, dış kuvvetlerin olmadığı çarpışmalarda momentum korunur ve cisimlerin çarpışmadan önceki toplam momentumları çarpışmadan sonraki toplam momentumlarına eşittir. Dış kuvvetin olduğu çarpışma durumlarında ise momentum korunmaz.

Çarpışmaları enerji korunumuna göre esnek ve esnek olmayan çarpışma diye ikiye ayırabiliriz. Esnek çarpışma enerjinin değişmediği çarpışmalardır. Enerji skaler bir büyüklük olduğu için korunumundan bahsederken cisimlerin çarpışmadan önceki ve sonraki toplam enerjisinden bahsedilir. Momentum ise vektörel büyüklük olduğu için, her doğrultuyu ayrı ayrı ele alıp dış kuvvetin olmadığı doğrultuda momentumun kesinlikle korunduğunu söyleyebiliriz.

Esnek Çarpışma

Esnek çarpışmada momentumun yanı sıra, mekanik enerji de korunur. Çarpışma sırasında enerji kaybı yoktur. Bu tür çarpışmanın anlaşılması için bilardo toplarının çarpışmalarını örnek verebiliriz. Bu çarpışmalarda sürtünme ihmal edildiğinde dış kuvvet olarak sadece yer çekimi kuvveti vardır ve bu kuvvetin yönü topları çarpıştırdığımız masa düzlemine diktir; dolayısıyla topların hızlarına herhangi bir katkısı yoktur. Böylelikle momentum korunur. Enerji ise toplar çarpıştığı andaki deformasyon ihmal edilirse (yine dış kuvvet yok) korunur. Esnek çarpışma konusunu daha iyi anlayabilmek için Sf. 82’de yer alan soru örneklerini ve çözümleri inceleyiniz.

Esnek Olmayan Çarpışma

Esnek olmayan çarpışmada momentum korunsa da kinetik enerji korunmaz. Çarpışma sırasında kinetik enerjinin büyük kısmı ısıya dönüştüğünden enerji kaybı olur. Esnek olmayan çarpışma konusunu daha iyi anlayabilmek için Sf. 83 ve 84’te yer alan soru örneklerini ve çözümlerini inceleyiniz.