TIBBİ İSTATİSTİK - Ünite 3: Ortalamalar ve Değişkenlik Ölçüleri Özeti :

PAYLAŞ:

Ünite 3: Ortalamalar ve Değişkenlik Ölçüleri

Giriş

Frekans dağılımları ve grafikler, bir veri seti içindeki değerlerin dağılımı hakkında genel bir fikir vermede etkilidir. Bununla birlikte daha ileri analizler için, verilerin tek bir değerle ifade edilebileceği, kesin bilgilere ihtiyaç vardır. Bu amaçla ortalamalar kullanılmaktadır. Ayrıca verilerin bir değer etrafında nasıl dağıldıklarının ölçüsü olarak değişkenlik ölçülerinden yararlanılmaktadır.

Verilerin Özetlenmesi

Bir araştırma sonucu toplanan verilerin frekans serisi veya gruplandırılmış seri halinde gösterilmesi, veriler hakkında genel fikir verebilir. Yine bu verilerin grafikle gösterilmesi, verilerin nasıl dağıldıkları hakkında genel bir eğilim yansıtır. Ancak bunların hiçbiri verilerin tek bir değerle gösterilmesini sağlamazlar. Oysa derlenen verileri “tek bir sayıda” özetleyecek kolay ölçütlere de ihtiyaç vardır. Bu özet veri, araştırma sonunda derlenen verilerin hangi değer etrafında toplandıklarının bir göstergesi olacaktır. Bir seriyi temsil etmeye ve özetlemeye yarayan tek bir rakama ortalama denir. Dolayısıyla ortalamalar veri setindeki en küçük değerden daha küçük, en büyük değerden de daha büyük olamazlar.

Hesaplanan ortalamanın serideki terimlerin çoğuna yakın değer alması, söz konusu ortalamanın seriyi iyi temsil ettiğini gösterir. Ortalamalar hesaplanırken, serideki bütün gözlem değerleri hesaba katılarak hesaplanıyorsa buna duyarlı ortalamalar , bazı gözlem değerlerine göre hesaplanıyorsa buna da duyarlı olmayan ortalamalar adı verilir. Başka bir ifadeyle ortalama hesaplanırken, gözlem değerlerinden birinin değiştirilmesiyle ortalama değeri değişiyorsa bu duyarlı ortalamadır. Aksi durumda gözlem değerlerinden birinin değiştirilmesi ortalama değerini etkilemiyorsa buna da duyarlı olmayan ortalama denir. Duyarlı ortalamalara aritmetik ortalama ve geometrik ortalama, duyarlı olmayan ortalamalara ise mod ve medyan örnek verilebilir.

Aritmetik Ortalama

İstatistikte en çok kullanılan ve ortalama denilince akla gelen ilk ortalama aritmetik ortalamadır. Aritmetik ortalama , veriler toplamının veri sayısına bölünmesi şeklinde tanımlanabilir.

Bir ortalama, ana kütlenin tamamı için hesaplanacağı gibi, ana kütleden seçilen bir örneklem kütlesi için de hesaplanır. Kütledeki birimlerin sayısı, yani kütle büyüklüğü genellikle N ve kütle ortalaması da µ ile gösterilir. X değişkeninin ortalaması; ? toplam simgesi, X _i ilgili değişkenin gözlemlerinin (i=1,…,N) aldığı değerler olmak üzere aşağıdaki eşitlik yardımıyla hesaplanmaktadır:

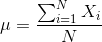
$\mu =\frac{\sum _{i=1}^{N}X_{i}}{N}$

Ancak kütle çok büyük olduğunda, bunun tamamını gözlemlemek daha çok maliyet ve zaman gerektirir ya da bazen kütlenin tamamı incelemek imkânsız olabilir. Böyle durumlarda daha az sayıda birimle araştırma yapabilmek amacıyla örneklemeye başvurulur. Kütle içinden seçilen birim sayısı da genellikle n simgesiyle gösterilir. n birim için hesaplanan ortalamaya örneklem ortalaması denir ve aşağıdaki gibi hesaplanır:

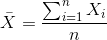
$\bar{X}=\frac{\sum _{i=1}^{n}X_{i}}{n}$

Eğer istatistik serisi, frekans serisi veya gruplandırılmış seri ise aritmetik ortalama şu eşitlik yardımıyla hesaplanmaktadır:

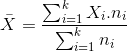
$\bar{X}=\frac{\sum _{i=1}^{k}X_{i}.n_{i}}{\sum _{i=1}^{k}n_{i}}$

Ancak belirtmek gerekir ki, gruplandırılmış serilerde aritmetik ortalama hesaplanırken, her bir grubun ortalaması alındığından, gruplandırılmış serilerdeki aritmetik ortalama yaklaşık olarak hesaplanabilmektedir.

Aritmetik ortalama, aşırı küçük veya büyük değerlerden etkilenen bir ortalamadır. Dolayısıyla veriler içinde, diğer verilere nazaran aşırı küçük veya büyük değerler olması durumunda, aritmetik ortalama tüm verileri temsil eden bir ortalama olmayacaktır. Böyle durumlarda ise temsili olabilecek yani, verilerin geneline yakın olabilecek ortalama geometrik ortalamadır.

Geometrik Ortalama

Bir istatistik serisindeki veriler geometrik olarak artıyorsa ya da diğer verilere nazaran aşırı büyük ya da küçük değerler varsa, bu durumda aritmetik ortalama temsili olmayacağından, geometrik ortalama hesaplanır. Mikroorganizmaların çoğalması, nüfus artışı, gibi birbirinin katları olarak çoğalan yani geometrik artış gösteren verilerde geometrik ortalama kullanılır. Diziler için geometrik ortalama aşağıdaki gibi hesaplanır:

$G.O.=\sqrt[n]{x_{1.}x_{2}...x_{n}}$

Ancak veri sayısı çok olduğunda bu şekilde hesaplamak zorlaşacağından, önce x _i ’lerin her birinin e tabanına göre doğal logaritması olan “ln” leri alınır, daha sonra bunların toplamı terim sayısına bölünür. En sonunda bulunan bu sayının exponansiyeli alınır ve aşağıdaki gibi hesaplanır:

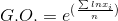
$G.O.=e^{ (\frac{\sum lnx_{i}}{n} )}$

Geometrik ortalama, gruplandırılmış ve frekans serilerinde ise aşağıdaki formülle belirlenir:

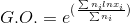
$G.O.=e ^{(\frac{\sum n_{i}lnx_{i}}{\sum n_{i}})}$

Tartılı Aritmetik Ortalama

Ortalamaların ve oranların ortalamaları hesaplanmak istendiğinde ya da farklı zaman ve yerde yapılan deney sonuçlarını birleştirerek ortak bir değer hesaplama gerektiğinde, tartılı aritmetik ortalama hesaplanır. n _i ’ler tartı olmak üzere, ortalamaların ortalaması aşağıdaki eşitlik yardımıyla hesaplanmaktadır:

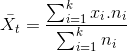
$\bar{X_{t}}=\frac{\sum _{i=1}^{k}x_{i}.n_{i}}{\sum _{i=1}^{k}n_{i}}$

Oranların ortalaması hesaplanırken, p _i oranları göstermek üzere şu eşitlikten yararlanılır:

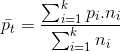
$\bar{p_{t}}=\frac{\sum _{i=1}^{k}p_{i}.n_{i}}{\sum _{i=1}^{k}n_{i}}$

Mod

İstatistikte, diziler ve frekans serileri için hesaplanması en kolay ortalama mod değeridir. Bir dizide en çok tekrarlanan değere mod değeri denir. Frekans serilerinde bu değer en yüksek frekansa sahip olan değer olacaktır.

Gruplandırılmış serilerde mod değeri hesaplanırken L _a ; mod grubunun alt değeri, ? ₁ ; mod grubunun frekansı ile bir önceki grubun frekansı arasındaki fark, ? ₂ ; mod grubunun frekansı ile bir sonraki grubun frekansı arasındaki fark, c _m ; mod grubunun aralığı olmak üzere aşağıdaki eşitlikten yararlanılmaktadır:

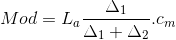
$Mod=L_{a}\frac{\Delta _{1}}{\Delta _{1}+\Delta _{2}}.c_{m}$

Gruplandırılmış serilerde frekans değeri en yüksek olan grup mod grubu olarak tanımlanır. Eğer grup aralıkları farklı ise grup aralıklarının ayarlanması gereklidir.

Medyan

Küçükten büyüğe sıralanmış verileri, iki eşit kısma ayıran ve tam ortaya düşen değere medyan (ortanca değer) adı verilir. Dizilerde medyan hesabı oldukça kolaydır. Önce gözlem sayısı 2’ye bölünür (n/2). Eğer (n/2) bir tamsayı değilse, bu değer tamsayıya çevrilir. Aranan medyan değeri de tam ortaya düşen bu gözlem değeridir. Eğer (n/2) tamsayı ise aranılan medyan değeri aşağıdaki gibi belirlenir:

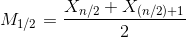
$M_{1/2}=\frac{X_{n/2}+X_{(n/2)+1}}{2}$

Frekans serilerinde medyan değerini hesaplayabilmek için frekans serisindeki gözlem değerlerinin sırasının bilinmesi gerekir. Bu nedenle küçükten büyüğe “birikimli frekanslar” oluşturulur ve medyan değeri dizilerdeki gibi hesaplanır. Gruplandırılmış serilerde medyan hesabı ise aşağıdaki formülle hesaplanacaktır:

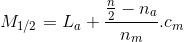
$M_{1/2}=L_{a}+\frac{\frac{n}{2}-n_{a}}{n_{m}}.c_{m}$

Formülde L _a ; medyan grubunun alt değeri, n _a ; medyan grubundan önceki frekansların toplamı, n _m ; grup frekansı ve c _m ; medyan grubunun aralığını temsil etmektedir.

Değişkenlik Ölçüleri

Ortalamalar, serileri özetlemek için gerekli olsa da gözlem değerlerinin birbirine yakınlık derecesini belirlemediğinden yeterli değildir. Ortalamaları aynı olan seriler birbirinden çok farklı olabilir. Dolayısıyla bir istatistik serisi incelenirken gözlem değerlerinin ortalaması yanında, ortalama etrafındaki dağılımlarına da ihtiyaç vardır. Bir istatistik serisini oluşturan gözlem değerlerinin birbirlerinden ya da ortalamadan uzaklıkları, verilerin nasıl değişim gösterdiğini belirtir. Bunları hesaplamaya yarayan ölçülere de “değişkenlik ölçüleri” denir. En sık kullanılan değişkenlik ölçüleri standart sapma ve değişim katsayısıdır.

Standart Sapma

İstatistikte en sık kullanılan değişkenlik ölçüsü standart sapmadır. Standart sapma ve karesi olan varyans pek çok istatistiksel analize temel oluşturur. Dizilerde ana kütle standart sapması; µ ana kütle ortalaması, x _i incelenen değişkenin ilgili gözlem değeri olmak üzere şu eşitlikle hesaplanmaktadır:

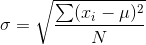
$\sigma =\sqrt{\frac{\sum (x_{i}-\mu )^{2}}{N}}$

Bunun karesi olan ? ² ise “ana kütle varyansı” olarak ifade edilir. Örneklem standart sapması ise s ile ifade edilir ve aşağıdaki gibi belirlenir:

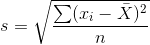
$s=\sqrt{\frac{\sum (x_{i}-\bar{X})^{2}}{n}}$

Bunun karesi olan s ² değerine ise “örneklem varyansı” denir. Frekans serilerinde ve gruplandırılmış serilerde örneklem standart sapması aşağıdaki eşitlikten yararlanılarak hesaplanır:

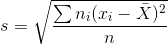
$s=\sqrt{\frac{\sum n_{i}(x_{i}-\bar{X})^{2}}{n}}$

Mutlak bir ölçü olan standart sapma, gözlem değerlerinin büyüklüğünden etkilenen bir ölçüdür. Ayrıca ölçü birimleri farklı olan serilerin karşılaştırılmasında da standart sapma kullanılamaz. Dolayısıyla ölçü birimleri (cm, lt, hg v.b), ve terimlerin değeri farklı olan serilerin karşılaştırılmasında değişim katsayısı kullanılır.

Değişim Katsayısı

Standart sapmanın, aritmetik ortalamaya bölünmesiyle elde edilen değişim katsayısı, oransal bir ölçüdür. Dolayısıyla değişim katsayısı terimlerin büyüklüğünden ve ölçü birimlerinden etkilenmez. Değişim katsayısı aşağıdaki formülle hesaplanır:

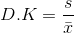
$D.K=\frac{s}{\bar{x}}$

Mutlak bir ölçü olan standart sapmanın aksine, değişim katsayısının ölçü birimi yoktur. Çünkü formülün pay ve paydasında yer alan ve aynı ölçü birimine sahip olan standart sapma ve aritmetik ortalama birbirine bölündüğü için, sonuçta ölçü birimine sahip olmayan bir oran kalır. Tek bir serinin değişkenliğini belirlemek için çok kullanışlı olmayan değişim katsayısı, daha çok iki ve daha fazla serinin karşılaştırılması için kullanılır. Değişim katsayısı küçük olan serilerin, diğerlerine göre daha az değişken olduğu ifade edilecektir. Bunun anlamı ise değişim katsayısı küçük olan serinin daha homojen yani birbirine daha yakın terimlerden oluştuğudur.