Ünite 5: İlişki Kuralları

İlişki Kuralları

Büyük veri kümeleri içerisinde belirli veriler arasındaki ilişkileri bulan ve olayların birlikte gerçekleşme ihtimallerini geçmiş verileri analiz edip ortaya koyarak geleceğe yönelik çalışmaları destekleyen veri madenciliği yöntemine ilişki kuralları denilmektedir.

Genel olarak ilişki kuralları sayesinde büyük miktarlardaki veriler arasından ilginç birliktelik örüntüleri keşfedilerek karar verme, pazarlama ve iş yönetimi vb. gibi konularda birçok fayda sağlanmaktadır. İlişki kuralları; ekonomi, eğitim, e-ticaret, pazarlama, iletişim ve sağlık gibi birçok sektörde geniş kullanıma sahip veri madenciliğinin özel bir uygulama alanıdır. İlişki kurallarının kullanım amaçlarına örnek verilecek olursa, Sigorta sektöründe alışılmışın dışında gelen sigorta talepleri bir dolandırıcılık girişiminin belirtisi olabilir. Dolayısıyla tedbir ve önlem almak amacıyla kullanılabilir.

İlişki kuralları, günlük hayatta özellikle insanların beklentilerinin belirlenmesinde çoğu zaman başarısız olmaktadır. Örneğin, bireysel bankacılık alanında çapraz satış modellerinin belirlenmesinde ilişki kuralları iyi bir seçim değildir. Çünkü oluşturulan kurallar genellikle halihazırda uygulanan promosyon stratejileriyle birebir aynı çıkmaktadır. Bunun altında yatan neden ise zaten her müşteriye başlangıçta standart bir ürün hizmet paketinin sunulmasıdır. Farklılaşma ancak müşterilerin zaman içerisinde ilave ürün ve hizmet taleplerinin olması halinde gözlemlenebilir.

Pazar sepeti analizi , müşterilerin alışveriş alışkanlıklarının veritabanındaki bilgiler aracılığı ile ortaya çıkartılması işlemidir. Pazar sepeti analizinde nesneler, müşteriler tarafından satın alınan ürünlerdir. Bir kalemde satın alınan ve içerisinde birçok nesneyi barındıran satın alma ise işlem veya kayıt olarak nitelendirilir. Dolayısıyla Pazar sepeti analizinde, bir işlemde alınan nesneler arasındaki ilişkiler incelenerek çeşitli ilişki kuralları oluşturulur. Oluşturulan bu kurallar aracılığı ile müşterilerin daha sonra yapacakları alışverişlerinde hangi mal ve hizmeti alma eğiliminde oldukları saptanarak daha fazla ürün satışı gerçekleştirebilmek için gerekli düzenlemeler yapılabilir.

Büyük veri kümeleri içerisinde nesneler arasında ilişki bulmak için algoritma geliştirmek çok zor olmamasına karşın, buradaki asıl zorluk geliştirilen algoritma ile elde edilecek önemli ve önemsiz çok sayıda kural içerisinden işe yarayacak bilgiyi üreten ilişki kurallarının seçilmesidir. Ortaya çıkarılan ilişki kuralları içerisinden önemli veya ilginç olanları ayırt edebilmek için birtakım ölçütlere ihtiyaç duyulur. Bunun için temel olarak kullanılan ölçütler destek ve güven ölçütleridir . İlişki analizinin amacı, elde edilecek birçok kural içerisinden belirlenen destek ve güven eşik değerlerini sağlayan kuralların seçilmesidir.

Pazar Sepeti Analizi

Pazar sepeti analizi, müşterilerin daha önceden yapmış oldukları alışverişlerinden oluşan veritabanından her bir alışverişinde birlikte almış olduğu ürünler arasındaki ilişkilerden yola çıkılarak müşterilerin alışveriş alışkanlıklarının belirlenmesidir . Pazar sepeti analizinde müşterilerin alışverişlerinde aldıkları her bir ürün nesne, içerisinde birçok nesneyi yani ürünü barındıran her bir alışveriş ise işlem olarak ifade edilir. Dolayısıyla ilişki kurallarını matematiksel bir model olarak ifade edebilmek için,

I = {i ₁ , i ₂ , ... , i _m } nesneler (ürünler) kümesi

D ={t ₁ , t ₂ , ... , t _n } işlemler (alışverişler) veritabanı

olarak tanımlansın. Yapılan tanımlamalara göre t _i ? I’dır. Yani her bir işlem ya da alışverişi ifade eden t _i , I nesneler kümesinin bir alt kümesidir. Veritabanında yer alan her bir alışveriş (t _i ) ayrı bir numara ile ifade edilir ki bu numaralara Tid denir. Dolayısıyla D, işlemlerden oluşan veri kümesini yani tüm alışverişlerden oluşan veritabanını ifade eder .

İlişki Kuralı: A ve B iki nesne seti olsun. Belirlenen destek eşik değeri s ve belirlenen güven eşik değeri c için A ? B şeklinde ifade edilen bir kural,

1. A nesne setinin destek değeri Destek (A) ? s
2. A ? B kuralının güven değeri Güven (A ? B) ? c

koşullarını sağlıyor ise A ? B kuralı bir ilişki kuralı olarak adlandırılır. Burada A öncül , B ise sonuç olarak adlandırılır ki A ? I, B ? I ve A ? B= Ø ’dir. Yani A ve B nesne setleri, I nesneler kümesinin elemanlarından oluşan nesne setleridir ve bu nesne setlerinin ortak elemanları yoktur .

Özellikle pazarlama alanında satışları arttırabilmek amacıyla yapılan birçok çalışma bulunmaktadır. Örneğin bir marketten yapılan alışverişler üzerinden sıklıkla birlikte alınan ürünleri belirleyebilmek için A ? B şeklinde bir ilişki kuralı oluşturulabilir. Marketten süt ve ekmek alan müşterilerin bunlarla birlikte çoğunlukla yumurta da aldıkları yönünde oluşturulacak bir ilişki kuralı {Süt, Ekmek} ? {Yumurta} şeklinde ifade edilir. Böyle bir ilişkiyi keşfeden market sahibi, süt ve ekmek alacak müşterilere yumurta fiyatında indirim yaparak veya satış reyonunda süt ve ekmeğin yanına yumurta da koymak suretiyle satışlarını arttırmayı deneyebilir.

İncelenecek nesneler kümesinin sahip olduğu nesne sayısına göre oluşturulabilecek ilişki kuralı sayısı da değişmektedir. İlişki kuralı elde etmek için ilk olarak kural oluşturmada kullanılacak nesne kümesi sayısının bilinmesi gerekir. m adet nesne içeren bir I nesneler kümesinden elemanları birbirinden farklı oluşturulması mümkün tüm nesne setlerinin sayısı 2 ^m tanedir. Ancak bu nesne setlerinden bir tanesi boş kümedir ve boş küme ilişki kuralı belirlemek amacıyla kullanılamayacağından, ilişki kuralı belirlemede kullanılacak nesne seti sayısı 2 ^m -1 tane olur

Örneğin m=4 adet nesne içeren bir I={a, b, c, d} nesneler kümesinden farklı nesne sayılarına sahip, oluşturulması mümkün tüm nesne setlerinin sayısı; 2 ^m = 2 ⁴ =16 tane olur. Bu 16 nesne seti içerisinde var olan boş küme, ilişki kuralı oluşturmak amacı ile kullanılamaz. Dolayısıyla ilişki kuralı oluşturmak için kullanılabilecek toplam nesne seti sayısı 2 ^m -1=2 ⁴ -1=16-1=15 tanedir.

İkinci olarak, kural belirlemede kullanılabilecek nesne setleri içerisinden kaç tanesinin k tane nesne içeren nesne seti olduğunun bilinmesi gereklidir. m adet nesne içeren bir I nesneler kümesinden ilişki kuralı oluşturmada kullanılabilecek k (1 ? k ? m) tane nesne içeren nesne kümelerin sayısı 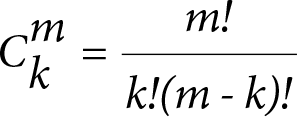adet olacaktır.

Son olarak, oluşturulabilecek toplam ilişki kuralı sayısının bilinmesi gerekir. m adet nesne içeren bir I nesneler kümesinden toplamda 3 ^m -2 ^m+1 +1 adet ilişki kuralı oluşturulabilir. Örneğin, m=5 nesne içeren nesneler kümesinden 3 ⁵ -2 ⁵⁺¹ +1=180 tane ilişki kuralı oluşturulabilirken, m=10 nesne içeren nesneler kümesinden 3 ¹⁰ -2 ¹⁰⁺¹ +1=57.002 tane ilişki kuralı oluşturulabilir.

Bir ilişki kuralının gücü , o kural için hesaplanacak destek ve güven değerleri ile ölçümlenebilir.

İlginç Kural Belirleme Ölçütleri (Rule Interestingness Measures)

İlgilenilen problemde ilişki kurallarını belirlemede kullanılacak nesneler kümesinin eleman sayısı arttıkça bu nesneler aracılığı ile oluşturulacak kural sayısı da katlanarak artmaktadır. Bu kurallar içerisinden belirli ölçütler kullanmak suretiyle bilgi üretmek amacıyla kullanılmayacak, önemsiz kuralların elenmesi gerekir. Bir alışveriş veritabanından oluşturulacak ilişki kuralları arasından işe yarayacak bilgiyi üretmek amacıyla kullanılacak ilişki kuralı ilginç kural olarak tanımlanabilir. Bir ilişki kuralının ilginç kural olarak değerlendirilebilmesi için,

1. Daha önceden keşfedilmemiş,
2. Eyleme dönük, bir başka ifadeyle uygulanabilir olması gerekir.

Bir ilişki kuralının “ilginç”liği, kişiden kişiye değişiklik gösterebilen yani subjektif bir karar olmasına rağmen, bu kararın verilebilmesi için verilerden elde edilebilecek ilişki kurallarının bilimsel veya objektif ölçütler aracılığı ile de elenmesi beklenir. İlginç kuralların belirlenebilmesi amacıyla kullanılan başlıca objektif ölçütler destek ve güven ölçütleridir.

Destek (Support)

İlginç olarak nitelendirilen ve bilgi üretmek amacıyla kullanılacak bir ilişki kuralının belirlenebilmesi için kullanılan ilk ölçüt, nesne setleri içerisinden eleme yapılmasını sağlayan destek değeridir. Karar verici tarafından belirlenmiş olan destek eşik değerine eşit veya bu değerin üzerinde destek değerine sahip nesne setleri üzerinden işlemler yürütülürken, bu değerin altında destek değerine sahip nesne setleri elenerek değerlendirme dışı bırakılır. Bir A nesne setinin destek değeri, D işlemler veritabanında A nesne setini içeren işlem sayısının veritabanındaki tüm işlemlerin sayısına oranı şeklinde elde edilir ve 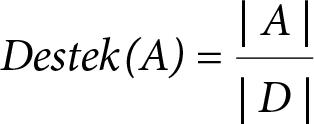eşitliği yardımıyla hesaplanır.

Eşitlikte |A|, tüm işlemler içerisinde A nesne setini içeren işlem sayısını, |D| ise işlemler veritabanındaki tüm işlemlerin sayısını ifade eder. Bir A nesne setinin destek değeri, Bir A nesne setinin destek değeri, P(A), A nesne setinin gözlenme olasılığıdır. Destek değeri [0,1] aralığında değer alır ve yüzde olarak yorumlanır.

Örneğin , beş İşlemden Oluşan Market Veritabanı

Tid   Nesneler

1. Süt, Ekmek
2. Ekmek, Yumurta
3. Ekmek, Şeker
4. Süt, Ekmek, Yumurta
5. Ekmek, Yumurta

Veritabanı için iki nesne içeren bir A= {Süt, Ekmek} nesne setinin destek değeri;

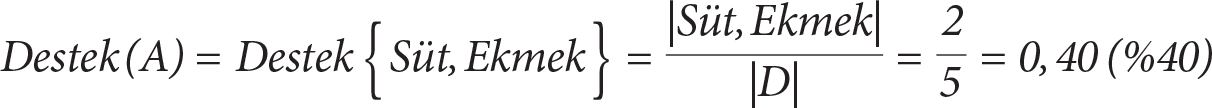
(%40) olarak elde edilir. Veritabanında yer alan toplam 5 işlemin 2 tanesinde (1. ve 4. işlemlerde) süt ve ekmek nesneleri birlikte alınmış olduğundan, elde edilen bu destek değeri alışverişlerin %40’ında süt ve ekmeğin birlikte alınmış olduğunu ifade eder.

Konu ile ilgili örnek S.108’de incelenebilir .

A ? B şeklindeki bir ilişki kuralının destek değeri, aslında P(A ? B)’dir. Yani A ve B nesne setlerinin birlikte gözlenme olasılığıdır.

Bir ilişki kuralının destek değeri, D işlemler veritabanında A ve B nesne setlerini birlikte içeren işlem sayısının veritabanındaki tüm işlemlerin sayısına oranı şeklinde elde edilir ve 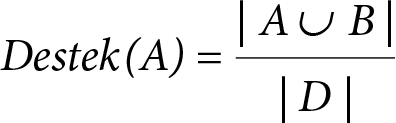eşitliği ile hesaplanır.

Örneğin, verilen veritabanı üzerinden belirlenecek {Süt, Ekmek} ? {Yumurta}şeklindeki bir ilişki kuralının destek değeri;

olarak elde edilir. Hesaplanan bu destek ! değeri, yapılan alışverişlerin %20’sinde süt, ekmek ve yumurtanın birlikte alınmış olduğunu ifade eder.

Destek Eşik Değeri: İlginç kural elde edebilmek için ilk eleme işlemi, hesaplanan destek değerleri üzerinden yapılır. Bu elemeyi yapabilmek için ise önceden bir destek eşik değerinin belirlenmiş olması gerekmektedir. Belirlenecek destek eşik değeri, tüm nesne setleri içerisinden bu destek eşik değerinden daha küçük destek değerine sahip nesne setlerinin elenmesini sağlar. Örneğin, beş işlemden oluşan market veritabanı verileri için destek eşik değerinin 0,30 olarak belirlenmiş olduğunu varsayalım. Bu durumda, bir nesne içeren nesne setleri içerisinden sadece {Şeker} nesne setinin destek değeri 0,20 olduğu için ve destek eşik değerinden küçük olduğu için elenir. Benzer şekilde iki nesneden oluşan nesne setleri arasından ise {Süt, Şeker}, {Ekmek, Şeker}, {Süt, Yumurta} ve {Yumurta, Şeker} nesne setlerinin hesaplanan destek değerleri belirlenmiş olan 0,30 destek eşik değerinden daha küçük oldukları için elenerek değerlendirme dışı bırakılırlar. Son olarak üç ve dört nesneden oluşan nesne setleri içerisinden ise hiçbir nesne setinin bu destek eşik değerini aşamadığı görülür. Dolayısıyla tüm üç ve dört nesne içeren nesne setleri de elenmiş olur. Elenen bu nesne setleri ilişki kuralı oluşturmak için kullanılmazlar.

Belirlenecek destek eşik değerinin çok yüksek bir değer olması, ilginç kural elde edebilmek için ele alınacak nesne setlerinin sayısını aşırı derecede azaltacaktır. Aksine destek eşik değerinin çok küçük bir değer olarak belirlenmesi durumunda ise, aşırı fazla nesne setinin değerlendirilmesi gerekliliği durumu ile karşı karşıya kalınacaktır. Özellikle büyük veri tabanlarında düşük destek eşik değeri belirlenerek elde edilecek birçok ilişki kuralı, karar verecek kişi için ilginç olma niteliği taşımamakta ve bilgi üretmek amacıyla kullanılamamaktadır. Bu durum, ilişki kurallarının belirlenmesinde yaşanan en büyük sorunlardan birisidir.

Belirlenen destek eşik değerine eşit veya daha büyük destek değerine sahip nesne setine sık görülen nesne seti denir.

Güven (Confidence)

İlginç ilişki kuralı elde edebilmek için kullanılan ikinci ölçüt, güven değeridir. Öncelikle karar verici tarafından belirlenmiş olan destek eşik değerine eşit ya da daha büyük destek değerine sahip nesne setleri yani sık görülen nesne setleri ile oluşturulması mümkün tüm ilişki kuralları oluşturulur. Karar verici tarafından belirlenmiş olan güven eşik değerine eşit ya da daha büyük güven değerine sahip ilişki kuralları ilginç kural elde etmek için değerlendirilmeye alınırken, bu değerin altında güven değerine sahip ilişki kuralları ise elenir, değerlendirilmez.

eşitliği ile hesaplanır. A ? B şeklindeki bir ilişki kuralının güven değeri, aslında A’yı içeren işlemlerin aynı zamanda B’yi de içerme olasılığıdır yani P(B-A)koşullu olasılığıdır. Yani A bilindiğinde B’nin ortaya çıkma olasılığıdır.

Konu ile ilgili örnek S.110’da incelenebilir.

Güven Eşik Değeri : İlginç kural belirlemede ikinci eleme işlemi, sık görülen nesne setleri üzerinden belirlenecek ilişki kuralları için hesaplanan güven değerleri ile yapılır. Belirlenecek güven eşik değerinin eleme gücü yüksek olmalı yani olabildiğince büyük seçilmelidir. Genellikle oluşturulan kuralın güçlü destek ve yüksek güven oranına sahip olması istenir. Belirlenen destek ve güven eşik değerleri üzerinde destek ve güven değerine sahip ilişki kuralına güçlü kural denir. İlişki analizinin temel amacı, bu şekilde tanımlanan güçlü kuralları tespit etmektir.

Kaldıraç (Lift)

İlişki kuralı oluşturmak için kullanılan algoritmalarının hepsi ilişki kuralı oluşturmada destek ve güven eşik değerlerini kullanır. Bazı durumlarda değerlendirilmesi gereken güçlü kural sayısı yine de fazla olabilmektedir. Ortaya çıkan güçlü kurallar içerisinden bir seçim yapabilmek ve problemin amacına en uygun ilişki kuralını belirleyebilmek için ilave kısıtlamalar kullanmak gerekmektedir. Bunlar içerisinden en çok kullanılan ölçüt ise, öncül(A) ve sonuç(B) nesne setleri arasındaki ilişkinin(korelasyonun) belirlenmesi temeline dayanarak hesaplanan kaldıraç(lift) değeridir.

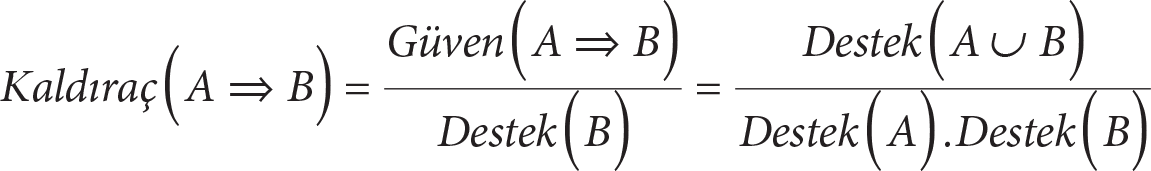
Eşitliği ile hesaplanır. Oluşturulan güçlü ilişki kuralının ilginç yani bilgi üretmede kullanılabilir bir kural olup olmadığının bir ölçüsü olarak hesaplanan kaldıraç değeri [0,?) arasında değer alır ve yüzde olarak ifade edilir. Hesaplanan kaldıraç değerinin,

• Kaldıraç (A ? B)<1 olması A ve B nesne setleri arasında ters yönlü (negatif) bir ilişki olduğunu,
• Kaldıraç (A ? B)=1 olması, A ve B nesne setleri arasında ilişki olmadığını
• Kaldıraç (A ? B)>1 olması, A ve B nesne setleri arasında aynı yönlü (pozitif) bir ilişki olduğunu ifade eder.

A ? B şeklindeki bir ilişki kuralının kaldıraç değeri, aslında A ve B nesne setlerinin birlikte gözlenme olasılığının A’nın ve B’nin ayrı ayrı gözlenme olasılıklarının çarpımına oranıdır yani 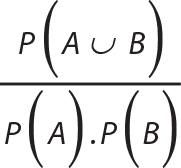‘dir. dir.

Konu ile ilgili örnek S.112’de incelenebilir.

İlişki Kuralı Belirleme Aşamaları

Genel olarak, bir ilişki kuralı oluşturmak iki temel adımdan oluşan bir süreçtir.

1. Adım : Sık Görülen Nesne Setlerinin Elde Edilmesi: Karar verici tarafından belirlenen destek eşik değerine eşit ya da daha yüksek destek değerine sahip nesne setleri yani sık görülen nesne setleri elde edilir.
2. Adım: Sık Görülen Nesne Setleri ile Güçlü İlişki Kuralının Elde Edilmesi : Birinci adımda belirlenen en yüksek mertebeye sahip yani en fazla nesne içeren sık görülen nesne setinin elemanları kullanılarak ilişki kuralları oluşturulur. k adet nesne içeren bir sık görülen nesne seti L _k şeklinde gösterilir. L _k ’nın elemanları kullanılarak oluşturulacak toplam ilişki kuralı sayısı 2 ^k -2 tanedir.

Etkin bir şekilde bir ilişki kuralı oluşturabilmek için zaman içerisinde AIS, SETM, Apriori, Eclat ve FP-Growth gibi birçok algoritma geliştirilmiştir.

Apriori Algoritması

Algoritmanın ismi, sık görülen nesne kümelerin önsel bilgisini kullanmasından, diğer bir ifadeyle bilgileri bir önceki adımdan almasından dolayı bir önceki (prior) anlamına gelen “apriori” dir.

Apriori özelliği: Apriori algoritmasının temel yaklaşımı, “Eğer k nesneden oluşan nesne setleri kümesi en küçük destek kriterini sağlıyorsa, bu kümenin alt kümeleri de en küçük destek kriterini sağlar.” şeklindedir.

Destek Bazlı Budama Özelliği : Apriori özelliğinin aksine, “Eğer bir alt küme sık görülen nesne kümesi değil ise, onun bütün üst kümeleri de sık görülen nesne kümesi değildir” temel yaklaşımına sahiptir. Böylece belirlenen destek eşik değerini geçemeyen az elemanlı kümelerin üst kümeleri de destek eşik değerini geçemeyeceği için değerlendirme dışı bırakılır.

Örneğin; I={a,b,c,d} nesne kümesi için, şayet {c, d} nesne kümesi bir sık görülen nesne kümesi değil ise, bu kümenin elemanlarını içeren tüm üst kümeleri olan {a, c, d}, {b, c, d} ve {a, b, c, d} kümeleri de sık görülen nesne kümeleri değildir.

Apriori algoritması seviye mantığı arama olarak bilinen yinelemeli bir yaklaşım kullanır. Bu yaklaşımda k ögeli nesne setleri (k-1) ögeli nesne setlerinin birleştirilmesiyle oluşturulur. Böylece algoritma ile başlangıçta hesaplanan bilgiler daha sonraki yinelemelerde kullanıldığı için tekrar hesapların yapılması engellenmiş olur. Apriori algoritmasının, k-1 ögeli sık görülen nesne setleri kümesi L _k-1 kullanılarak k ögeli sık görülen nesne setleri kümesi L _k ’nın elde edilmesi iki adımda gerçekleştirilir. Bunlar birleştirme ve budama adımlarıdır.

Konu ile ilgili örnek S.116-120’de incelenebilir.

İlişki Kuralları R Çözümü

R ile ilişki kuralı oluşturabilmek için arules paketinin R’de kurulması ve hafızaya yüklenmesi gerekir. arules paketi içerisinde yer alan apriori( ) fonksiyonu yardımıyla güçlü ilişki kuralları oluşturulur.

apriori() fonksiyonunun temel parametreleri ilişki kurallarının oluşturulabilmesi için elde edilen tüm işlemleri (alışverişleri) barındıran veri değişkenini ifade eden data ve özellikle destek ve güven eşik değerleri vb. kısıtlamalara ilişkin eşik değerlerinin belirlendiği parameter’dır. Veri girişi standart veri girişlerinden herhangi birisi ile yapılabilir. Ancak girilen verinin apriori() fonksiyonu ile işlenebilmesi için işlemlerden oluşan veritabanı formatına dönüştürülmesi gerekir. Veri dönüşümü için help(“transactions”) komutundan ve fonksiyon ile ilgili yardım için ise, help(“apriori”) komutundan yararlanılabilir.