Ünite 4: Benzerlik ve Uzaklık Ölçüleri

Giriş

Genel bir tanımı olmamasına rağmen, iki nesne arasındaki benzerlik, iki nesnenin birbirine benzeme derecesinin sayısal bir ölçüsü olarak tanımlanabilir. Veri madenciliği çerçevesinde ise benzerlik genellikle nesnelerin özelliklerini temsil eden boyutlara sahip bir uzaklık olarak tanımlanabilir. Dolayısıyla, benzerlikler birbirine daha çok benzeyen nesne çiftleri için daha yüksektir. Benzerlikler temel olarak [-1,1] arasında bir sayısal değer ile ifade edilebilmelerine rağmen, genellikle normalleştirilerek [0,1] arasında ölçeklendirilirler. Bu durumda “0” nesneler arasında hiç benzerliğin olmadığını, “1” ise ilgili nesnelerin tam benzer olduklarını, bir diğer ifadeyle aynı (özdeş) nesneler olduklarını ifade eder.

İki nesne arasındaki uzaklık ise iki nesnenin birbirinden farklılık derecesinin sayısal bir ölçüsüdür. Çoğunlukla, uzaklık kavramı farklılık kavramının yerine kullanılmasına rağmen aslında uzaklık, farklılıkların özel bir sınıfını ifade etmek için kullanılır. Farklılık, çeşitli özelliklere dayalı olarak iki nesne arasındaki zıtlık ya da uyumsuzlukların bir ölçümü olarak nitelendiğinde, uzaklık iki nesne arasındaki düzensizliğin veya bozukluğun bir ölçüsü olarak düşünülebilir. Kısaca uzaklık ölçüleri yardımıyla iki nesne arasındaki farklılığın derecesi ölçülmektedir.

Tanım (Uzaklık): X bir küme olmak üzere d: X x X ? R şeklinde tanımlanan bir fonksiyon, tüm x, y ? X için;

1. d(x, y) = 0, x = y ise (Özdeşlik)
2. d(x, y) ? 0 (Negatif olmama)
3. d(x, y) = d(y, x) (Simetri)

koşullarını sağlıyorsa d, X üzerinde bir uzaklık olarak adlandırılır. Bu koşullara ilave olarak eğer tüm x, y, k ? X için;

iv. iv. d(x, y) ? d(x, k) + d(k, y) (Üçgen eşitsizliği)

koşulu da sağlanıyor ise d, X üzerinde metrik uzaklık olarak adlandırılır.

Tanım (Benzerlik): X bir küme olmak üzere s: X x X ? şeklinde tanımlanan bir fonksiyon, tüm x, y ? X için;

i. s(x, y) = s(y, x) (Simetri)
ii. s(x, y) = 1, x = y ise (0 ? s ? 1) (Maksimum benzerlik)

koşullarını sağlıyorsa s, X üzerinde benzerlik olarak adlandırılır.

Hesaplamalar sonucunda elde edilen benzerlik değeri arttıkça iki nesne arasındaki benzerliğin de arttığı anlaşılırken bunun tam tersine elde edilen uzaklık değeri azaldıkça bu iki nesne arasındaki benzerliğin arttığı anlaşılmaktadır.

Dönüşümler

Dönüşümler genellikle benzerlik ve uzaklıklara ilişkin ölçüm değerlerinin birbirlerine dönüştürülmesinde veya her ikisi için farklı aralıklarda elde edilmiş ölçüm değerlerinin [0,1] gibi belirli bir aralık içerisinde ölçeklendirilmesi amacıyla kullanılırlar. Örneğin, elde edilen benzerlik ölçüm değerleri [1,100] aralığında yer alsın. Bir bilgisayar yazılımı aracılığı ile ilgili benzerlik değerleri kullanarak sınıflama veya kümeleme gibi farklı analizler yapmak istenebilir. Bilgisayar yazılımının kullandığı algoritma gereği sadece uzaklık ölçüm değerleri elde edildiyse veya [0,1] aralığına standartlaştırılmış benzerlik değerleri üzerinden işlem yapılmışsa bu tür durumlarda istenilen değerleri elde etmek için dönüşüm yapmak durumunda kalınabilir.

Birçok veri madenciliği uygulamasında özellikle benzerlik ölçüm değerlerinin [0,1] aralığında tanımlanmış veya bu aralıktaki değerlere dönüştürülmüş olması beklenir. Sonlu bir aralıkta değerler alan benzerlik ölçüm değerleri [0,1] aralığına uyacak şekilde dönüştürülmek istendiğinde,

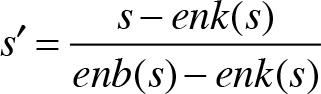
eşitliğinden yararlanılır. Eşitlik yardımıyla elde edilecek s’ değeri, dönüştürülmesi istenilen s benzerlik ölçüm değerinin [0,1] aralığına düşen değerini ifade eder.

Birçok alanda gereken analizleri yapabilmek ve sonuca ulaştırabilmek için geliştirilen çeşitli paket programlar mevcuttur. Elbette ki farklı paket programlar farklı algoritmalar kullanabilmektedir. Dolayısıyla farklı paket programların girdileri de çıktıları da farklı olabilmektedir. Bunun yanı sıra farklı benzerlik ve uzaklık ölçüleri de farklı aralıklarda sonuçlar vermektedir. Tüm bu nedenlerden dolayı gerek benzerlik ve uzaklık ölçülerini birbiri cinsinden ifade edebilmek için gerekse ölçüm değerlerini belirli aralıklarda ifade edebilmek için bir takım dönüşümler kullanılmaktadır.

Basit Nitelikler Arasındaki Yakınlık

Bir dizi niteliğe sahip nesnelerin yakınlığı, nesnelerin her bir niteliği için elde edilecek yakınlıklarının birleşimi olarak tanımlanır.

Şayet iki nesne sınıflayıcı bir nitelik açısından değerlendirilmeye çalışılıyorsa bu iki nesnenin ilgili nitelik açısından aynı olup olmadıklarından başka bir bilgi verilemez. Bu durumda benzerlik değeri, nesneler ilgilenilen nitelik bakımından aynı ise “1” olurken farklı ise “0” değeri ile ifade edilir. Uzaklık değeri ise benzerliğin tam tersi şekilde ifade edilir. Yani nesneler ilgilenilen nitelik bakımından aynı ise ilgili uzaklık değeri “0” olurken farklı ise “1” değerini alır. Örneğin bir güvercin ile arı uçma yetileri bakımından karşılaştırıldığında benzerlik değeri “1” olurken büyüklük bakımından karşılaştırıldığında ise benzerlik değeri “0” olacaktır.

Nesnelerin niteliklerine göre benzerlik ve uzaklık formülleri.

Benzerlik ve Uzaklık Ölçüleri

Birim ya da değişkenler arası benzerlik ya da uzaklık değerleri hesaplanırken geometrik yaklaşımlardan yararlanılır. Geometride koordinat sistemindeki iki nokta arasındaki en yakın uzaklık Pisagor bağıntısına göre elde edilir. Dolayısıyla koordinat sisteminde yer alan A ve B noktaları arasındaki doğrusal uzaklık, A noktasının koordinat değerleri A(x ₁ , y ₁ ) ve B noktasının koordinat değerleri B(x ₂ , y ₂ ) olmak üzere Pisagor bağıntısına göre;

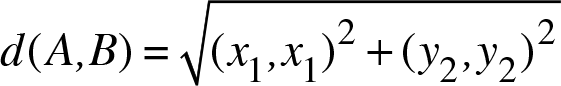
Nicel Değişkenler İçin Yakınlık Ölçüleri

Nicel değişkenlerden elde edilen gözlem değerleri arasındaki yakınlığın belirlenmesinde Öklid uzaklığı, Karesel Öklid uzaklığı, Karl Pearson uzaklığı, Manhattan uzaklığı, Minkowski uzaklığı, Mahalanobis uzaklığı, Korelasyon uzaklığı ve Açı sal benzerlik ölçülerinden yararlanılır.

Öklid ve Karesel Öklid Uzaklığı: Uzaklık ölçüleri arasında en yaygın kullanılan uzaklık ölçüleri Öklid ve Karesel Öklid uzaklık ölçüleridir. Her biri p tane nicel değişken içeren x _i ve x _j nesneleri arasındaki Öklid uzaklığı,

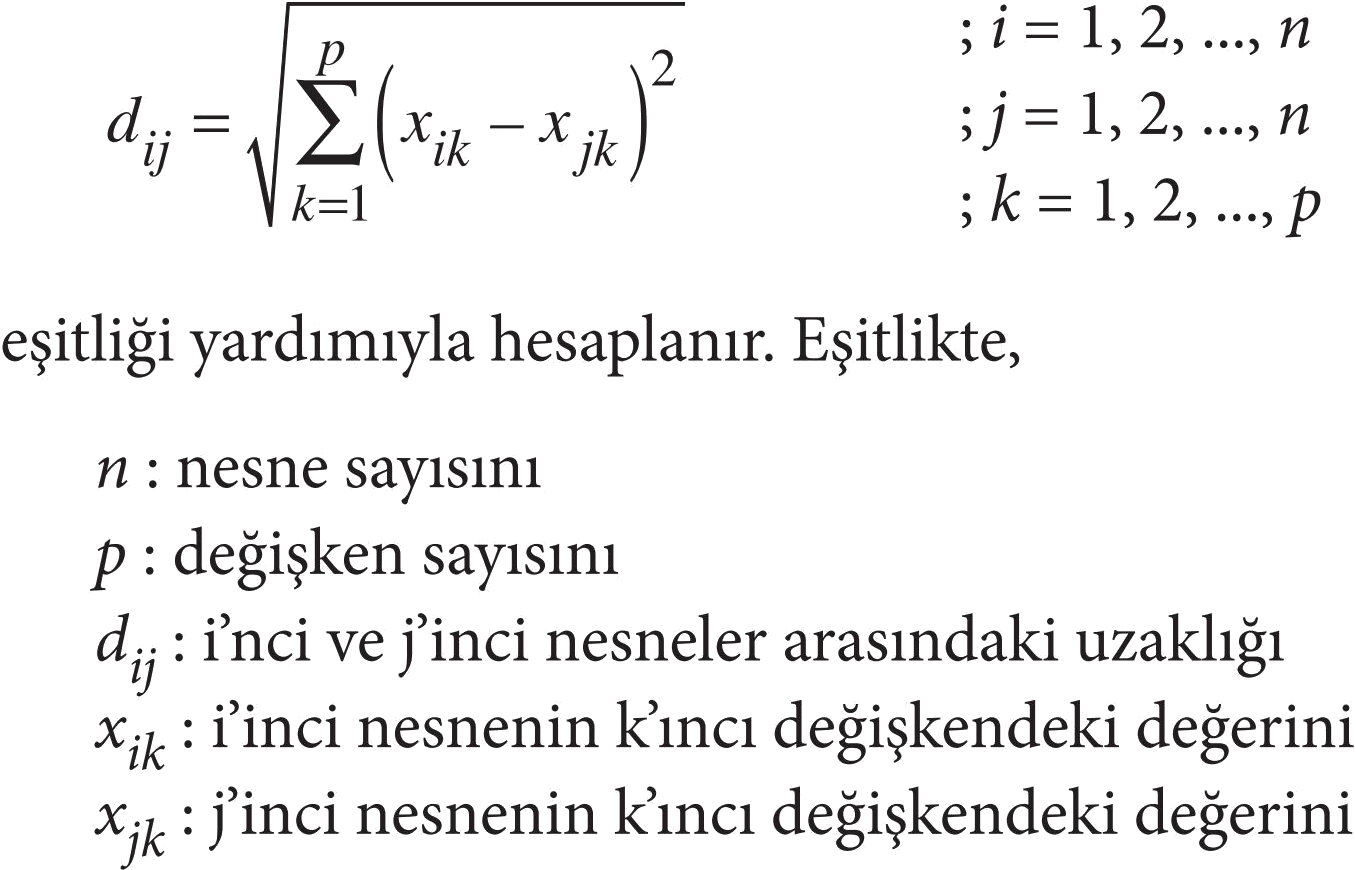
ifade eder.

Öklid uzaklığı, i’inci ve j’inci nesnelerin p tane değişken için farklarının kareleri toplamının karekökü alınarak elde edilir. Öklid uzaklığı hesaplanırken veriler kullanılır. Dolayısıyla farklı ölçekler ve değişkenlerin farklı ölçü birimleri ile ölçülmüş olması, hesaplanacak uzaklık değerini etkileyecektir.

Karesel Öklid uzaklığı ise Öklid uzaklığına benzer biçimde hesaplanır. Tek farkı değişkenlere göre toplam uzaklığın karekök alınmadan hesaplanmasıdır. Yani Öklid uzaklığının karesidir. Karesel Öklid uzaklığı,

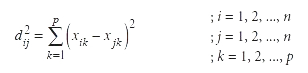
eşitliği yardımıyla hesaplanır. Karesel Öklid uzaklığının hesabında karekök alınmadığından Öklid uzaklığına göre veri kümesi içerisinde yer alan aykırı değerlere (outliers) daha fazla ağırlık verme eğilimindedir.

Karl Pearson Uzaklığı: Karl Pearson uzaklığı, Öklid uzaklığının değişkenin varyansına oranlanması ile elde edilen bir uzaklıktır. Bu özelliğinden dolayı standartlaştırılmış Öklid uzaklığı olarak da bilinmektedir. Öklid uzaklığı yaygın olarak tercih edilen bir uzaklık ölçüsü olmasına rağmen, değişkenlerin ölçü birimlerinden kolaylıkla etkilenmektedir. Dolayısıyla farklı ölçü birimlerine sahip değişkenler söz konusu olduğunda hesaplama yapmadan önce değişkenlerin standartlaştırılması gerekir. Böyle bir durumda ölçü birimi farklılıklarını ortadan kaldırmak amacıyla Öklid uzaklığının standartlaştırılmış şekli olan Karl Pearson uzaklığı,

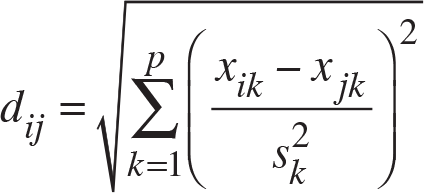
eşitliği yardımıyla hesaplanır.

Manhattan (City-Block) Uzaklığı: Bir diğer sıklıkla kullanılan uzaklık ölçüsü ise Manhattan uzaklığıdır. Manhattan (City Block) uzaklığı, birimler arası farkların mutlak değerinin toplamı alınmak suretiyle

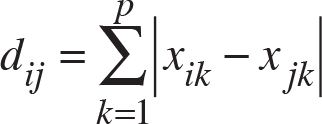
eşitliği yardımıyla hesaplanmaktadır.

Minkowski Uzaklığı: n sayıda birim ve p sayıda değişken ile çalışılırken birimler ya da değişkenler arasındaki uzaklıkları hesaplamak için kullanılan genel bir uzaklık ölçüsüdür. L _? norm olarak da bilinen Minkowski uzaklığı,

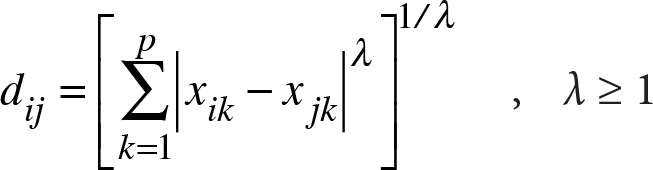
eşitliği yardımıyla hesaplanır.

Açısal Benzerlik: Açısal benzerlik, iki vektör arasındaki açı farkının kosinüsünün bu iki vektör arasındaki uzaklık olarak alınması suretiyle değişkenler arasındaki benzerliğin belirlenmesine yönelik bir benzerlik ölçüsüdür. İki vektör arasındaki açı farkı sıfır olduğunda yani vektörler birbirlerine paralel olduklarında kosinüs değeri 1 olurken bu iki vektör arasındaki açı farkı 90° olduğunda yani vektörler birbirlerine dik olduklarında kosinüs değeri 0 olur. Dolayısıyla elde edilen değerin 1 olması değişkenler arasında tam bir benzerliğin olduğunun, 0 olması ise değişkenlerin hiç benzerliğin olmadığının göstergesi olmaktadır.

Açısal benzerlik, özellikle belge ve çoklu ortam nesnelerinin kıyaslanmasında ve metin madenciliğinde kullanılmaktadır.

Mahalanobis Uzaklığı: Sürekli değişkenler arasındaki yakınlığın belirlenmesinde kullanılan bir diğer ölçü ise Mahalanobis uzaklığıdır. Bu uzaklık ölçüsü, iki vektör veya değişken arasındaki uzaklığın belirlenmesinde verilerin kovaryans yapılarını da dikkate almaktadır. Her biri n boyutlu x ve y gözlem vektörleri arasındaki Mahalanobis uzaklığı,

d _xy = D ² = ( x – y ) ^T S ^–1 ( x – y )

eşitliği yardımıyla hesaplanır.

İki Sonuçlu (Binary) Değişkenler İçin Yakınlık Ölçüleri

İki sonuçlu (binary) değişkenler, ölçüm değerleri sınıflama yoluyla elde edilen nitel değişkenlerdir. Bu değişkenler sadece evet/hayır, var/yok, erkek/kadın, doğru/yanlış gibi değerler alırlar. İki sonuçlu değişkenler için benzerlik veya uzaklık ölçüm değerlerin hesaplanabilmesi için her bir nesne incelenen değişkenlere ilişkin aldığı değerlerden oluşan bir vektör şeklinde ifade edilir. İki sonuçlu değişkenler içeren gözlem çiftleri arasındaki yakınlığın belirlenmesinde Öklid, Karesel Öklid, Büyüklük Farkı (Size Difference), Örüntü Farkı (Pattern Difference), Lance ve Williams Uzaklık Ölçüsü, Biçim Farkı (Shape Difference) ve Jaccard Benzerliği (Jaccard Similarity) gibi birçok benzerlik ya da uzaklık ölçülerinden yararlanılmaktadır. Bu ölçüler temel olarak eşleştirmeye dayanan ölçüler olduklarından, hesaplama yapmadan önce kontenjans ya da diğer adıyla çapraz sınıflama tablosunun oluşturulması gerekir. İki yönlü sınıflama tablosu olarak da adlandırılan kontenjans tablosu, iki sonuçlu değişkenler içeren nesne çiftinin karşılıklı eşleşen değerlerinin tekrar sayılarından oluşan tablodur.

Bundan dolayı, benzerlik ve uzaklık ölçüleri temel olarak verinin tipine göre farklılaşmakta ve farklı veri türleri için farklı ölçüler hesaplanmaktadır. Verinin sahip olduğu özellikler ve karşılaştırılacak nesnenin özelliklerine bağlı olarak başlıca kullanılan benzerlik ve uzaklık ölçüleri de farklı algoritma ve hesaplama yöntemlerine sahip olmaktadır.