Ünite 2: Doğrusal Programlama

Giriş

Yöneylem araştırmasının en gelişmiş ve yaygın uygulama alanını doğrusal programlama oluşturur. Doğrusal programlama, belirli bir amaca ulaşmak için, bazı kısıtlayıcılar altında kıt kaynakların en verimli şekilde kullanılmasını sağlayan bir matematiksel yöntemdir. Bu şekilde varılmak istenen amaç, kâr maksimizasyonu (en büyükleme) veya maliyet minimizasyonu (en küçükleme) olarak belirlenebilir. Doğrusal programlamada “doğrusal” sözcüğü fonksiyonların doğrusallığını, “programlama” ise planlama işlemini ifade eder. Doğrusal programlama, tüm uygun seçenekler arasından optimum (en iyi) sonucun elde edilmesini sağlayan planlama faaliyetlerini içermektedir.Doğal olarak böyle bir programlama sürecinde, önce gerekli veriler toplanır, problem modellenir ve daha sonra modelin çözümü araştırılır. Doğrusal programlama modeli kurulurken amacın, değişkenler arasında ilişkilerin ve kullanılacak kıt kaynakların tanımlanması gerekir.

Doğrusal programlamanın uygulama alanları;

• Ulaştırma ve lojistik problemleri,
• Endüstriyel üretim planlaması ve envanter (stok) kontrolü
• Personel programlaması
• Beslenme (diyet) problemleri
• Karışım problemleri
• Tarımsal planlama
• Finansal planlama
• Yatırım planlaması
• Sağlık sistemleri
• Askeri planlama
• Trafik planlaması
• Atama problemleri
• Reklam seçimi problemleri
• Karışım problemleri

şeklinde sıralanabilir.

Görüldüğü üzere, geniş bir uygulama alanına sahip olan doğrusal programlama, ayrıca işletmelerin karşılaştığı darboğazların giderilmesinde, kıt kaynakların etkin kullanımı ve bunların gölge fiyatlarının belirlenmesi ile en uygun çözümlere ulaştıracak politikaları saptamada kullanılmaktadır.

Doğrusal Programlamanın Varsayımları

Gerçek hayatta karşılaşılan çoğu karar problemi için doğrusal karar modeli geliştirilebilir. Bir problem için karar modeli geliştirmek ve kurmak gerçek sistemi matematiksel olarak ifade etmekle eşdeğerdir. Bu işlem yapılırken bilgi kaybı kaçınılmazdır. Önemli olan en az bilgi kaybı ile dönüşümü gerçekleştirebilmektir. Bu nedenle modelden tutarlı sonuçlar elde edilebilmesi için doğrusallık varsayımı, toplanabilirlik varsayımı, bölünebilirlik varsayımı, belirlilik varsayımı kabul edilir.

Doğrusallık varsayımı , modelin amaç fonksiyonu ve kısıtlayıcı fonksiyonları ile ilgilidir. Doğrusallık varsayımı, işletmenin girdileri ile çıktıları arasında doğrusal bir ilişkinin olduğunu gösterir. Üretim düzeyi artarken aynı oranda üretim girdileri de artar. Eğer, X _j ’inci eylem için amacın oluşumu doğrusallık özelliği gösteriyorsa, X _j’ nin her bir birim değerinin kâra katkısı c _j ise, X _j ’nin çözüm değerinin amaca katkısı c _j X _j kadar olur. Kısıtlar ve amaç fonksiyonu birinci dereceden fonksiyonlar olmalıdırlar. Aksi takdirde, doğrusal olmayan programlama olarak değerlendirilir. Bu varsayım, her bir karar değişkeninin; gerek amaç fonksiyonu, gerekse tük kısıtlayıcılara etkisinin söz konusu değişkenin (X _j ) değeriyle doğru or,antılı olması gerektiğinin ifade eder.

Toplanabilirlik varsayımında doğrusal programlamada her fonksiyon, ilişkili olduğu faaliyetlerin, bireysel katkılarının toplamıdır. Karar değişkenlerine verilecek değerlere göre, her bir değişkenin sağladığı katkılar toplanıp toplam katkıyı, yani amaç fonksiyonunu, oluşturuyorsa toplanabilirlik varsayımı geçerlidir demektir.

Bölünebilirlik varsayımının sağlanabilmesi için modelin karar değişkenleri X _j ’ler, her türlü reel değerleri alabilmesi gerekir. Böylece, karar değişkenleri, bazı faaliyetlerin düzeyini gösterdiğinden, faaliyetlerin kesirli düzeylerde çalışabileceği varsayılır. Bazı durumlarda girdi ve çıktılar bölünemez olarak ele alınmalıdır, karar değişkenlerinin tamamının veya bazılarının tam sayı olması gerekebilir. Böyle durumlar, tam sayılı programlama adı altında ele alınır.

Belirlilik varsayımında doğrusal programlama modelindeki tüm parametrelerin, yani amaç fonksiyonu katsayıları-c _j , sağ taraf sabitleri-b _i ve teknoloji katsayıları a _ij ’lerin biliniyor olduğu varsayımıdır. Parametre değerlerinin kesin olarak biliniyor olması varsayımı, modelin deterministik model olduğunu belirtir. Bir problemde, karar değişkenleri ve parametrelerle ilgili olarak; doğrusallık, toplanabilirlik, bölünebilirlik ve belirlilik varsayımları geçerli ise bu problem doğrusal programlama problemi olarak modellenip çözülebilir. Parametre değerlerinden kesin değerleri bilinmeyenler için tahmin yoluna gidilebilir. Daha sonra matematiksel modelleme aşamasına geçilmelidir.

Doğrusal Programlamada Model Kurma

Model kurma, sistemi oluşturan unsurların matematiksel terimlerle ifade edilmesidir. Model doğrusal programlama gibi standart bir matematiksel model halinde ifade edilebiliyorsa, bilinen algoritmalar yardımıyla çözümlenebilir. Bir problemin, doğrusal programlama modeli kurulurken önce karar değişkenleri tanımlanır, daha sonra amaç fonksiyonu ve kısıtlayıcılar formüle edilir.

Karar değişkenlerinin belirlenmesi , Bir problemin doğrusal programlama modelinin kurulmasına, öncelikle karar değişkenlerinin tanımlanmasıyla başlanır. Karar  değişkeni: bir problemde karar vericinin kontrolü altında olup, değeri araştırılan eylemler, karar değişkenleridir. Karar değişkenleri, alınacak kararlara ilişkin faaliyetlerin düzeyini göstermektedir.

Karar değişkenleri genellikle X _j sembolü ile gösterilir.

X _j : j’ inci üründen üretilecek (veya taşınacak) miktar anlamındadır. (j=1,2,….,n)

Amaç fonksiyonunun belirlenmesi , Herhangi bir doğrusal programlama probleminde karar verici, karar değişkenlerini içeren fonksiyonu maksimum veya minimum yapmak ister. Maksimum veya minimum yapılmak istenen fonksiyona, amaç fonksiyonu adı verilir.

Doğrusal programlama modelinden beklenen sonucun alınabilmesi için, amacın açık olarak bilinmesi ve nicel olarak yazılımı gerekmektedir.

Modelin amaç fonksiyonu yazılırken;

Karar değişkenleri: X ₁ , X ₂ , ..., X _n

Birim kâr veya maliyet katsayıları c ₁ ,c ₂ ,….,c _j ,…,c _n ile gösterildiğinde

Amaç fonksiyonu:

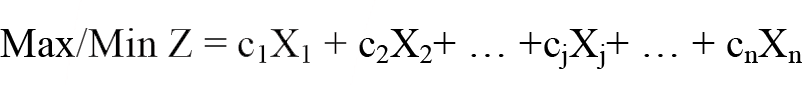
Kısıtlayıcıların belirlenmesi , Ekonomide üretim kaynakları veya üretim faktörleri sınırlıdır. Bir işletmenin elindeki makine kapasitesi, teknolojisi, işgücü, enerji, sermaye, hammadde, yarı mamul madde, malzeme gibi üretim faktörleri ile ürünlerine olan talep sınırlıdır. Dolayısıyla karar değişkenlerinin miktarı da sınırlı olacaktır. Önemli olan, bu kısıtlayıcılar altında amaç fonksiyonunu sağlayan ürünler üretmektir.

İşletmenin faaliyetlerinde,

bi: i’inci kaynak miktarı, (i=1,2,3, … m)

aij: bir birim Xj için gerekli i’inci kaynak miktarı (Xj’lerin i’inci kısıttaki teknoloji katsayıları) sembolleri ile gösterilir. Bu durumda doğrusal kısıtlı fonksiyonların genel hali aşağıdaki gibidir,

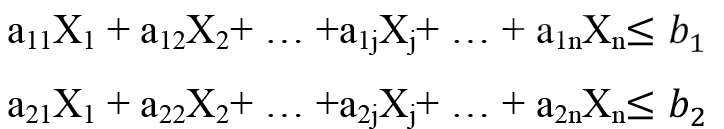
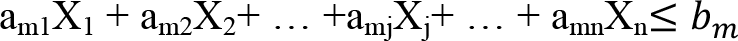
Kısıtlayıcılardaki karar değişkenlerinin katsayıları (a _ij ), farklı ürünlerin üretiminde kullanılan teknolojiyi yansıttığı için, teknolojik katsayılar adı verilir. Kısıtlayıcıların sağ taraf sabitlerini oluşturan bi’ler elverişli kaynak miktarını temsil eder. Bu kaynak miktarları kısıtlayıcı fonksiyonuna göre her zaman sınırlı olmaz. Bazen karar değişkenlerinin istediğinden fazla veya tam eşitlikte olabilir. Bu nedenle kısıtlayıcı denklemler, “=” eşitlik şeklinde olabileceği gibi, eşitsizlik şeklinde de olabilir. Kısıtlayıcı fonksiyonlar genel olarak;

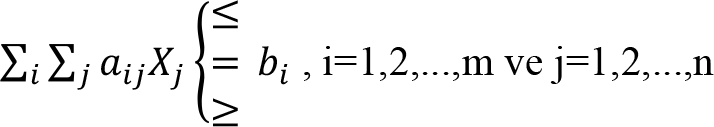
olarak ifade edilir.

Doğrusal programlama probleminin matematiksel modelini tamamlamak için her bir karar değişkeninin negatif olmama varsayımını sağlaması gerekir. Karar değişkeni Xj’nin sadece pozitif değerli olduğu varsayılırsa , “ X _j ? 0” işaret kısıtı modele eklenir.

Özetlemek gerekirse, doğrusal programlama modelinin matematiksel yazılımı,

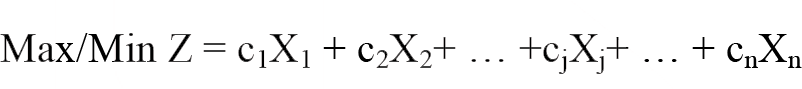
Kısıtlayıcılar

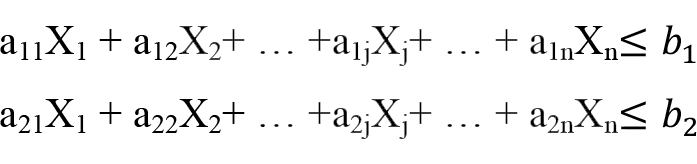
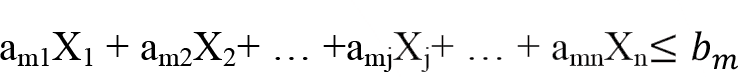
olarak verilir.

Doğrusal Programlamanın Model Kurma Uygulamaları

Bir karar problemi için model geliştirme öncesinde amacın, karar değişkenlerinin ve parametrelerin tanımlanmış olması gerekir.

Doğrusal programlama üretim planlamasında, tarım planlamasında, karışım problemlerinde, ulaştırma ve lojistik problemlerde, personel programlamasında, beslenme problemlerinde, reklam seçim problemlerinde çözüm bulmak için sıklıkla kullanılır.

Doğrusal programlamanın en yaygın kullanıldığı alanlardan birisi, üretim işletmelerin de maksimum karlı veya minimum maliyetli üretim bileşenlerini belirlemede kullanılmasıdır.

Tarım sektöründe çiftçiler için en önemli problem, en çok karı sağlamak için eldeki arazinin ürün türlerine göre taksimi nasıl olmalıdır? sorusudur. Ayrıca arazinin üretim verimliliğinin bilinmesi halinde, hangi üründen ne kadar üretim elde edilebileceği de belirlenebilmektedir.

Karışım problemlerinde uygulanmasının yanı sıra ulaştırma ve lojistik problemlerinde de uygulanır. Ayrıca Doğrusal programlama işletmelerde minimum maliyetli işgücü gereksinimini karşılamada, eğitim öğretim planlaması gibi konularda etkin şekilde kullanılmaktadır.

Doğrusal programlama ile modellenip, çözülen ilk ekonomik problemden biri de diyet problemidir. İlk önceleri diyet probleminin, sayısal bir örneği alınarak çözümü araştırılmış, daha sonra beslenmeyle ilgili ilginç uygulamaları yapılmıştır. Günümüzde toplu beslenme yerlerinde (öğrenci veya işçi yemekhanelerinde), büyük şantiyelerde, gemi-denizaltı vb. yerlerde beslenme planlaması doğrusal programlama ile yapılmaktadır.

Günümüz işletmeleri ürün ve hizmetlerini müşterilerine tanıtmak ve talebi artırmak için etkin reklam kampanyaları yürütürler. Reklamın amacına ulaşmasına yönelik olarak, etkili olacak reklam seçiminde doğrusal programlama kullanılmaktadır.