Ünite 3: Doğrusal Programlama Modellerinin Çözümü: Grafik Çözüm Tekniği

Giriş

Doğrusal programlama, amaç fonksiyonunu etkileyen kısıtlayıcıların bulunması ve bunların doğrusal eşitlik ve eşitsizlikler olarak verilmesi durumunda, amaca en iyi bir biçimde ulaşılması için, kıt kaynakların en verimli şekilde kullanılmasını sağlayan bir matematiksel yöntemdir. Böyle bir programlama sürecinde, önce gerekli veriler toplanır, probleme ait bir model kurulur ve modelin çözümü araştırılır. Bu çözümler, kurulmuş olan modelin yapısına bağlı olarak tek bir çözüm, seçenekli çözüm olabilir veya modelin hiçbir çözümü bulunmayabilir. Karar vericinin farklı seçenekler arasından, işletmesi için en uygun olanını, uygulamaya koyması gerekir. Bazı durumlarda, modele dahil edilememiş çeşitli etkenlerden dolayı, optimum çözüm yerine, ona en yakın olan başka bir çözümün benimsenmesi söz konusu olabilir.

Grafik Çözümünün Temel Esasları

Bir doğrusal programlama modelinin tüm kısıtlarını sağlayan her X vektörüne, X=[X ₁ , X ₂ , … X _j , … X _n ] uygun çözüm denir.

Uygun çözümlerin oluşturduğu kümeye,

Uygun Çözüm Alanı (UÇA) denir. Uygun Çözün Alanı = {X | AX?b, X?0 }

Burada aşağıda gösterildiği şekilde A-matris ve b-sütun vektörüdür.

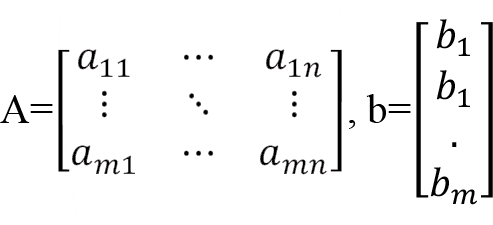
Karar modeli açısından her uygun çözüm bir seçenek, Uygun Çözüm Alanı ise seçenekler kümesi anlamındadır. Uygun Çözüm Alanı üzerinde Xj’lere göre, amaç fonksiyonunun maksimum (en büyük) veya minimum (en küçük) değerini aldığı Xj’lere optimum (en iyi) çözüm seti, amaç fonksiyonuna karşı gelen değerine optimum (en iyi) değer denir.

Uygun Çözüm Alanı dışbükey(konveks) bir alandır. Dışbükey alanın temel özelliği, bu alan içinde iki nokta ele alınıp bir doğru parçasıyla birleştirildiğinde, birleştiren doğru parçasının tamamının alan içinde kalmasıdır. Bir anlamda Uygun Çözüm Alanı kümesindeki herhangi iki nokta çiftini birleştiren doğru parçası, tamamen Uygun Çözüm Alanı kümesinde ise, uygun çözüm alanı dışbükey bir kümedir. Söz konusu doğru parçasının bir kısmını içine almayan küme ise, içbükey (konkav) kümedir.

Uç (köşe) Nokta Teoremi, Grafik üzerinde Uygun Çözüm Alanının (UÇA) farklı iki noktasının dışbükey birleşimi olarak yazılamayan noktası varsa, buna uç nokta veya köşe nokta denir. Düzlemde bir üçgenin, bir karenin köşeleri uç (köşe) noktadır. Şu halde, amaç fonksiyonu maksimizasyon (en büyükleme) veya minimizasyon (en küçükleme) yönünde olan bir doğrusal programlama modelinin:

i. Eğer modelin optimum (en iyi) çözümü varsa, bu çözüm Uygun Çözüm Alanının bir köşe noktasındadır.

ii. Amaç fonksiyonu optimum (en iyi) değerini birden çok köşe noktasında alıyorsa, bu noktaların her dışbükey birleşimi de optimum(en iyi) çözümdür.

Grafik Çözümünün Adımları

Grafik çözüm tekniği ile genellikle iki karar değişkenli modellerin çözümü mümkün olur. Uygulamada genellikle çok sayıda değişken ve kısıtlayıcı içeren modellerle karşılaşılır. Ancak burada incelenecek olan karar modellerinde iki değişken bulunacaktır. Yine de iki değişkenli modellerin grafik çözümleri, doğrusal programlamanın mantığının daha kolay kavranmasına önemli ölçüde katkıda bulunur. Çünkü çok daha karmaşık modellerin çözümünde, yine aynı mantık yol gösterecektir.

Modelin iki karar değişkeni olduğunda, kısıtların her biri düzlemde bir doğru oluşturur. Bu doğrunun ikiye ayırdığı düzlemin bir bölgesi, ilgili kısıttı sağlayan (X ₁ , X ₂ )‘i değerlerini verir. Modelin tüm kısıtlayıcı fonksiyonları aynı koordinat sisteminde çizilerek, her bir kısıttın sağlanan bölgeleri taranırsa, kısıtları birlikte gerçekleştiren (X ₁ , X ₂ ) ikilileri, yani “Uygun Çözüm Alanı (UÇA)” taranmış bölge olarak ortaya çıkar.

Bu açıklamalar ışığında bir doğrusal programlama modelinin grafik çözümünde yapılacak işlemler şöyle sıralanabilir.

i. Her bir kısıt eşitlik olarak ele alınıp, karşı gelen doğrunun grafiği çizilerek, kısıtı sağlayan yönü (bölge) işaretlenir. Tüm kısıtları aynı anda sağlayan bölge taranarak “Uygun Çözüm Alanı (UÇA)” olarak belirlenir.

ii. Uygun Çözüm Alanının köşe noktalarında karar değişkenlerinin ve amaç fonksiyonunun değeri hesaplanarak amacı sağlayan köşe, optimum çözüm noktası olarak ilan edilir.

iii. Optimum çözüm seti (amaç fonksiyonu ve karar değişkenlerinin değeri) yazılarak çözüme ulaşılmış olur.

Maksimizasyon Modelinin Grafik Çözümü

İki değişken içeren modellerde, iki boyutlu uzayda grafik çözüm tekniği ile çözülebilir.

Kısıtlayıcıların grafik çizimi , Doğrusal karar modelinin optimum çözümünü bulmak için öncelikle Uygun Çözüm Alanının (UÇA) belirlenmesi gerekmektedir. İlk adımda modelin kısıtlayıcıları olan doğrusal eşitsizliklerin grafiğini çizmek gerekir. Bütün doğrusal programlama modellerinde negatif olmama kısıtlayıcıları (X ₁ , X ₂ ? 0) olabileceğinden, öncelikle bu kısıtların sağlanması ile başlamak gerekir. Koordinatlar ekseninde, uygun çözüm alanının hangi bölümde yer aldığı belirlenir.X ₁ ve X ₂ değişkenlerinin çözüm değerlerinin anlamlı olabilmesi için, negatif olmayan değer almaları gerekir.

Doğrusal kısıtlayıcıların veya eşitsizliklerin grafiğini çizmek için iki adım izlenir.

Adım 1: Doğrusal eşitsizlikler eşitlik halinde ifade edilerek, bunların sınırlarını gösteren, doğrular çizilir.

Adım 2: Doğrunun hangi tarafının eşitsizliğe uygun düştüğü belirlenir.

İki değişkenli doğrusal denklemlerin grafiğini çizmenin en kolay yolu, çizilecek doğrunun yatay ve dikey ekseni kestiği noktaları bulmak ve bu noktaları bir doğruyla birleştirmektir.

Uygun çözüm alanının belirlenmesi , Uygun Çözüm Alanının sınırları, kısıtlayıcı doğrusal denklemlerle ifade edilen, çizilen doğrusal eşitsizliklerin grafiği ile belirlenir.

Uygun Çözüm Alanı sınırları içinde (sınırlayan çizgiler dâhil) herhangi bir (X ₁ , X ₂ ) noktası, karar modelinin bütün kısıtlarını matematiksel olarak sağlar.

Optimum çözümün bulunması , Doğrusal programlamada optimum çözüm her zaman, Uygun Çözüm Alanının köşe noktalarındadır.

Maksimizasyon problemlerinde, orijine (0, 0) en uzak köşe noktalarında en iyi çözüm araştırması yapılması, bizleri daha fazla hesaplamadan kurtarır, böylece daha çabuk optimum çözüme ulaşılır.

İki değişkenli doğrusal denklemlerin grafiğini çizmek için, çizilecek doğrunun yatay ve dikey ekseni kestiği noktalar bulunur.

Uygun çözüm alanında her noktanın (X ₁ , X ₂ ) değerleri problem için bir uygun çözümü verir. Optimal çözüm ise, uygun çözüm alanının köşe noktalarının birisindedir. Bunun için köşe noktalarının her birinin, (X ₁ , X ₂ ) değerleri amaç fonksiyonunda yerine konur.

Minimizasyon Modelinin Grafik Çözümü

Grafik çözüm tekniği ile maksimizasyon problemleri çözülebileceği gibi, benzer şekilde minimizasyon (en küçükleme) problemleri de çözülebilir.

Minimizasyonun grafik çözümünde de maksimizasyon probleminde izlenen adımlar geçerlidir.

Doğrusal karar modelinin optimum çözümünü bulmak için öncelikle Uygun Çözüm Alanının (UÇA) belirlenmesi gerekmektedir. İlk adımda modelin kısıtlayıcıları olan doğrusal eşitsizliklerin grafiğini çizmek gerekir. Bütün doğrusal programlama modellerinde negatif olmama kısıtlayıcıları (X ₁ , X ₂ ? 0) bulunduğundan, öncelikle bu kısıtların doyurulması ile başlamak gerekir. Koordinatlar ekseninde, uygun çözüm alanının hangi bölümde yer aldığı belirlenir. X ₁ ve X ₂ değişkenlerinin çözüm değerlerinin anlamlı olabilmesi için, negatif olmayan değer almaları gerekir.

Minimizasyon grafik çözümünde maksimizasyon probleminde izlenen adımlar aynen geçerlidir. Daha önce doğrusal programlamada karar modelinin optimum çözümü, uygun çözüm alanının köşe noktalarından birisi olabileceğine değinilmişti. Minimizasyon probleminde optimum çözüm, orijine(0,0) en yakın köşe noktalarında yer alır.

Grafik Çözümünde Özel Durumlar

Bir doğrusal karar modelinin çözümü, grafik çözüm tekniği ile araştırılırken bazı özel durumlardan birisiyle karşılaşılabilir.

1. Uygun çözüm alanı boş (uygun çözüm bulunmama),
2. Sınırsız Çözüm (amaç fonksiyonu uygun çözüm alanında sınırsız),
3. Seçenekli (çoklu) optimal çözüm.

Uygun çözüm alanı boş , Karar modelinin kısıtlarının grafiği çizildiğinde, uygun çözüm alanı oluşmuyor (boş) ise, problemin çözümü yoktur denir.

Uygun çözüm bulunmaması, problemin yapısından kaynaklanabileceği gibi, modelleme hataları da (bir kısıtlayıcının yönünün ters olması gibi) uygun çözüm alanının boş olmasına neden olabilmektedir.

Sınırsız çözüm , Bazı doğrusal programlama modellerinin amaç fonksiyonu değeri, uygun çözüm alanı üzerinde istenen yönde sonlu değilse, optimum değeri bulunamayacağından, sınırsız çözüm vardır denir. Bu durum karar vericiye hiçbir öneri getiremez. Sınırsız çözümün varlığı, grafik çözümde, grafik üzerinde kolaylıkla görülebilir.

Seçenekli optimal çözüm , Doğrusal programlama problemleri birden çok optimum çözüme sahip olabilir. Karar modelinin amaç fonksiyonunun optimum değeri, uygun çözüm alanında iki ayrı noktada aynı değeri alıyorsa, modelin seçenekli (alternatif) çözümü vardır denir.

Bir doğrusal programlama problemini matematiksel modelle ifade etmek, en iyi çözümün araştırılmasının yanı sıra, problemin yapısında veya parametrelerde meydana gelebilecek değişiklikleri analiz etme imkanı da sunar. Problemde iki karar değişkeni var ise, grafik çözümle tüm olası durumlar görülebilmekte ve analizler yapılabilmektedir. Uygulamada karşılaşılan problemlerde karar değişkeni ve kısıtlayıcı sayısı ikiden daha çoktur. Özellikle değişken sayısı ikiden çok olduğunda, grafik çözüm etkin bir analiz tekniği olmaz. Değişken ve kısıtlayıcı sayısı itibariyle büyük hacimli modellerin çözümünde etkin teknik olan Simpleks Çözüm Tekniği ile ele alınırlar.