Matematiksel İktisat Final 13. Deneme Sınavı

Toplam 10 Soru

Diğer "Matematiksel İktisat" Sınavları

PAYLAŞ:

1.Soru

Bir malın ters talep fonksiyonu p=250-3Q olduğuna göre, bu malın talep miktarı 80 iken talep edilen fiyatı ne olur?

10

20

30

40

50

2.Soru

Bir mal için talep fonksiyonu Q=20-4P şeklindedir. Buna göre Q=2 üretim düzeyinde marjinal maliyet aşağıdakilerden hangisine eşittir?

1

2

3

4

5

3.Soru

matrisinin evriği aşağıdakilerden hangisidir?

4.Soru

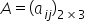"i ve j indislerinin toplamı" ve 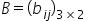"i ve j indislerinin farkı" olarak tanımlanmıştır. Buna göre A.B matrisi aşağıdakilerden hangisidir?

5.Soru

Yukarıda verilen üretim fonksiyonuna göre K=256 ve L=108 için marjinal teknik ikame oranı (MRTS) aşağıdakilerden hangisidir?

-7.11

-5.64

-6.75

-4.35

-8.90

6.Soru

olarak verilmiştir. Buna göre A ve B matrisleri arasında aşağıdaki işlemlerden hangisi yapılamaz?

A+B

A-B

A*B

3A+2B

7.Soru

Köşegen elemanları bire eşit olan skaler matrise ne ad verilir?

Skaler matris

Üçgensel matris

Alt üçgensel matris

Simetrik matris

Birim Matris

8.Soru

Bir piyasa için Qd=-2p+21 ve Qs=3p+6 şeklindeki arz ve talep denklemleri için verilmiştir. Bu piyasada dengeyi sağlayan arz-talep miktarları nedir?

p=2, Q=13

p=3, Q=15

p=2, Q=16

p=3, Q=20

p=5, Q=25

9.Soru

Amaç fonksiyonunun f(x,y) = 5x² + 6xy + 12y², kısıt fonksiyonunun ise g(x,y) = x + y = 120 olduğu durumda oluşturulan Lagrange fonksiyonu aşağıdakilerden hangisinde doğru ifade edilmiştir?

L(x,y,λ) = 5x² + 6xy + 12y² + x + y + 120

L(x,y,λ) = 5x² + 6xy + 12y² + λ( x + y + 120)

L(x,y,λ) = 5x² + 6xy + 12y² + λ(120 – x – y)

L(x,y,λ) = 5x² + 6xy + 12y² + λx + λy

L(x,y,λ) = 5x² + 6xy + 12y² + 120λ

10.Soru

fonksiyonunun x=0 noktasındaki türevi aşağıdakilerden hangisidir?

0

1

2

4

8