Yöneylem Araştırması Ara 11. Deneme Sınavı
Toplam 20 Soru1.Soru
Uygun C¸özüm Alanı, dışbükey(konveks) bir alandır. Doğrusal programlamada optimum çözüm her zaman, Uygun C¸özüm Alanının neresinde yer alır?
Uygun C¸özüm Alanı, dışbükey(konveks) bir alandır. Doğrusal programlamada optimum çözüm her zaman, Uygun C¸özüm Alanının neresinde yer alır?
|
Yatay eksende |
|
Kenar çizgilerinde |
|
Dış noktalarında |
|
Köşe noktalarında |
|
İç noktalarında |
Uygun C¸özüm Alanı, dışbükey(konveks) bir alandır. Doğrusal programlamada optimum çözüm her zaman, Uygun C¸özüm Alanının köşe noktalarındadır. Doğru cevap D'dir.
2.Soru
Doğrusal karar modelinin optimum çözümünü bulmak için öncelikle neyin belirlenmesi gerekmektedir?
|
Uygun Çözüm Alanı |
|
Karar Değişkenleri |
|
Uç Nokta Teoremi |
|
Seçenekli çözüm |
|
İçbükey Kümesi |
Bir önceki bölümde görüldüğü gibi, çok farklı alanlardaki problemler doğrusal programlamada, karar modeli olarak modellenebilmektedir. Doğrusal programlama, amaç fonksiyonunu etkileyen kısıtlayıcıların bulunması ve bunların doğrusal eşitlik ve eşitsizlikler olarak verilmesi durumunda, amaca en iyi bir biçimde ulaşılması için, kıt kaynakların en verimli şekilde kullanılmasını sağlayan bir matematiksel yöntemdir. Böyle bir programlama sürecinde, önce gerekli veriler toplanır, probleme ait bir model kurulur ve modelin çözümü araştırılır. Bu çözümler, kurulmuş olan modelin yapısına bağlı olarak tek bir çözüm ya da seçenekli çözüm olabilir. Hatta modelin hiçbir çözümü bulunmayabilir.
Karar modeli açısından her uygun çözüm bir seçenek, Uygun Çözüm Alanı ise seçenekler kümesi anlamındadır. Uygun Çözüm Alanı üzerinde Xj’lere göre, amaç fonksiyonunun maksimum (en büyük) veya minimum (en küçük) değerini aldığı Xj’lere optimum (en iyi) çözüm seti, amaç fonksiyonuna karşı gelen değerine optimum (en iyi) değer denir.
3.Soru
Yukarıda en büyükleme problemi için Simpleks tablosu verilmiştir. 9. ve 10. soruları bu tabloya göre yanıtlandırınız.
Bu problem için amaç fonksiyonun alacağı değer ne olacaktır?
|
10 |
|
15 |
|
125 |
|
135 |
|
150 |
Problem en büyükleme problemi olduğu için amaç fonksiyonu satırındaki tüm değerlerin sıfır ve sıfırdan büyük olması sebebiyle en iyi çözüme ulaşılmıştır. Böylelikle amaç fonksiyonu satırı ve STS sütununun keşistiği yerdeki değer amaç fonksiyonunun aldığı dğeri vermektedir. 125 doğru cevaptır, doğru cevap C'dir.
4.Soru
Bir doğrusal programlama probleminin optimum çözümü, grafik çözüm tekniği ile araştırıldığında, uygun çözüm alanı aşağıdakilerden hangisinde olur?
|
|
|
|
|
|
|
|
|
|
Uygun Çözüm Alanı dışbükey(konveks) bir alandır. Dışbükey alanın temel özelliği, bu alan içinde
iki nokta ele alınıp bir doğru parçasıyla birleştirildiğinde, birleştiren doğru parçasının tamamının alan
kalmasıdır. Doğru cevap A seçeneğidir.
5.Soru
Bir doğrusal programlama modelinin tüm kısıtlarını sağlayan her X vektörüne, ne ad verilir?
|
Seçenekli Çözüm |
|
Uç Nokta |
|
Köşe Nokta |
|
Uygun Çözüm |
|
Karar Modeli |
Bir doğrusal programlama modelinin tüm kısıtlarını sağlayan her X vektörüne, uygun çözüm denir.
Bir önceki bölümde görüldüğü gibi, çok farklı alanlardaki problemler doğrusal programlamada, karar modeli olarak modellenebilmektedir. Doğrusal programlama, amaç fonksiyonunu etkileyen kısıtlayıcıların bulunması ve bunların doğrusal eşitlik ve eşitsizlikler olarak verilmesi durumunda, amaca en iyi bir biçimde ulaşılması için, kıt kaynakların en verimli şekilde kullanılmasını sağlayan bir matematiksel yöntemdir. Böyle bir programlama sürecinde, önce gerekli veriler toplanır, probleme ait bir model kurulur ve modelin çözümü araştırılır. Bu çözümler, kurulmuş olan modelin yapısına bağlı olarak tek bir çözüm ya da seçenekli çözüm olabilir. Hatta modelin hiçbir çözümü bulunmayabilir. Uç(köşe) Nokta Teoremi: Grafik üzerinde Uygun Çözüm Alanının (UÇA) farklı iki noktasının dışbükey birleşimi olarak yazılamayan noktası varsa, buna uç nokta veya köşe nokta denir. Düzlemde bir üçgenin, bir karenin köşeleri uç (köşe) noktadır.
6.Soru
Bir doğrusal karar problemine ait doğrusal bağımsız vektörlerden oluşan, m denklem ve n değişkenin olduğu (mxn’lik ve m<n) bir sistemin çözümünde, m denklem sayısı ve diğer (n-m) tane değişken sıfır değerini almak üzere aşağıdaki ifadelerden hangisi yanlıştır?
|
Sıfırdan farklı değer verilen değişkenlere temel dışı değişken denir. |
|
Değer alması için çözüme alınan değişkenlere temel değişken denir. |
|
Temel dışı değişkenler sıfır iken temel değişkenler için bulunan çözüme temel çözüm denir. |
|
Bir temel çözümde tüm temel değişkenler sıfır veya sıfırdan büyük değer aldıysa bu çözüme bir temel uygun çözüm denir. |
|
Bir temel uygun çözüm aynı zamanda bir uç nokta demektir. |
Doğrusal bağımsız vektörlerden oluşan, m denklem ve n değişkenin olduğu (mxn’lik ve m<n) bir sistemin çözümünde, diğer (n-m) tane değişken sıfır değerini almak üzere, ancak denklem sayısı (m) kadar değişkene değer bulunabilir. Örnek olarak iki denklem ve beş değişkenin olduğu bir sistemde, her seferinde üç değişkene sıfır değerini vererek, iki değişken için çözüm bulunabilir. Burada, sıfır değeri verilen değişkenlere temel dışı, değer alması için çözüme alınan değişkenlere ise temel değişken denir. Temel dışı değişkenler sıfır iken temel değişkenler için bulunan çözüme temel çözüm denir. Bir temel çözümde tüm temel değişkenler sıfır veya sıfırdan büyük değer aldıysa bu çözüme bir temel uygun çözüm denir ve bir temel uygun çözüm aynı zamanda bir uç nokta demektir. Bu nedenle doğru yanıt a) seçeneğidir.
7.Soru
Aşağıdaki fonksiyonlardan hangi(leri)si doğrusal yapıya sahiptir?
|
Yalnız I |
|
Yalnız II |
|
I, II |
|
I, III |
|
II, III |
Aşağıdaki fonksiyonlardan ilk fonksiyon doğrusal yapıya sahiptir,
Doğru cevap C'dir.
8.Soru
Tablo enbüyükleme problemi için verilen Simpleks Tablo'ya aittir. Buna göre kaç kısıt mevcuttur?
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
s1, s2, s3 değerlerinden anlaşılacağı üzere 3 kısıt mevcutttur.
9.Soru
Bir problemin doğrusal programlama modelinin kurulmasında ilk basamak aşağıdakilerden hangisidir?
|
Amaç fonksiyonunun belirlenmesi |
|
Karar değişkeninin tanımlanması |
|
Kısıtlayıcıların belirlenmesi |
|
Üretim planlaması |
|
İşaret kısıtlamasının hazırlanması |
Ekonomide üretim kaynakları veya üretim faktörleri sınırlıdır. Bir işletmenin elindeki makine kapasitesi, teknolojisi, işgücü, enerji, sermaye, hammadde, yarı mamul madde, malzeme gibi üretim faktörleri ile ürünlerine olan talep de sınırlıdır. Dolayısıyla karar değişkenlerinin miktarı da sınırlı olacaktır. Önemli olan, bu kısıtlayıcılar altında amaç fonksiyonunu sağlayan ürünler üretmektir.
10.Soru
Maxz=x1+x2
x1+2x2<=6
2x1+x2<=8
x1,x2>=0 probleminin çözümü sonucu elde edilecek değerler aşağıdakilerden hangisinde verilmiştir?
|
x1=0 x2=4 maxz=4 |
|
x1=4 x2=3 maxz=7 |
|
x1=10/3 x2=4/3 maxz=14/3 |
|
x1=1 x2=5/2 maxz=7/2 |
|
x1=5 x2=4/3 maxz=19/3 |
x1+2x2=6 doğrusu ele alınırsa x1=0 için 2x2=6 x2=3 (0,3) ve x2=0 için x1=6 (6,0) bulunur. Yani bu doğru apsisi (6,0) ve ordinatı (0,3) noktalarında kesmektedir.
2x1+x2=8 doğrusu ele alınırsa x1=0 için x2=8 (0,8) ve x2=0 için 2x1=8 x1=4 (4,0) bulunur. Yani bu doğru apsisi (4,0) ve ordinatı (0,8) noktalarında kesmektedir.
Uygun çözüm alanını bulmak için çizilecek grafik şu şekildedir:
Uygun çözüm alanındaki D noktasını bulmak için iki denklemi taraf tarafa toplayıp x1 ve x2 değerlerini elde etmeye çalışırız. Bunun için ilk denklemi (-2) ile çarpıp ikinci denklemle toplarsak;
(-2)/ x1+2x2=6
2x1+x2=8
Buradan da -3x2=-4 ve x2=4/3 bulunur. İkinci denklemde bu yerine yazılırsa 2x1=20/3 x1=10/3 olarak elde edilir. Yani D noktası (10/3, 4/3)’tür.
Amaç en büyükleme olduğu için orjinden uzaktaki noktalarda çözüm araştırılır. Burada da B, C ve D noktaları için amaç fonksiyonu değerleri karşılaştırılarak en büyük değeri sağlayan nokta optimum çözüm olarak benimsenir.
B(4,0) noktası için maxz=x1+x2=4+0=4
C(0,3) noktası için maxz=x1+x2=0+3=3
D(10/3, 4/3) noktası için maxz=x1+x2=10/3+4/3=14/3 bulunur.
D(10/3, 4/3) noktası için bulunan değer en büyük olduğu için bu nokta optimum olarak kabul edilir.
11.Soru
Doğrusal programlamada optimum çözüm her zaman, Uygun Çözüm Alanının neresindedir?
|
Uç noktalarında |
|
Köşe noktalarında |
|
Merkez noktasıkda |
|
Herhangi bir noktasında |
|
Köşegenlerinin kesişim noktasında |
Doğrusal programlamada optimum çözüm her zaman, Uygun Çözüm Alanının köşe noktalarındadır. Doğru cevap B'dir.
12.Soru
Aşağıdaki işlemlerden hangisi simpleks algoritması için uygun bir işlem değildir?
|
Bir eşitliğin sıfırdan farklı sabit bir sayı ile çarpılması |
|
Bir eşitliğin sıfırdan farklı bir sabit sayıya bölünmesi |
|
Bir eşitliğin herhangi bir katının başka bir eşitliğe eklenmesi |
|
Bir eşitliğin başka bir eşitlik ile çarpılması |
|
Bir eşitliğin herhangi bir katının başka bir eşitlikten çıkarılması |
Simpleks Algoritması’nı uygulayabilmek için verilen denklem sisteminin kısıtlarının eşitlik haline getirilmesi gerekir. Simpleks algoritması ile çözüm aranırken, bir eşitliğin sıfırdan farklı herhangi bir katının başka bir eşitliğe eklemesi ve çıkarılması ile bir eşitliğin sıfırdan farklı bir sabit sayı ile çarpılması ve bölünmesi işlemleri yapılmaktadır. Bir eşitliğin başka bir eşitlik ile çarpılması işlemi yapılamamaktadır.
13.Soru
Aşağıdakilerin hangisinde, doğrusal progrma modeli kurulurken izlenmesi gereken adımları doğru sırada vermektedir?
|
kısıtlayıcıları formüle etme-karar değişkenlerini tanımlama-amaç fonksiyonunu belirleme |
|
amaç fonksiyonunu belirleme-karar değişkenlerini tanımlama-kısıtlayıcıları formüle etme |
|
amaç fonksiyonunu belirleme-kısıtlayıcıları formüle etme-karar değişkenlerini tanımlama |
|
karar değişkenlerini tanımlma-amaç fonksiyonunu belirleme-kısıtlayıcıları formüle etme |
|
kısıtlayıcıları formüle etme-amaç fonksiyonunu belirleme-karar değişkenleri tanımlama- |
Bir problemin, doğrusal programlama modeli kurulurken önce karar değişkenleri tanımlanır, sonrada amaç fonksiyonu ve kısıtlayıcılar formüle edilir.
14.Soru
Verilen doğrusal programlama probleminin optimum çözümü aşağıdakilerden hangisidir?
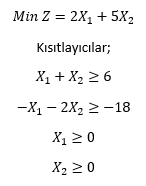
|
|
|
|
|
|
|
|
|
|
15.Soru
I. Bir doğrusal programlama modelinin tüm kısıtlarını sağlayan her X vektörü bir uygun çözümdür.
II. Uygun çözüm alanı dışbükey (konveks) bir alandır.
III. Bir doğrusal programlama modelinin en iyi çözümü varsa, uygun çözüm alanının bir iç noktasıdır.
IV. Farklı iki uygun çözüme ulaşıldığında, bunları birleştiren doğru parçası üzerindeki her bir nokta da bir uygun çözümdür.
Yukarıdaki ifadelerden hangileri grafik çözümün temel esaslarındandır?
|
I, II ve IV |
|
I, III ve IV |
|
I, II ve III |
|
I ve III |
|
II ve III |
Verilen ifadelere bakıldığında, en uygun çözümün bir uç (köşe) nokta olması gerektiğinden grafik çözümün temel esasları I, II ve IV' de doğru olarak verilmiştir.
16.Soru
Maddelerin bir şebeke üzerinde bir noktadan diğerine eniyi (en büyük akışı sağlayacak) şekilde taşınması ile ilgilenen problem hangisidir?
|
En büyük akış. |
|
En kısa yol. |
|
En düşük maliyet. |
|
En küçük örten ağaç. |
|
Rota belirleme |
En büyük akış, maddelerin bir şebeke üzerinde bir noktadan diğerine eniyi (en büyük akışı sağlayacak) şekilde taşınması problemi ile ilgilenir. Su, petrol, gaz vb. maddelerin boru hatlarından taşınması, elektriğin taşınması, haberleşme sistemlerinde bilgi akışının sağlanması ya da kargo işletmelerinde mektupların alıcıya taşınması gibi problemler, bu kapsamda yer almaktadırlar.
17.Soru
AX=b şeklindeki, doğrusal bağımsız vektörlerden oluşan, m denklem ve n değişkenin olduğu (mxn’lik ve m<n) bir sistemin çözümünde sıfır değeri verilen değişkenlere ne ad verilir?
|
Temel Değişken |
|
Temel Dışı Değişken |
|
Uygun Değişken |
|
Çözüm Değişkeni |
|
Uygun Çözüm |
AX=b şeklindeki, doğrusal bağımsız vektörlerden oluşan, m denklem ve n değişkenin olduğu (mxn’lik ve m<n) bir sistemin çözümünde sıfır değeri verilen değişkenlere, temel dışı değişken denir.
18.Soru
Bir yöneylem probleminin karar modeli, kısıtları ve amaç fonksiyonu aşağıda verilmiştir.
Modelin Simpleks Algoritması ile çözülebilmesi için dönüştürülmüş şekli aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
|
Modelde kısıtlar eşitsizlik olarak verilmiştir. Simpleks Algoritması ile çözüm için kısıtlar eşitlik haline dönüştürülmelidir. Birinci kısıt küçük eşitlik, ikinci kısıtta büyük eşitlik olarak verildiğinden çözüm aşağıdaki gibi olur.
19.Soru
Amaç fonksiyonunun en büyükleme olduğu bir problemde simpleks tablodaki x0 satırında aşağıdaki koşullardan hangisi sağlandığında eniyilik koşulları sağlanmış olur.
|
Tüm değerlerin sıfır veya sıfırdan büyük olması |
|
Tüm değerlerin sıfır olması |
|
Tüm değerlerin sıfırdan büyük olması |
|
Tüm değerlerin sıfır veya sıfırdan küçük olması |
|
Tüm değerlerin sıfırdan küçük olması |
Herhangi bir ardıştırmadan sonra tekrar, x0 satırında eniyilik koşullarının sağlanıp sağlanmadığı kontrol edildiğinde, tüm değerlerin sıfır veya sıfırdan büyük olması durumunda, eniyi çözüme ulaşılmıştır ve temele alınması halinde amaç fonksiyonu değerini daha iyiye götürecek bir temel dışı değişken bulunmamaktadır. Bu nedenle doğru yanıt a) seçeneğidir.
20.Soru
Bir doğrusal programlama modelinin grafik çözümünde yapılacak işlemler sırası ile düşünüldüğünde, optimum çözüm noktasının ilan edilmesinden sonra hangi aşama gelmektedir?
|
Optimum çözüm setinin yazılması |
|
Kısıtların her birinin düzlemde bir doğru oluşturması |
|
Modelin tüm kısıtlayıcı fonksiyonlarının aynı koordinat sisteminde çizilmesi |
|
Her bir kısıttın sağlanan bölgelerin taranması |
|
Tüm kısıtları aynı anda sağlayan bölge taranarak “Uygun Çözüm Alanı(UÇA)” nın belirlenmesi |
Uygun Çözüm Alanının köşe noktalarında karar değişkenlerinin ve amaç fonksiyonunun değeri hesaplanarak amacı sağlayan köşe, optimum çözüm noktası olarak ilan edilir. Daha sonra optimum çözüm seti (amaç fonksiyonu ve karar değişkenlerinin değeri) yazılarak çözüme ulaşılmış olur.
-
- 1.SORU ÇÖZÜLMEDİ
- 2.SORU ÇÖZÜLMEDİ
- 3.SORU ÇÖZÜLMEDİ
- 4.SORU ÇÖZÜLMEDİ
- 5.SORU ÇÖZÜLMEDİ
- 6.SORU ÇÖZÜLMEDİ
- 7.SORU ÇÖZÜLMEDİ
- 8.SORU ÇÖZÜLMEDİ
- 9.SORU ÇÖZÜLMEDİ
- 10.SORU ÇÖZÜLMEDİ
- 11.SORU ÇÖZÜLMEDİ
- 12.SORU ÇÖZÜLMEDİ
- 13.SORU ÇÖZÜLMEDİ
- 14.SORU ÇÖZÜLMEDİ
- 15.SORU ÇÖZÜLMEDİ
- 16.SORU ÇÖZÜLMEDİ
- 17.SORU ÇÖZÜLMEDİ
- 18.SORU ÇÖZÜLMEDİ
- 19.SORU ÇÖZÜLMEDİ
- 20.SORU ÇÖZÜLMEDİ


