Genel Matematik Final 33. Deneme Sınavı

Toplam 19 Soru

Diğer "Genel Matematik" Sınavları

PAYLAŞ:

1.Soru

Bir bankadan %1,15 aylık faiz oranı ve 24 ay vade ile 20000 TL tüketici kredisi çekilirse, aylık geri ödeme taksitleri ne kadar olur?

956,6

966,6

976,6

986,6

996,6

2.Soru

işleminin sonucu nedir?

3.Soru

4.Soru

Aşağıda verilen doğru çiftlerinden hangileri kesişen iki doğru belirtmez?

y=2x-1, y=x+3

y=3x-4, y=-2x+1

y=x, y=2x

y=2x+3, y=2x

y=5x-10, y=x

5.Soru

40.000 Türk Lirası yıllık % 25 bileşik faiz oranıyla 2 yıllığına bir bankaya yatırılıyor. Buna göre, 2. yılın sonunda yatırılan para kaç Türk Lirası’na ulaşır?

57.600

58.600

61.000

62.500

65.000

6.Soru

Bir sınıfta öğrenciler sıralara 4’er li otururlarsa 4 öğrenci ayakta kalıyor. 6’şar lı otururlarsa 2 sıra boş kalıyor. Bu sınıfta kaç öğrenci vardır?

36

40

32

42

48

7.Soru

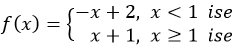fonksiyonunun x₀= 1 noktasındaki limiti için aşağıda söylenenlerden hangisi doğrudur?

Limiti yoktur.

Limiti 1’dir.

Limiti 2’dir.

Limiti 0’dir.

Limiti -1’dir.

8.Soru

h(x) = (x²+1)¹⁰fonksiyonunun türevi nedir?

10(x²+1)⁹

2(x+1)⁹

20x(x²+1)⁹

2x(x²+1)¹⁰

2x(x²+1)⁹

9.Soru

10.Soru

80 sayısını %25 arttırırsak elde edilen sayı aşağıdakilerden hangisidir?

90

100

110

120

85

11.Soru

Bir bankadan %1,5 aylık faiz oranı ve 12 ay vade ile 6000 TL tüketici kredisi çekilirse, aylık geri ödeme taksitleri ne kadar olur?

520,48 TL

530,26 TL

536,84 TL

546,62 TL

548,50 TL

12.Soru

f(x)=x^3+x ve g(x)=2x-1 olmak üzere gof(x) fonksiyonunun türevi aşağıdakilerden hangisidir?

2x^3+2x-1

24x^2-24x+8

3x^2-1

6x^2+2

2x^3+x-4

13.Soru

7

15/2

15

45/2

45

14.Soru

14/3

16/3

100/3

10/3

1/3

15.Soru

Nüfusu 75000000 olan bir ülkenin yıllık nüfus artış yüzdesi %1,2’dir. Buna göre 20 yıl sonra bu ülkenin nüfusu kaç olur?

16.Soru

Bir bankadan %1,35 aylık faiz oranı ve 12 ay vade ile 20000 TL tüketici kredisi çekilirse, borcun amortismanı sonucunda ödenen toplam faiz miktarı kaç TL’dir?

1152

1556

1852

2152

2256

17.Soru

integralinin değeri aşağıdakilerden hangisidir?

ln3

ln2

1

ln(3/2)

ln3-ln2

18.Soru

Mehmet 10000 TL parayı %10 bileşik faiz ile bankaya yatırdığında kaç yıl sonra parası 22000 TL olur?

log 2

log 3

log4

log5

log6

19.Soru