Genel Matematik Final 37. Deneme Sınavı

1.Soru

f 1-1 ve örten bir fonksiyon olmak üzere. Hangisi f(x)=f^(-1) (x) eşitliğini sağlar ?

y=(4-x)/x

y=4/x

2x+4y=1

x + y/4=1

y=(x+4)/x

2.Soru

30000TL aylık %9,25 faiz oranı ile bankaya yatırılıyor. 1 yıl sonra bankada biriken para kaç lira olur?

85 754,25

86 731,85

86 895,26

87224,45

88 652,50

3.Soru

Aşağıdaki noktalardan hangisi x – 3y = 1 doğrusu üzerinde değildir?

(4, 1)

(1, 0)

(2, 3)

(-2, -1)

(7, 2)

4.Soru

f(x)+2g(x)=4x-3 ve f(x)-4g(x)=4x ise f(x)=?

f(x) = 4x-1

f(x) = 4x-2

f(x) = 4x

f(x) = 4x+1

f(x) = 4x-4

5.Soru

Konum fonksiyonu f(t)=15 t^2+7 (metre) olan bir cismin [0,3] saniyelik zaman aralığındaki ortalama hızı ne olur?

25

20

40

45

55

6.Soru

İki bilinmeyenli iki denklemden oluşan bir denklem sistemi için aşağıdaki ifadelerin hangisi doğrudur?

Bu sistemin ikiden fazla çözümü olamaz.

Bu sistemin her zaman tek çözümü vardır.

Bu sistemin eğer iki farklı çözümü varsa, bu ikisinden farklı bir üçüncü çözümü de vardır.

Bu sistemin her zaman çözümü vardır.

Hiç biri.

7.Soru

Bir sayının %8'i ile %24'ünün toplamı 32 ise bu sayı kaçtır?

80

85

90

95

100

8.Soru

Bir evde alanı 24 m² olan bir bölgeye dikdörtgen şeklinde cam yapılacaktır. Bu camın uzun kenarı kısa kenarından 5 metre fazla olduğuna göre uzun kenarın uzunluğu kaç metredir?

9

8

5

4

3

9.Soru

f(x)=x^2-4x+5 fonksiyonunun minimum değeri nedir?

1

2

4

5

8

10.Soru

f,g:R›R , f(x)=x^2 ve g(x)=4x+2 olmak üzere (gof)(3) kaçtır?

14

9

38

36

40

11.Soru

Üç bilinmeyenli bir denklem sitemini çözmek için aşağıdaki işlemlerden hangisi uygulanamaz?

Denklem sistemindeki her bir denkleme aynı sayı eklenebilir

İki denklemin yeri değiştirilebilir

Sistemdeki bir denklem sıfırdan farklı bir sayı ile çarpılabilir

Bir denklem bir sayı ile çarpılıp, sistemdeki diğer bir denkleme eklenebilir

Denklem sistemindeki denklemler ve yok etme yöntemi kullanılarak iki bilinmeyenli doğrusal denklem sistemi elde edilebilir

12.Soru

%14’ü ile %18’inin toplamı 64 olan sayı kaçtır?

160

170

180

190

200

13.Soru

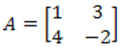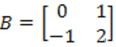vematrisleri için 2A+B matrisi aşağıdakilerden hangisidir?

14.Soru

f(x) = 9-x² ile x ekseni arasında kalan alan kaç br²’dir?

36

0

18

17/3

7/3

15.Soru

olmak üzere a_n=2ⁿ geometrik dizisinin ilk 8 teriminin toplamı kaçtır?

254

255

430

510

1022

16.Soru

Yukarıda verilen üç bilinmeyenli denklem sisteminde x kaçtır?

1

2

x için çözüm yoktur.

x'in sonsuz çözümü vardır.

3

17.Soru

e^2x-e^x-42=0 denkleminin çözümü aşağıdakilerden hangisidir?

ln5

2

ln7

ln8

ln10

18.Soru

4 kilo muz ve 3 kilo kivi 40 lira, 3 kilo muz ve 4 kilo kivi 30 lira ise 2 kilo muz ile 2 kilo kivinin fiyatı kaç liradır?

10

15

20

25

30

19.Soru

f(x)=3x²-6x+1 fonksiyonunun yerel minimum değeri nedir?

2

1

0

-1

-2

20.Soru

3

19/4

19/2

8

19