Matematik 1 Final 16. Deneme Sınavı
Toplam 18 Soru1.Soru
|
(f+g)(x)=0 |
|
(f+g)(x)=2x |
|
Birim fonksiyon |
|
(f+g)(x)=-2x |
|
(f+g)(x)=0 sabit fonksiyonu |
(f+g)(x)=f(x)+g(x)=x-x=0
2.Soru
Bir malın sabit üretim gideri 15000 lira, birim değişken gideri 4 lira ve malın satış fiyatı 16 lira olduğuna başa-baş noktası aşağıdakilerden hangisidir?
|
1250
|
|
1100
|
|
1000
|
|
1125
|
|
900
|
3.Soru
Yukarıdaki şekilde koyu renkle gösterilen 9 elemanının adresi aşağıdakilerden hangisinde doğru olarak verilmiştir?
|
32 |
|
33 |
|
41 |
|
14 |
|
23 |
Matristeki 9 sayısı matrisin üçüncü satırı ve ikinci sütununda bulunuyor. Elemanın indislerle gösterimi olarak adlandırılan bu durum sonucunda, 9 rakamı 32 adresinde yer almaktadır.
4.Soru
|
Reel sayılar |
|
Pozitif reel sayılar |
|
Negatif reel sayılar |
|
Pozitif tamsayılar |
|
Negatif rasyonel sayılar |
f fonksiyonu altında bir a reel sayısı ve -a reel sayısı aynı görüntüye sahip olduklarından, fonksiyonun bire-bir olması için tanım kümesinde mutlak değerleri birbirine eşit olan sayılar bulunmamalıdır.
5.Soru
logx + log6x + log2x = log3x eşitliğini sağlayan x değeri kaçtır?
|
2√2
|
|
√2
|
|
1/√2
|
|
√2/2
|
|
2
|
6.Soru
f(x)=xln(x^2+5) ise f'(-1) aşağıdakilerden hangisidir?
|
3-ln6
|
|
1/3-ln6
|
|
ln6
|
|
1/3
|
|
1/3+ln6
|
7.Soru
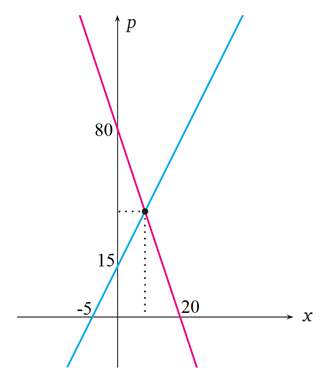 Üstteki arz ve talep doğrularına göre denge noktasının x değeri kaçtır?
Üstteki arz ve talep doğrularına göre denge noktasının x değeri kaçtır?
|
65/7 |
|
60/7 |
|
55/7 |
|
50/7 |
|
45/7 |
Mavi çizgi ile gösterilen denklemde (x1,p1)=(-5,0) ve (x2,p2)=(0,15) olarak yazabiliriz. p=mx+b biçimindeki bir doğrunun eğimi
ile hesaplanır.
ise p=3x+15 olur. Kırmızı çizgi ile gösterilen denklemde (x1,p1)=(20,0) ve (x2,p2)=(0,80) olarak yazabiliriz.
ise p=-4x+80 olur. Her iki denklemde p değerlerini birbirlerine eşitlersek 3x+15=-4x+80 ve x=65/7 olur.
10.Soru
f(x)=x3-3x2+6 fonksiyonun yerel minimum değeri aşağıdakilerden hangisidir?
|
0 |
|
2 |
|
7 |
|
9 |
|
12 |
Önce fonksiyonun türevini alıp kritik noktalarını bulalım. f'(x)=3x2-6x=3x(x-2)'dır. Türevin kökleri x=0 ve x=2'dir. Bu değerleri ikinci türevde yerine yazalım. f''(x)=6x-6'dır.
x=0 için f''(0)=-6<0 olduğundan yerel maksimum noktasıdır.
x=2 için f''(2)=6>0 olduğundan yerel minimum noktasıdır.
11.Soru
olmak üzere
aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
|
dir. İki matrisin eşitliğinden
bulunur. Böylece doğru cevap A seçeneğidir.
12.Soru
Arz ve talep fonksiyonları q=29 + 6p ve q= 150 -5p doğrusal denklem sistemiyle veriliyor. Buna göre (p,q) denge noktası nedir?
|
(0,95) |
|
(100,11) |
|
(95,11) |
|
(90,11) |
|
(11,95) |
Bu denklem sisteminin ortak çözümünden 5q= 145+30p ve 6q= 900-30p olup buradan q=95 bulunur. Bu değer yerine yazılırsa p=11 olarak elde edilir.
13.Soru
Üçüncü dereceden polinomları tarihte ilk çözen bilim adamı aşağıdakilerden hangisidir?
|
Abel |
|
Ferrari |
|
Aristoteles |
|
Thales |
|
Tartaglia |
İkinci dereceden polinomların kökleri bulunduktan sonra matematikçiler üçüncü dereceden polinomlarla uğraşmaya başladılar. Ama bu polinomlar için 16. yüzyıla kadar beklemek gerekti. Bu yüzyılda İtalyan Tartaglia üçüncü dereceden denklemleri çözebildi. Aynı dönemde Ferrari de dördüncü dereceden denklemleri çözmeyi başardı. Bu denklemlerin köklerinin bulunabilmesi için oldukça karışık formüller verdiler.
14.Soru
f(x,y)= (xy-2)3+xy+1 ise f(1,1) aşağıdakilerden hangisine eşittir?
|
-2 |
|
-1 |
|
0 |
|
1 |
|
2 |
x yerine 1, y yerine 1 yazılırsa, f(1,1)=(1.1-2)3+1+1=1 olur.
15.Soru
f(x)=(x2+1)2.lnx ise f'(1) kaçtır?
|
ln2 |
|
e |
|
1 |
|
2 |
|
0 |
Çarpımın türevi kuralından f'(x)=2(x2+1).2x.lnx+(x2+1)2. (1/x) olur.
x=1 değerini bulalım.
f'(1)= 4.1.(1+1).ln1+(1+1).1=2 olarak bulunur.
16.Soru
f(x)=(x+4)?x ise f'(4) aşağıdakilerden hangisidir?
|
4 |
|
2 |
|
1 |
|
0 |
|
-2 |
f'(x)=1•?x+(x+4)•(1/2)x(-1/2)=1•2+(4+4)(1/2)(1/2)=4
-
- 1.SORU ÇÖZÜLMEDİ
- 2.SORU ÇÖZÜLMEDİ
- 3.SORU ÇÖZÜLMEDİ
- 4.SORU ÇÖZÜLMEDİ
- 5.SORU ÇÖZÜLMEDİ
- 6.SORU ÇÖZÜLMEDİ
- 7.SORU ÇÖZÜLMEDİ
- 8.SORU ÇÖZÜLMEDİ
- 9.SORU ÇÖZÜLMEDİ
- 10.SORU ÇÖZÜLMEDİ
- 11.SORU ÇÖZÜLMEDİ
- 12.SORU ÇÖZÜLMEDİ
- 13.SORU ÇÖZÜLMEDİ
- 14.SORU ÇÖZÜLMEDİ
- 15.SORU ÇÖZÜLMEDİ
- 16.SORU ÇÖZÜLMEDİ
- 17.SORU ÇÖZÜLMEDİ
- 18.SORU ÇÖZÜLMEDİ


