Yöneylem Araştırması Ara 1. Deneme Sınavı
Toplam 20 Soru1.Soru
|
x1=2/5 x2=4 Min Z=30 |
|
x1=18/13 x2=20/13 Min Z=140/13 |
|
x1=6 x2=0 Min Z=30 |
|
x1=6 x2=4 Min Z=58 |
|
x1=0 x2=4 Min Z=28 |
Problemin grafik çözümü yukarıdaki şekilde verilmiştir. Buna göre optimum çözüm
şeklinde elde edilir.
2.Soru
Verilen şekillerden hangisi iç bükeydir?
|
Kare |
|
Eşkenar üçgen |
|
Daire dilimi |
|
Bir çeyreği çıkartılmış daire dilimi |
|
Düzgün beşgen |
Çeyreği çıkarılmış daire dilimi içinde seçilecek iki nokta bir doğru parçası ile birleştirildiğinde doğru parçasının bazı noktaları alanın dışında kalabilir. İçbükeydir. Doğru cevap D' dir.
3.Soru
Aşağıda verilen alanlardan hangisi içbükey değildir?
Aşağıda verilen alanlardan hangisi içbükey değildir?
|
|
|
|
|
|
|
|
|
|
Doğru cevap A'dır.
4.Soru
Grafik ve analitik yöntemlerin uygulamadaki güçlüklerini taşımayan, ardışık sayısal çözüm tekniği sınıfındaki yöntem aşağıdakilerden hangisidir?
|
Simpleks Algoritması |
|
Simpleks Algılaması |
|
Simple Algılaması |
|
Simple Algoritması |
|
Study Amphisi |
Simpleks Algoritması, grafik ve analitik yöntemlerin uygulamadaki güçlüklerini taşımayan, ardışık sayısal çözüm tekniği sınıfında bir yöntemdir.
5.Soru
Verilen doğrusal programlama probleminin optimum çözümü aşağıdakilerden hangisidir?
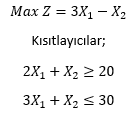
|
|
|
|
|
|
|
|
|
|
6.Soru
Problem çözümünde izlenen yola ne ad verilir?
|
Model |
|
Model kurma |
|
Algoritma |
|
Karar değişkeni |
|
Amaç fonksiyonu |
Model kelime anlamı gerçeğin benzeri demektir. Model kurma, sistemi oluşturan unsurların matematiksel terimlerle ifade edilmesidir. Algoritma, problem çözümünde izlenen yol olarak isimlendirilebilir. Karar değişkeni: bir problemde karar vericinin kontrolü altında olup da, değeri araştırılan eylemler, karar değişkenleridir. Herhangi bir doğrusal programlama probleminde karar verici, karar değişkenlerinin bazı fonksiyonunu maksimum veya minimum yapmak ister. Maksimum veya minimum yapılmak istenen fonksiyona, amaç fonksiyonu adı verilir. Doğru yanıt C’dir.
7.Soru
Uygun çözüm alanı nasıl bir alandır?
|
İçbükey Alanı |
|
Maksimizasyon Modeli |
|
Uç Nokta Teoremi |
|
Dışbükey Alanı |
|
Seçenekli Çözüm |
Doğrusal karar modelinin optimum çözümünü bulmak için öncelikle Uygun Çözüm Alanının(UÇA) belirlenmesi gerekmektedir.
Uç(köşe) Nokta Teoremi: Grafik üzerinde Uygun Çözüm Alanının (UÇA) farklı iki noktasının dışbükey birleşimi olarak yazılamayan noktası varsa, buna uç nokta veya köşe nokta denir. Düzlemde bir üçgenin, bir karenin köşeleri uç (köşe) noktadır.
Uygun Çözüm Alanı dışbükey(konveks) bir alandır. Dışbükey alanın temel özelliği, bu alan içinde iki nokta ele alınıp bir doğru parçasıyla birleştirildiğinde, birleştiren doğru parçasının tamamının alan kalmasıdır. Bir anlamda Uygun Çözüm Alanı kümesindeki herhangi iki nokta çiftini birleştiren doğru parçası, tamamen Uygun Çözüm Alanı kümesinde ise, uygun çözüm alanı dışbükey bir
kümedir. Söz konusu doğru parçasının bir kısmını içine almayan küme ise, içbükey (konkav) kümedir.
Doğrusal programlama, amaç fonksiyonunu etkileyen kısıtlayıcıların bulunması ve bunların doğrusal eşitlik ve eşitsizlikler olarak verilmesi durumunda, amaca en iyi bir biçimde ulaşılması için, kıt kaynakların en verimli şekilde kullanılmasını sağlayan bir
matematiksel yöntemdir. Böyle bir programlama sürecinde, önce gerekli veriler toplanır, probleme ait bir model kurulur ve modelin çözümü araştırılır. Bu çözümler, kurulmuş olan modelin yapısına bağlı olarak tek bir çözüm ya da seçenekli çözüm olabilir.
8.Soru
kısıtının grafiği aşağıdaki grafiklerden hangisinde doğru çizilmiştir?
|
|
|
|
|
|
|
|
|
|
(0,0) noktası denklemde yerine konulduğunda eşitsizliği sağladığı için doğrunun alt kısmı taranır.
9.Soru
Modelin karar değişkenleri Xj’ler, her türlü reel değerleri alabiliyorsa aşağıdaki varsayımlardan hangisi sağlanıyordur?
|
Negatif olmama |
|
Doğrusallık |
|
Bölünebilirlik |
|
Belirlilik |
|
Toplanabilirlik |
Modelin karar değişkenleri Xj’ler, her türlü reel değerleri alabiliyorsa, bölünebilirlik varsayımı sağlanıyor demektir. Böylece, karar değişkenleri, bazı faaliyetlerin düzeyini gösterdiğinden, faaliyetlerin kesirli düzeylerde çalışabileceği varsayılır.
10.Soru
Doğrusal programlama modelinin grafik çözümü aşamaları aşağıdaki maddelerde karışık bir şekilde verilmiştir. Süreç akışına göre sıralandığında, sıralama aşağıdakilerden hangisi gibi olmalıdır?
1. Her bir kısıt eşitlik olarak ele alınıp, karşı gelen doğrunun grafiği çizilerek, kısıtı sağlayan yönü (bölge) işaretlenir.
2. Optimum çözüm seti (amaç fonksiyonu ve karar değişkenlerinin değeri) yazılarak çözüme ulaşılmış olur.
3. Tüm kısıtları aynı anda sağlayan bölge taranarak “Uygun Çözüm Alanı(UÇA)” olarak belirlenir.
4. Uygun Çözüm Alanının köşe noktalarında karar değişkenlerinin ve amaç fonksiyonunun değeri hesaplanarak amacı sağlayan köşe, optimum çözüm noktası olarak ilan edilir.
|
1- 2- 4 - 3 |
|
1- 3 - 2 - 4 |
|
1- 3 - 4 - 2 |
|
1- 2 - 3 - 4 |
|
4- 2 - 3 - 1 |
Grafik çözüm aşamaları göz önüne alındığında; doğru sıralama 1-3-4-2 olacaktır. Doğru cevap C'dıir.
11.Soru
Aşağıdakilerden hangisi doğrusal programlamanın uygulama alanlarından birisi değildir?
|
Sağlık sistemleri |
|
Askeri planlama |
|
Trafik planlaması |
|
Gönüllü hizmetler |
|
Reklam seçimi problemleri |
Doğrusal programlamanın uygulama alanları ile ilgili olarak aşağıdaki liste verilebilir.
-
Ulaştırma ve lojistik problemleri,
-
Endüstriyel üretim planlaması ve envanter (stok) kontrolü
-
Personel programlaması
-
Beslenme(diyet) problemleri
-
Karışım problemleri
-
Tarımsal planlama
-
Finansal planlama
-
Yatırım planlaması
-
Sağlık sistemleri
-
Askeri planlama
-
Trafik planlaması
-
Atama problemleri
-
Reklam seçimi problemleri
-
Karışım problemleri
12.Soru
2 tene doğrusal bağımsız denklem(m=2) ve 9 tane değişkenin(n=9) olduğu AX=b şeklindeki bir denklem sisteminde, bir çözümde kaç temel dışı değişken yer alır?
|
2 |
|
5 |
|
7 |
|
8 |
|
9 |
Doğrusal bağımsız vektörlerden oluşan, m=2 denklem ve n=9 değişkenin olduğu (mxn’lik ve m<n) bir
sistemin çözümünde, diğer (n-m) tane değişken sıfır değerini almak üzere, ancak denklem sayısı (m=2)
kadar değişkene değer bulunabilir. Örnek olarak iki denklem ve dokuz değişkenin olduğu bir sistemde, her
seferinde yedi değişkene sıfır değerini vererek, iki değişken için çözüm bulunabilir. Burada, sıfır değeri
verilen değişkenlere temel dışı, değer alması için çözüme alınan değişkenlere ise temel değişken denir.
13.Soru
Minimizasyonda optimum çözüm için aşağıdaki ifadelerden hangisi doğrudur?
|
Orijinden uzaktır. |
|
Orijine bakılmaz. |
|
Orijinde (0,0) yer alır. |
|
Orijine(0,0) en uzak köşe noktalarında yer alır. |
|
Orijine(0,0) en yakın köşe noktalarında yer alır. |
Minimizasyonda optimum çözüm, orijine(0,0) en yakın köşe noktalarında yer alır.
14.Soru
Sistemi oluşturan unsurların matematiksel terimlerle ifade edilmesi, başka bir deyişle problemlerin matematik diline tercüme edilmesi işlemine ne ad verilir?
|
Fonksiyon oluşturma |
|
Model kurma |
|
Raporlama |
|
Biçimlendirme |
|
Sistem tasarımı |
Soruda tanımı verilen kavram model kurmadır. Doğru cevap B'dir.
15.Soru
Verilen tablo ile aşağıdaki ifadelerden hangisi yanlıştır?
|
Algoritmada en iyi çözüme ulaşılmıştır. |
|
Problemde 2 adet kısıt bulunmaktadır. |
|
Problemin amaç fonksiyonu değeri 125'tir. |
|
x1 ve x2 değişkenlerinin sırasıyla alması gereken değerler 15 ve 10'dur. |
|
Problemde ardıştırma devam etmekte ve temele girmesi gereken değişken s2 değişkenidir. |
Algoritmada en iyi çözüme ulaşılmıştır. Böylelikle E şıkkındaki ardıştırmanın devam etmesi gerektiği bilgisi yanlıştır. Doğru cevap E'dir.
16.Soru
I. Belirlilik
II. Sayılabilirlik
III. Oranlılık
IV. Toplanabilirlik
Yukarıdakilerden hangileri bir karar modelinin doğrusal olabilmesi için gerekli olan özelliklerdendir?
|
Yalnız IV |
|
I, II ve III |
|
I, III ve IV |
|
I, II ve IV |
|
II, III ve IV |
Doğrusal karar modeli geliştirilebilmesi için bazı özellikler vardır: Bunlar; belirlilik, oranlılık, toplanabilirlik ve bölünebilirlik olarak sıralanabilir. Belirlilik, problemde kullanılan parametrelerin değerlerinin bilinmesi, bölünebilirlik, karar değişkenlerinin her reel değeri alabilmesi, oranlılık, karar değişkenlerinin aldıkları değere göre oluşan katkı ve kullanılan kaynak miktarının değişkenin değeri ile doğru orantılı olması, toplanabilirlik ise oluşan katkıların toplanabilmesidir. Bu özellikler var ise bir karar modeli doğrusaldır.
17.Soru
Bir problemde karar vericinin kontrolü altında olup da, değeri araştırılan eylemlere ne ad verilir?
|
Model |
|
Model kurma |
|
Algoritma |
|
Karar değişkeni |
|
Amaç fonksiyonu |
Model kelime anlamı gerçeğin benzeri demektir. Model kurma, sistemi oluşturan unsurların matematiksel terimlerle ifade edilmesidir. Algoritma, problem çözümünde izlenen yol olarak isimlendirilebilir. Bir problemde karar vericinin kontrolü altında olup da, değeri araştırılan eylemler, karar değişkenleridir. Herhangi bir doğrusal programlama probleminde karar verici, karar değişkenlerinin bazı fonksiyonunu maksimum veya minimum yapmak ister. Maksimum veya minimum yapılmak istenen fonksiyona, amaç fonksiyonu adı verilir. Doğru yanıt D’dir.
18.Soru
4 tane doğrusal bağımsız denklem (m=4) ve 6 tane değişkenin (n=6) olduğu Ax=b şeklindeki bir denklem sisteminde bir çözümdeki temel değişken sayısı aşağıdakilerden hangisidir?
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
AX=b şeklindeki, doğrusal bağımsız vektörlerden oluşan, m denklem ve n değişkenin olduğu (mxn’lik ve m<n) bir sistemin çözümünde, diğer (n-m) tane değişken sıfır değerini almak üzere, ancak denklem sayısı (m) kadar değişkene değer bulunabilir. Değer alması için çözüme alınan değişkene temel değişken denir. Böylece 4 bağımsız denklem ve 6 tane değişkenin bulunduğu bu sistemde 6-4=2 değişken sıfır değerini alır. Bu durumda bu denklem sistemindeki temel değişken sayısı 4 olur.
19.Soru
Bir sistemin kendisi yerine onun gibi davranan eşdeğerine ne ad verilir?
|
Model |
|
Problem |
|
Program |
|
Örneklem |
|
Evren |
Bir sistemin kendisi yerine onun gibi davranan eşdeğerine model adı verilir.
20.Soru
Maxz=5x1+3x2
10x1+4x2<=60
2x1+5x2<=20
x1,x2>=0 probleminin çözümü sonucu elde edilecek olan değerler aşağıdakilerden hangisidir?
|
x1=110/21 x2=40/21 maxz=670/21 |
|
x1=0 x2=4 maxz=12 |
|
x1=6 x2=0 maxz=30 |
|
x1=100/21 x2=35/21 maxz=605/21 |
|
x1=6 x2=10 maxz=60 |
10x1+4x2=60 doğrusu ele alınırsa x1=0 için 4x2=60 x2=15 (0,15) ve x2=0 için 10x1=60 x1=6 (6,0) bulunur. Yani bu doğru apsisi (6,0) ve ordinatı ise (0,15) noktalarında kesmektedir.
2x1+5x2=20 doğrusu ele alınırsa x1=0 için 5x2=20 x2=4 (0,4) ve x2=0 için 2x1=20 x1=10 (10,0) bulunur. Yani bu doğru apsisi (10,0) ve ordinatı (0,4) noktalarında keser.
Uygun çözüm alanını bulmak için çizilecek grafik şu şekildedir:Uygun çözüm alanındaki D noktasını bulmak için iki denklemi taraf tarafa toplayıp x1 ve x2 değerlerini elde etmeye çalışırız. Bunun için ikinci denklemi (-5) ile çarpıp ilk denklem ile toplarız.
10x1+4x2=60
(-5)/ 2x1+5x2=20
Buradan da -21x2=-40 x2=40/21 olarak bulunur. Bu değer de ilk denklemde yerine koyulursa 10x1=1100/21 x1=110/21 elde edilir. Yani D noktası (110/21, 40/21)’dir.
Amaç en büyükleme olduğu için orjinden uzaktaki noktalarda çözüm araştırılır. Burada da B, C ve D noktaları için amaç fonksiyonu değerleri karşılaştırılarak en büyük değeri sağlayan nokta optimum çözüm olarak benimsenir.
B(6,0) noktası için maxz=5x1+3x2=5.6+3.0=30
C(0,4) noktası için maxz=5x1+3x2=5.0+3.4=12
D(110/21, 40/21) noktası için maxz=5x1+3x2=5.(110/21)+3.(40/21)=(550/21)+(120/21)=670/21
D(110/21, 40/21) noktası için bulunan değer en büyük olduğu için bu nokta optimum olarak kabul edilir.
-
- 1.SORU ÇÖZÜLMEDİ
- 2.SORU ÇÖZÜLMEDİ
- 3.SORU ÇÖZÜLMEDİ
- 4.SORU ÇÖZÜLMEDİ
- 5.SORU ÇÖZÜLMEDİ
- 6.SORU ÇÖZÜLMEDİ
- 7.SORU ÇÖZÜLMEDİ
- 8.SORU ÇÖZÜLMEDİ
- 9.SORU ÇÖZÜLMEDİ
- 10.SORU ÇÖZÜLMEDİ
- 11.SORU ÇÖZÜLMEDİ
- 12.SORU ÇÖZÜLMEDİ
- 13.SORU ÇÖZÜLMEDİ
- 14.SORU ÇÖZÜLMEDİ
- 15.SORU ÇÖZÜLMEDİ
- 16.SORU ÇÖZÜLMEDİ
- 17.SORU ÇÖZÜLMEDİ
- 18.SORU ÇÖZÜLMEDİ
- 19.SORU ÇÖZÜLMEDİ
- 20.SORU ÇÖZÜLMEDİ


