Matematiksel İktisat Final 11. Deneme Sınavı
Toplam 19 Soru1.Soru
Bir firmanın üretim fonksiyonu olarak verilmiştir. Buna göre firmanın üretimini maksimum yapan istihdam düzeyi nedir?
|
60 |
|
72 |
|
81 |
|
93 |
|
106 |
2.Soru
Bir firmanın üretim fonksiyonu Q(L)=-9L2+468L-900 şeklinde verilmiştir. Buna göre firmanın üretimini maksimum yapan istihdam düzeyi aşağıdakilerden hangisidir?
|
20 |
|
24 |
|
26 |
|
30 |
|
36 |
Fonksiyonun birinci türevi 0’s eşitlenir.
dQ(L)/dL=-18L+468=0
18L-168=0
18L=168
L=26
Fonksiyonun ikinci türevine bakılır.
(d2Q(L)/(dL2 )=-18<0
Fonksiyonun ikinci türevi -18 yani negatif olarak bulunmuştur. Dolayısıyla L=26 üretimi maksimumu yapan istihdam düzeyidir.
3.Soru
I. y=(1/x)+2
II. 2y=4x-7
III. y=15 – 2x
IV. y=(x-2)2
Verilen denklemlerden hangisi ya da hangileri doğrusaldır?
|
Yalnız I |
|
Yalnız II |
|
II ve III |
|
II, III ve IV |
|
I, II ve III |
Bir denklemin doğrusal olması için derecesinin bir olması gerekir. Yani y=ax+b şeklinde yazılabilir olması gerekir. II ve III ‘de yazılmış olan denklem bu şekildedir. I’de yazılmış olan denklem üssel bir denklemdir ve derecesi -1’dir. IV’de ise yazılmış olan denklem bir paraboldür yani karesel bir denklemdir.
4.Soru
Bir kare matrisin sadece köşegen elemanları sıfırdan farklıysa o matrise ne ad verilir?
|
Üçgensel matris |
|
Alt üçgensel matris |
|
Simetrik matris |
|
Köşegen Matris |
|
Matrisin evriği |
Bir kare matrisin sadece köşegen elemanları sıfırdan farklıysa o matrise köşegen matris denir.
5.Soru
olarak verilen üretim fonksiyonunda sermaye ve emeğin kullanım miktarları sırasıyla K=5 ve L=3 ise emeğin marjinal ürünü (MPL) kaçtır?
|
52 |
|
75 |
|
123 |
|
135 |
|
174 |
6.Soru
Yukarıdaki matrisin evriğinde 3. satır 1. sütundaki eleman aşağıdakilerden hangisidir?
|
0 |
|
1 |
|
2 |
|
3 |
|
9 |
Matrisin evriği matrisin satır ve sütunlarının yer değiştirmesidir. Bu durumda 1. satırda yer alan 1,0,3 elemanları sütuna dönüşerek yukarıdan aşağıya doğru konumlanacaktır. Dolayısıyla 3. satır 1. sütündaki eleman 3 olacaktır. Doğru cevap D'dir.
7.Soru
matrisinin determinantı kaçtır?
|
-13 |
|
-9 |
|
9 |
|
13 |
|
27 |
|A|=3(6)-5(1)=18-5=13
8.Soru
I. Marjinal hasıla, toplam hasıla fonksiyonunun türevidir. II. Marjinal maliyet fonksiyonu, toplam maliyet fonksiyonunun türevidir. III. Marjinal fiziki ürün, üretim fonksiyonunun türevi alınarak bulunur. Marjinal fonksiyonlarla ilgili verilen bilgilerden hangisi ya da hangileri doğrudur?
|
Yalnız I |
|
Yalnız II |
|
I ve II |
|
II ve III |
|
I,II ve III |
I. Marjinal hasıla, toplam hasıla fonksiyonunun türevidir. (Doğru)
II. Marjinal maliyet fonksiyonu, toplam maliyet fonksiyonunun türevidir. (Doğru)
III. Marjinal fiziki ürün, üretim fonksiyonunun türevi alınarak bulunur.(Doğru)
Verilen bilgilerin tümü doğru olduğundan Doğru Cevap E seçeneğidir.
9.Soru
I. Eşitlik sayısından daha fazla değişken varsa
II. Eşitlik sayısından daha az değişken varsa
III. Eşitlik sayısı ile değişken sayısı eşitse
Verilenlerden hangisi ya da hangileri bir eşitliği çözüp çözemeyeceğini belirlemek için yeterlidir?
|
Yalnız I |
|
Yalnız II |
|
Yalnız III |
|
I ve II |
|
I ve III |
Eğer eşitlik sayısından daha fazla değişken varsa sistemi çözmek için yeterli ipucunuz yok demektir. Diğer taraftan, eğer elinizde değişkenlerden daha fazla eflitlik varsa, çok fazla ipucunuz var demektir. Eşitlik sayısı ile değişken sayısı eşitse eşitliklerin, doğrusal, bağımsız ve tutarlı olmaları gereklidir. Cevap C şıkkıdır.
10.Soru
x ve y mallarını üreten bir firmanın kar fonksiyonu ise firmanın karını maksimum yapan (x,y) ikilisi aşağıdakilerden hangisidir?
|
(470/23, 2700/23) |
|
(570/23, 2500/23) |
|
(570/29, 2500/29) |
|
(400/17, 1600/17) |
|
(370/19, 1850/19) |
Öncelikle 1. dereceden türevlerin sıfıra eşit olması gerekir. Buna göre:
fx=40-6x+5y=0
fy=50-8y+5x=0
bu denklemlerin ilkini 8'le, ikincisini 5'le çarparsak:
320+40y=48x
250-40y=-25x
bu denklemleri alt alta toplarsak:
570=23x ve x=570/23 olur. Bu değerini herhangi bir denklemde yerine yazdığımızda y=2500/23 olur.
Şimdi 2. derece koşulları da kontrol edip bu değerlerin gerçekten f(x,y) fonksiyonunu maksimum yapıp yapmadığına karar verelim.
2. derece türevleri alırsak:
fxx=-6 fyx=5
fxy=5 fyy=-8
olacaktır. Şimdi de Hessian matrisini oluşturup determinantın pozitif, asal minörlerinin ise negatif olma koşulunu yerine getirip getirmediğine bakalım:
Görüldüğü üzere hem determinantın pozitif olması hem de asal minörlerin negatif olması koşulu yerine getirilmiştir.
11.Soru
A ve B matrisleri eşit olduğuna göre x+y+z toplamı nedir?
|
2 |
|
4 |
|
6 |
|
8 |
|
10 |
2x+3=7
x+y=8
z=-2
buradan x=2, y=6 bulunur.
x+y+z=2+6-2=6
12.Soru
Yıllık nominal faiz oranı %5 ise anaparanızı ikiye katlamak için gereken zaman ne kadardır?
|
15 |
|
13 |
|
14 |
|
20 |
|
10 |
Bu soruyu 70 kuralına göre çözüyoruz. 70 kuralı bize anaparanın ikiye katlanması için gerekli süreyi 70’I faiz oranına bölerek bulmamız gerektiğini söyler. Bu durumda; 70/5=14
13.Soru
I. Sınırlandırılmış Hessian’ın bütün asal minörleri negatifse amaç fonksiyonunun, minimumda olduğunu gösterir.
II. Sınırlandırılmış Hessian’ın asal minörleri pozitiften başlayarak işaret değiştiriyorsa fonksiyonu maksimumdadır.
III. Sınırlandırılmış Hessian’ın bütün asal minörleri negatifse amaç fonksiyonunun, maksimumda olduğunu gösterir.
IV. Sınırlandırılmış Hessian’ın asal minörleri pozitiften başlayarak işaret değiştiriyorsa fonksiyonu minimumdadır.
Verilenlerden hangisi ya da hangileri doğrudur?
|
Yalnız I |
|
Yalnız III |
|
I ve II |
|
III ve IV |
|
Yalnız IV |
Kısıtlı optimizasyon problemlerinde elde edilen sonuçlar her ne kadar amaç fonksiyonunu optimize eden değerleri verse de aslında bulunan noktanın fonksiyonun o kısıt altında bir maksimumda mı yoksa minimumda mı olduğu hakkında bilgi vermez. Bunun için oluşturulan Lagrange fonksiyonunun ikinci dereceden koşullarının incelenmesi gerekmektedir. Bunun için sınırlandırılmış Hessian matrisini oluşturup oluşturulan matrisin negatif mi yoksa pozitif mi belirli olduğunu araştırmak gerekmektedir. Sınırlandırılmış Hessian’ın bütün asal minörleri negatifse amaç fonksiyonunun, minimumda olduğunu gösterir. Sınırlandırılmış Hessian’ın asal minörleri pozitiften başlayarak işaret değiştiriyorsa fonksiyonu maksimumdadır. Yani I ve II önermeleri doğrudur.
14.Soru
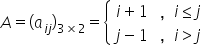 matrisi biçiminde tanımlanmıştır. Buna göre 2A matrisinin evriği aşağıdakilerden hangisidir?
matrisi biçiminde tanımlanmıştır. Buna göre 2A matrisinin evriği aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
|
A matrisinin tanımından;
biçiminde elde edilir. 2A matrisi ise matrisin tüm elemanlarının 2 ile çarpımı sonucunda
olarak bulunur. 2A matrisinin evriği ise matrisin satır elamanları ile sütun elemanlarının (veya sütun elemanları ile satır elemanlarının) yer değiştirmesi ile oluşturulur. Buna göre 2A matrisinin evriği
olup Doğru Cevap B seçeneğidir.
15.Soru
fonksiyonunun
değeri aşağıdakilerden hangisidir?
|
12 |
|
8 |
|
0 |
|
-8 |
|
-12 |
16.Soru
Bir yatırımın 10 yıl sonra iki katı değere ulaşabilmesi için faiz oranı ne olmalıdır?
|
% 6.5 |
|
% 6.8 |
|
% 6.9 |
|
% 7.1 |
|
% 7.18 |
17.Soru
P fiyatı, Q miktarı göstermek üzere buğday üreten bir firma için arz fonksiyonu P = 10Q2 - 15 ve talep fonksiyonu P=2Q2+4Q-3 olarak verilmiştir. Buna göre buğday üreten bu firma için denge miktarı kaç kilogramdır?
|
1kg |
|
1.5kg |
|
2kg |
|
2.5kg |
|
3.5kg |
Denge miktarını bulmak için arz ve talebin birbirine eşit olduğunu noktayı bulmak gerekir. Bunun için arz fonksiyonu ile talep fonksiyonu birbirine eşitlenir. Verilen iki denklemin ortak çözümünden;
10Q2-15=2Q2+4Q-3
8Q2-4Q-12=0
denklemi elde edilir. Denklemi 4 ile sadeleştirirsek 2Q2-Q-3=0 sonucuna ulaşılır. Denklemde a=2, b=-1, c=-3 olduğundan formülleri kullanılarak denklemin köklerinin {-1, 3/2} olduğu anlaşılır. Denklemin köklerini çarpanlara ayırarak da bulabiliriz. Köklere bakıldığında miktar negatif bir değere sahip olamayacağı için bu çözüm olarak kabul edilemez ve 3/2 yani 1.5 değerini kök olarak kabul ederiz. Buna göre buğday üreten bu firmanın denge noktasındaki buğday miktarı 1.5 kilogram olup Doğru Cevap B seçeneğidir.
18.Soru
I. İkinci türev bir fonksiyonun eğiminin azaldığı, arttığı veya sabit kaldığı hakkında bilgi verir. II. İkinci türevi daima pozitif olan fonksiyonlar, dışbükey fonksiyon olarak adlandırılır. III. İkinci türevi daima negatif olan fonksiyonlar, içbükey fonksiyon olarak adlandırılır. İkinci dereceden türev ile ilgili verilenler bilgilerden hangisi ya da hangileri doğrudur?
|
Yalnız I |
|
Yalnız II |
|
I ve II |
|
II ve III |
|
I, II ve III |
I. İkinci türev bir fonksiyonun eğiminin azaldığı, arttığı veya sabit kaldığı hakkında bilgi verir. (Doğru)
II. İkinci türevi daima pozitif olan fonksiyonlar, dışbükey fonksiyon olarak adlandırılır. (Doğru)
III. İkinci türevi daima negatif olan fonksiyonlar, içbükey fonksiyon olarak adlandırılır. (Doğru)
Buna göre Doğru Cevap E seçeneğidir.
19.Soru
Bir fonksiyonun limitinin olması için aşağıdaki şartlardan hangisinin bulunması gereklidir?
|
Sağdan ve soldan limitlerinin mevcut ve birbirine eşit olması gereklidir. |
|
Sağdan veya soldan en az bir yönden limitinin olması yeterlidir. |
|
Sağdan veya soldan en az bir yönden limitinin olması ve limitlerinin birbirine eşit olması gereklidir. |
|
Sağdan veya soldan en az bir yönden limitinin olması yeterlidir. Eğer her iki yönden de limiti var ise sağdaki limitinin soldakinden büyük olması gereklidir. |
|
Sağdan veya soldan en az bir yönden limitinin olması yeterlidir. Eğer her iki yönden de limiti var ise soldaki limitinin sağdakinden büyük olması gereklidir. |
Eğer bir fonksiyonun sağdan ve soldan limitleri mevcut ve birbirine eşit ise bu fonksiyonun limiti vardır denir.
Örneğin:
bu fonksiyonun limiti bulunmamaktadır.
Doğru cevap A'dır.
-
- 1.SORU ÇÖZÜLMEDİ
- 2.SORU ÇÖZÜLMEDİ
- 3.SORU ÇÖZÜLMEDİ
- 4.SORU ÇÖZÜLMEDİ
- 5.SORU ÇÖZÜLMEDİ
- 6.SORU ÇÖZÜLMEDİ
- 7.SORU ÇÖZÜLMEDİ
- 8.SORU ÇÖZÜLMEDİ
- 9.SORU ÇÖZÜLMEDİ
- 10.SORU ÇÖZÜLMEDİ
- 11.SORU ÇÖZÜLMEDİ
- 12.SORU ÇÖZÜLMEDİ
- 13.SORU ÇÖZÜLMEDİ
- 14.SORU ÇÖZÜLMEDİ
- 15.SORU ÇÖZÜLMEDİ
- 16.SORU ÇÖZÜLMEDİ
- 17.SORU ÇÖZÜLMEDİ
- 18.SORU ÇÖZÜLMEDİ
- 19.SORU ÇÖZÜLMEDİ


