Matematiksel İktisat Final 21. Deneme Sınavı
Toplam 19 Soru1.Soru
“y = f (x) fonksiyonu verilmiştir.” Buna göre, x değişkeni a gibi bir değere yaklaşıyorsa y’nin yaklaştığı değer aşağıdakilerden hangisi ile ifade edilir?
|
Limit |
|
Türev |
|
Oran |
|
Trigonometri |
|
Trigonometri |
Limit, bir fonksiyonun bağımsız değişkeni belli bir değere yaklaşırken, fonksiyonun yaklaştığı değeri gösterir. y = f (x) gibi bir fonksiyonu ele alalım. Bu fonksiyonda x değişkeni a gibi bir değere yaklaşırken y’nin yaklaştığı değer limit kavramı ile ifade edilir.
2.Soru
şeklinde yazılmış A ve B matrisleri veriliyor. Buna göre A.B matrisinin elemanlarının toplamı kaça eşittir?
|
30 |
|
31 |
|
32 |
|
21 |
|
20 |
A.B matrisi için a11=(5*1+4*0), a12=(5*2+4*1), a21=(4*1+0*0), a22=(4*2+4*1) terimleri bulunur ve yerine yazılır. Sonuç matrisine eşittir. Bu matrisin elemanlarının toplamı 5+4+14+8=31 sayısıdır.
3.Soru
Bir talep fonksiyonunda fiyatın 210’dan 200’e düşmesi durumuda yay esnekliğinin değerini hesaplayınız.
|
2 |
|
3,4 |
|
210 |
|
5 |
|
0,26 |
P1=210 ve P2=200 verilmiş. Bu fiyat düzeylerinde talep edilen miktarlar:
1000 - 2Q1 = 210
-2Q1 = -790 Q1 = 395
Benzer biçimde fiyatın 210 olması durumunda da Q2 = 400 bulunur.
?P=200-210=-10 ?Q=400-395=5
Doğru cevap E'dir.
4.Soru
şeklinde yazılan, türev ile hesaplanan esneklik ne olarak da adlandıralabilir?
|
Negatif esneklik |
|
Pozitif esneklik |
|
Marjinal teknik ikame oranı |
|
Birim esneklik |
|
Nokta esneklik |
Fiyattaki çok küçük bir değişimin etkisinden bahsettiğimizde, DQ/DP terimini dQ/dP türevi ile değiştirebiliriz. Bu durumda esneklik formülü şu şekilde olacaktır: Bu şekilde hesaplanan esneklik nokta esneklik olarak adlandırılır.
5.Soru
Q = 200 - 3P + Pi + 0,4Y şeklindeki bir talep fonksiyonunda P malın fiyatını, Pi alternatif malın fiyatını ve Y tüketicinin gelirini temsil etmektedir. P=10, Pi=5 ve Y=2000 için talebin fiyat esnekliği aşağıdakilerden hangisidir?
|
0,07 |
|
0,06 |
|
0,05 |
|
0,04 |
|
0,03 |
Öncelikle P=10, Pi=5 ve Y=2000 iken talep edilen miktarı hesaplayalım.
Q = 200 - 3(10) + 1(5) + 0,04(2000) = 975
Fiyat esnekliğini hesaplayabilmek için Q'nun P'ye göre kısmi türevine ihtiyacımız vardır ve bu -3'tür. Buradan;
Doğru cevap E'dir.
6.Soru
Bankaya altı aylık vade ile yıllık %8 nominal faiz oranından 5000 TL yatıran bir müşterinin 3 yıl sonra ne kadar parası olur?
|
6326 |
|
6548 |
|
6875 |
|
7134 |
|
7246 |
Pt=P0(1+r/n)nt
Burada r faiz oranını
n faiz ödemelerinin yılda kaç kez yapıldığını
nt ise faiz ödemelerinin t yılda toplam kaç kez yapılacağını gösterir.
Sorumuz için P0=5000 r=0,08 n=2 t=3
Pt= 5000(1+0,08/2) ^2*3
Pt=5000 (1,04) ^6
Pt= 5000 * 1,2653
Pt=6326
7.Soru
Yukarıda verilen Hessian matrisinin determinantı aşağıdakilerden hangisidir?
|
11 |
|
-11 |
|
49 |
|
-49 |
|
24 |
2x2’lik bir matrisin determinantı aşağıdaki şekilde hesaplanır.
Buna göre yukarıda verilen matrisin determinantı |H|=[(-12)(-5)-(-7)2 ]=60-49=11 olarak bulunur.
8.Soru
Köşegeninin alt veya üstündeki elemanları sıfırdan oluşan kare matrise ne ad verilir?
|
Üçgensel matris |
|
Kofaktör |
|
Matrisin evriği |
|
Vektör |
|
İndis |
Üçgensel matris, köşegeninin alt veya üstündeki elemanları sıfırdan oluşan kare matristir.
9.Soru
Bir fonksiyonun türevi tanımlı olduğu aralıkta sürekli pozitif ise bu fonksiyona ne ad verilir?
|
Azalan fonksiyon |
|
Monoton fonksiyon |
|
Artan fonksiyon |
|
Türevi sıfır fonksiyon |
|
Limitsiz fonksiyon |
Bir fonksiyonun türevi tanımlı olduğu aralıkta sürekli pozitif ise bu fonksiyona artan fonksiyon adı verilir. Bir fonksiyonun türevi tanımlı olduğu aralıkta sürekli azalan ise bu fonksiyona azalan fonksiyon adı verilir. Artan veya azalan fonksiyonlar, genel olarak monoton fonksiyon olarak adlandırılır.
10.Soru
Aşağıda üstel fonksiyonlarla ilgili olarak verilen bilgilerden hangisi yanlıştır?
|
Taban pozitif olduğu sürece fonksiyon daima konveks olacaktır. |
|
Taban pozitif olduğu sürece fonksiyonun görüntü kümesi daima pozitif olacaktır. |
|
Eğer taban 1’den büyük ise bu üstel fonksiyon artan bir fonksiyondur. |
|
Eğer taban 0 ile 1 aralığında (0 ve 1 dahil değil) ise bu üstel fonksiyon azalan bir fonksiyondur. |
|
Eğer taban 1 ise bu üstel fonksiyon önce artan sonra azalan bir fonksiyondur. |
Üstel fonksiyonların grafikleri incelendiğinde fonksiyonun konkavlığı hakkında basit bir kural geliştirilebileceği rahatlıkla izlenebilir. Şöyle ki, üstel fonksiyonlarda taban pozitif olduğu sürece fonksiyon her zaman konveks olacak ve fonksiyonun görüntü kümesi yalnızca pozitif sayılardan oluşacaktır. Eğer taban 1’den büyük ise elimizde artan, yok eğer taban 0 ile 1 aralığında (0 ve 1 dahil değil) ise elimizde azalan bir fonksiyon var demektir. Tabanın 1 olması durumunda fonksiyon sabittir. Doğru cevap E şıkkıdır.
11.Soru
Bireyin fayda fonksiyonu U(X, Y, Z)= 4X + 2Y - X2 - 4Y2+ 10Z - 5Z2 + 30 ise optimum tüketim miktarlarını aşağıdaki üçlülerden hangisidir?
|
X=1, Y=1/4, Z=1/4 |
|
X=1/4, Y=1/4, Z=1 |
|
X=1, Y=1/4, Z=1 |
|
X=2, Y=1/4, Z=1 |
|
X=2, Y=1, Z=1 |
Fayda fonksiyonunun maksimum olduğu noktayı bulmak için X, Y ve Z’ye göre kısmi türevlerini bulup sıfıra eşitlememiz gerekir. ∂U/∂X= 4 - 2X ; ∂U/∂Y= 2 - 8Y ; ∂U/∂Z= 10 - 10Z olarak yazılabilir. Her bir fonksiyonu sıfıra eşitlersek maksimum noktalarını bulabiliriz. 4 - 2X = 0 ise X=2 ve 2 - 8Y = 0 ise Y = 1/4 ve 10 - 10Z = 0 ise Z=1 olarak buluruz. Cevap D seçeneğidir.
12.Soru
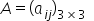 matrisi "i+j toplamının 3 ile bölümünden kalan" ve
matrisi "i+j toplamının 3 ile bölümünden kalan" ve 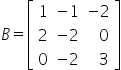 matrisi biçiminde tanımlanıyor. Buna göre A+B matrisi aşağıdakilerden hangisidir?
matrisi biçiminde tanımlanıyor. Buna göre A+B matrisi aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
|
A matrisi "i+j toplamının 3 ile bölümünden kalan" olarak tanımlanmıştır. Bu durumda A matrisini
olarak ifade edebiliriz. A matrisinin indislerinin toplamının 3 ile bölümünün kalanlarından oluşan matris ise
olarak elde edilir. Bu aşamadan sonra B matrisi de verilmiş olduğundan A+B matrisi;
olarak bulunur. Dolayısıyla Doğru Cevap B seçeneğidir.
13.Soru
Sadece x ve y mallarını tüketen bir tüketicinin fayda fonksiyonu U=10x0,4 y0,6 şeklindedir. Buna göre farksızlık eğrisinin eğimi olan Marjinal ikame oranı (MRS) aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
|
14.Soru
Soruda verilen arz ve talep denklemlerine göre ilgili malın denge fiyatı ve miktarı aşağıdakilerden hangisidir?
|
P=10 ; Q=28 |
|
P= 10 ; Q=18 |
|
P= 10 ; Q=38 |
|
P= 8 ; Q=38 |
|
P=11 ; Q=38 |
15.Soru
Bir firma ürettiği mal için 4200 birimlik sipariş almıştır. Firmanın üretim fonksiyonu;
şeklinde verilmiştir.Firma emek (L) için birim başına 2TL. , sermaye (K) için birim başına 8 TL. ödemektedir. Firmanın siparişini en ucuz maliyetle gerçekleştirebilmesi için emek (L) faktöründen kaç birim kullanmalıdır?
|
150 |
|
350 |
|
845 |
|
1250 |
|
1400 |
16.Soru
Fayda fonksiyonu U = 100x1 + 300x2 + 110 olan bir tüketici için x1 ürününden 2, x2 ürününden 1 birim tüketilmesi durumunda elde edilecek fayda ne kadardır?
|
100
|
|
400
|
|
610
|
|
810
|
|
1010
|
17.Soru
fonksiyonunun türevi aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
|
y = [f(x)]k fonksiyonun türevi
y'=kf' (x) [f(x)](k-1)
Buna göre;
f'(x)=5*(-2)*(1-2x)4=-10(1-2x)4
18.Soru
Fayda fonksiyonu U (x, y) = xy şeklinde olan bir tüketici, x malını 12 liradan ve y malını 4 liradan satın almaktadır. Bu iki mal için harcayabileceği toplam bütçesi 600 lira ise bu tüketicinin faydasını maksimize etmesi için optimal tüketim bileşimi aşağıdaki (x,y) ikililerinden hangisinde doğru olarak verilmiştir?
|
(1,10) |
|
(25, 75) |
|
(50, 50) |
|
(75, 25) |
|
(100, 1) |
Öncelikle soruda verilen kısıt ve amaç fonksiyonlarını anlamamız gerekir. Amaç fonksiyonumuz tüketicinin fayda fonksiyonudur, yani U (x, y) = xy. Faydayı, dolayısıyla fayda fonksiyonunu maksimize etmemiz gerekir. Kısıtımız ise elinde olan harcayabildiği bütçesidir, bütçe kısıtıdır. Kısıt fonksiyonunu x, x malının miktarı ve y, y malının miktarı, olarak kabul edersek 12x + 4y = 600 şeklindedir. Soru bu aşamadan sonra herhangi bir kısıtlı optimizasyon problemi gibi çözülebilir. Kısıt fonksiyonundan y = 150 – 3x buluruz ve fayda fonksiyonunda yerine yazarsak U (x, y) = x*(150 – 3x) = 150x – 3x2 olur. Fayda fonksiyonunun türevini alırsak U?(x, y) =150 – 6x denklemini buluruz. Bu denklemi sıfıra eşitlediğimizde x = 25 buluruz. Yerine yazdığımızda y = 75 sonucunu buluruz.
19.Soru
I. Talep eğrisi (doğrusu) pozitif eğimlidir.
II. Arz eğrisi (doğrusu) pozitif eğimlidir.
III. qD talep edilen mal miktarını ve qS arz edilen mal miktarını ifade eder.
IV. Arz ve talep eğrileri aynı yönde eğimlidir.
Arz ve talep denklemleri ile ilgili verilenlerden hangisi ya da hangileri doğrudur?
|
Yalnız I |
|
Yalnız II |
|
I, II ve IV |
|
II ve III |
|
I, II, III ve IV |
I. Talep eğrisi (doğrusu) pozitif eğimlidir. ( Bu ifade yanlıştır. Talep eğrisi (doğrusu) negatif eğimlidir. ) II. Arz eğrisi (doğrusu) pozitif eğimlidir. (Bu ifade doğrudur.) III. qD talep edilen mal miktarını ve qS arz edilen mal miktarını ifade eder. (Bu ifade doğrudur.) IV. Arz ve talep eğrileri aynı yönde eğimlidir. ( Bu ifade yanlıştır. Arz eğrisi pozitif eğimli iken talep eğrisi negatif eğimlidir. )
-
- 1.SORU ÇÖZÜLMEDİ
- 2.SORU ÇÖZÜLMEDİ
- 3.SORU ÇÖZÜLMEDİ
- 4.SORU ÇÖZÜLMEDİ
- 5.SORU ÇÖZÜLMEDİ
- 6.SORU ÇÖZÜLMEDİ
- 7.SORU ÇÖZÜLMEDİ
- 8.SORU ÇÖZÜLMEDİ
- 9.SORU ÇÖZÜLMEDİ
- 10.SORU ÇÖZÜLMEDİ
- 11.SORU ÇÖZÜLMEDİ
- 12.SORU ÇÖZÜLMEDİ
- 13.SORU ÇÖZÜLMEDİ
- 14.SORU ÇÖZÜLMEDİ
- 15.SORU ÇÖZÜLMEDİ
- 16.SORU ÇÖZÜLMEDİ
- 17.SORU ÇÖZÜLMEDİ
- 18.SORU ÇÖZÜLMEDİ
- 19.SORU ÇÖZÜLMEDİ


