Matematiksel İktisat Final 25. Deneme Sınavı
Toplam 17 Soru1.Soru
y=ƒ(x)=ax+b formundaki doğrusal fonksiyonun sıfırdan farklı bir aralık için ortalama değişim oranı fonksiyonun eğimi olarak adlandırılır. Bu değer ilgili fonksiyonda aşağıdakilerden hangisine eşittir?
|
x |
|
a |
|
ax |
|
a+b |
|
ax+b |
y=ƒ(x)=ax+b formundaki doğrusal fonksiyonun sıfırdan farklı bir aralık için ortalama değişim oranı fonksiyonun eğimi olan a'ya eşittir.
Doğrusal bir fonksiyonda ortalama değişim oranı sabittir ve fonksiyonun eğimine eşittir. Doğrusal olmayan bir fonksiyonun ortalama değişim oranı ise sabit değildir. Değişim oranının hesaplandığı aralığa bağlı olarak değişir.
Doğru cevap B'dir.
2.Soru
A matrisinin evriği (A') nin determinantı nedir?
|
-1 |
|
-2 |
|
0 |
|
1 |
|
2 |
Matrisin evriği satır sütunlarının yer değiştirilmesidir.
lA'l=a11a22-a21a12=1.(-2)-0.1=-2-0=-2
3.Soru
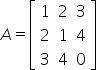matrisi veriliyor. Buna göre 
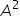matrisinin köşegen elemanlarının aritmetik ortalaması aşağıdakilerden hangisidir?
|
8 |
|
12 |
|
16 |
|
18 |
|
20 |
biçiminde ifade edilir. Buradan
matrisinin köşegen elemanlarını bulmak için ilgili satır ve sütun elemanlarını çarptığımızda köşegen elemanlarının aritmetik ortalamasını;
olarak buluruz. Dolayısıyla Doğru Cevap E seçeneği olur.
4.Soru
Fayda fonksiyonu U = 60x1 + 12x2 + 100 olan bir tüketici için x1 ürününden 0, x2 ürününden 3 birim tüketilmesi durumunda elde edilecek fayda ne kadardır?
|
36
|
|
136
|
|
172
|
|
232
|
|
292
|
5.Soru
Q = 2K2 + 4L2 şeklindeki bir üretim fonksiyonunun homojenlik derecesi aşağıdakilerden hangisidir?
|
6 |
|
5 |
|
4 |
|
3 |
|
2 |
Homojenlik derecesinin bulunması için geliştirilen fonksiyon Euler toremidir.
K(4K) + L(8L) = 4K2 + 8L2 = 2(2K2 + 4L2) = 2Q
Doğru cevap E'dir.
6.Soru
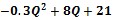biçimindeki karesel kâr fonksiyonunda karı maksimize eden çıktı düzeyi ve maksimum kâr sırasıyla aşağıdakilerden hangisinde doğru olarak verilmiştir?
|
24,10 - 145,67 |
|
13,33 - 74,33 |
|
15,67 - 132,18 |
|
18,16 - 129,12 |
|
10,12 - 120,34 |
Çözüm: Parabolde tepe noktası formülü ile belirlenir. Burada b=8, a= -0.3 değerlerini yerine koyduğumuzda
Tepe noktası=-8/2(-0.3)
=13,33 bulunur. Bu karı maksimize den çıktı düzeyidir. Fonksiyonda bu değeri yerine koyarak maksimum karı elde ederiz:
Maksimum kar= -0.3×13,332 +8×13,33+21
= 74,33
7.Soru
Soruda verilenlere göre denge milli gelir düzeyi aşağıdakilerden hangisidir?
|
100 |
|
140 |
|
180 |
|
240 |
|
350 |
8.Soru
Fayda fonksiyonu U=x0.5y0.5 olan Seda, fiyatları sırasıyla 12 ve 3 Lira olan x ve y mallarından 8 birim fayda elde etmek için ne kadar bütçe ayırmalıdır?
|
48 |
|
96 |
|
144 |
|
192 |
|
240 |
Tüketici Seda verili faydayı minimum harcama yaparak elde etmek isteyeceğinden bu bir minimizasyon problemidir. Sedanın amacı B(x,y)=12x+3y bütçe fonksiyonunu minimum yapmaktır. Bu probleme ilişkin Langrange fonksiyonunu yazalım:
L= 12x+3y+ ?(8- x0.5y0.5)
Şimdi de 1. derece kısmi türevleri sıfıra eşitleyelim:
Lx=12-0.5 ?(y/x)0.5=0 ve buradan 24= ?(y/x)0.5
Ly=3-0.5 ?(x/y)0.5=0 ve buradan 6= ?(y/x)0.5
İçinde ? olan ifadeleri taraf tarafa bölersek:
4=y/x ve buradan y=4x çıkar. Bunu fayda fonksiyonunda kullanırsak:
8= x0.5y0.5
64=xy=x*4x=4x2 ve böylece x=4, y=4x=16 çıkar. Öyleyse gerekli minimum harcama B=12x+3y=(12*4)+(3*16)=96 Liradır. Doğru cevap B'dir.
9.Soru
Bir firmanın sabit maliyeti 4000 TL ve birim başına maliyeti 20 TL olmaktadır. Buna göre Q=200 olduğunda ortalama maliyet aşağıdakilerden hangisine eşit olur?
|
20 |
|
30 |
|
40 |
|
50 |
|
60 |
10.Soru
(a,b) aralığında tanımlı tek değişkenli bir fonksiyonun bu aralıktaki c noktasında birinci türevi sıfır, ikinci türevi -3 ise, f(c) değeri için aşağıdakilerden hangisi geçerlidir?
|
Yerel minimumdur |
|
Yerel maksimumdur |
|
Ortalama değerdir |
|
Büküm noktasıdır |
|
Tanımsızdır |
Fonksiyonun birinci türevi sıfır, ikinci türevi negatif olduğuna göre bu noktada bir yerel maksimum mevcuttur. Yerel minimum için ikinci türevin pozitif, büküm noktası için ise ikinci türevin sıfır olması gerekir.
11.Soru
Hem amaç fonksiyonunun hem de kısıt fonksiyonunun toplam diferansiyelinin alınıp eşanlı olarak çözümlendiği optimizasyon yöntemi aşağıdakilerden hangisidir?
|
Lagrange yöntemi |
|
Toplam diferansiyel yöntemi |
|
Yerine koyma yöntemi |
|
Kısıtsız optimizasyon yöntemi |
|
Sınırlandırılmış Hessian yöntemi |
Amaç fonksiyonunu bir kısıt altında optimize etmenin bir yolu da toplam diferansiyel metodudur. Bu yaklaşımda hem amaç hem de kısıt fonksiyonunun toplam diferansiyeli alınıp eşanlı olarak çözülmesi gerekir.
12.Soru
Soruda verilenlere göre denge milli gelir düzeyi (Y) aşağıdakilerden hangisidir?
|
360 |
|
425 |
|
450 |
|
545 |
|
675 |
13.Soru
yukarıda ve
mallarını kullanan bir tüketicinin fayda fonksiyonu verilmiştir. Buna göre tüketici
malından 100 birim
malından 250 birim tüketiyorsa,
malının marjinal faydası nedir?
|
-450 |
|
-250 |
|
100 |
|
250 |
|
450 |
14.Soru
Bir X malının talep fonksiyonu şu şekildedir:
Bu talep fonksiyonuna göre Q cinsinden yazılmış TR fonksiyonu aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
|
P’yi denklemde çektiğimizde TR=P.Q olduğundan
15.Soru
Q=1000-5P-4Pi+0,02Y
Bir mala ait talep fonksiyonu yukarıda verilmiştir. Q talep miktarını, P malın kendi fiyatını, Pi ikame malın fiyatını ve ise tüketicinin gelir düzeyini ifade etmektedir. P = 10, Pi = 20 Y = 500 olması durumunda talebin gelir esnekliği kaçtır?
|
0,05 |
|
0,09 |
|
0,11 |
|
0,15 |
|
0,20 |
Öncelikle P=10,Pi=20,Y=500 iken talep edilen miktarı hesaplayalım.
Q = 1000-5*10-4*20+0,02*500=880
Talebin gelir esnekliğini hesaplayabilmek için fonksiyonun gelire göre kısmi türevini hesaplamamız gerekmektedir.
?Q/?Y=0,02
Buradan;
EP= Y/Q*?Q/?P = 500/880*(0,02)?0,11
16.Soru
A miktar parayı bir bankaya aylık vade ile yatırıyoruz. 5 yıl sonunda bankada toplam ne kadar paramız olduğunu gösteren formül aşağıdakilerden hangisidir?
|
5 yıl sonundaki para = A(1 + (r/12)) üzeri 60
|
|
5 yıl sonundaki para = A(1 + (r/5)) üzeri 12
|
|
5 yıl sonundaki para = A(1 + (r/12)) üzeri 5
|
|
5 yıl sonundaki para = A(1 + (r/12))
|
|
5 yıl sonundaki para = A üzeri 12
|
17.Soru
U(x,y)=4xy şeklinde yanlız x ve y mallarını tüketen Ahmet'in fayda fonnksiyonu verilmiştir. Ahmet 1 br. x için 3 TL. ve 1 br. y için 5 TL ödemektedir. Bu iki malı tüketmek için Ahmet'in toplam 300 TL. si bulunmaktadır. Buna göre Ahmet maksimum fayda elde edebilmek için ne kadar y tüketmelidir?
|
10 |
|
20 |
|
30 |
|
40 |
|
50 |