MATEMATİK I Dersi POLİNOM FONKSİYONLAR soru cevapları:
Toplam 49 Soru & Cevap#1
SORU:
Birinci dereceden bir polinom ne demektir?
CEVAP:
a≠0 olmak üzere f(x) = ax + b şeklinde ifade edilen fonksiyonlara birinci dereceden bir polinom denmektedir. Bu tür polinomlara doğrusal veya lineer fonksiyonlar da denir. Bu tanımla f(x) = x fonksiyonu da birinci dereceden bir polinom olarak tanımlanabilir.
#2
SORU:
Bir polinomun derecesi ve katsayıları nasıl tanımlanır?
CEVAP:
n negatif olmayan bir tam sayı ve an≠0 olmak üzere a0, a1, a2, …., an gerçel sayıları için f: R→R f(x) = anxn + an-1xn-1 +……+ a2x2 + a1x1 şeklinde ifade edilen f fonksiyonuna n. dereceden polinom fonksiyon denir. Burada a0, a1, a2, …., an sayılarına polinomun katsayıları, an sayısına polinomun baş katsayısı, a0 terimine polinomun sabit terimi ve polinomun içerdiği en büyük kuvvet olan n sayısına da polinomun derecesi denir.
#3
SORU:
Bir polinomun kökü nasıl bulunur?
CEVAP:
f: R→R için f(x) = 0 eşitliğini sağlayan x0 ∈ R sayısına polinomun kökü denmektedir.
#6
SORU:
Birinci dereceden bir bilinmeyenli denklem nedir?
CEVAP:
a, b ∈ R ve a≠0 iken, ax + b = 0 şeklindeki eşitliğe birinci dereceden bir bilinmeyenli denklem denir.
#7
SORU:
Birinci dereceden bir bilinmeyenli bir denklemlerin kökü nasıl bulunur?
CEVAP:
Denklemi sağlayan sayıları bulmak için yapılan işleme denklemi çözmek denir. Denklemin kökü bu denklemi doğrulayan x değeridir. Kök ax + b = 0 olup, x= -b/a yani çözüm kümesi Ç={-b/a} şeklinde yazılır.
#8
SORU:
5(x – 2) + 3 = 5 – x denkleminin çözüm kümesi nedir?
CEVAP:
5x – 10 + 3 = 5 – x
5x – 7 = 5 – x ise 6x = 12
x = 2 ise Ç = {2} olur.
#9
SORU:
İkinci dereceden bir bilinmeyenli denklem nedir?
CEVAP:
a, b, c ∈ R ve a ≠ 0 iken ax2 + bx + c = 0 denklemine bilinmeyeni x olan ikinci dereceden bir bilinmeyenli denklem denir.
#10
SORU:
x2 + 3x - 1 = 0 denkleminin çözüm kümesi nedir?
CEVAP:
a = 1, b = 3 ve c = -1
? = (3)2 – 4 (1) (-1) = 9 + 4 = 13
? < 0 olduğundan Ç = ∅’dir.
#11
SORU:
Matematikte doğrunun tanımı ve özellikleri nedir?
CEVAP:
Aynı doğrultuda yer alan sonsuz çokluktaki noktalar kümesine doğru denir. Sonsuz sayıda noktadan oluşur. İki ucu sınırsızdır. Bir boyutludur yalnız uzunluğu vardır. Eni ve yüksekliği yoktur. Bir noktadan sonsuz sayıda doğru geçer. (Şekil - 1) İki noktadan sadece bir tane doğru geçebilir. (Şekil - 2) Doğru üzerinde sonsuz tane nokta vardır.
#12
SORU:
A = (1, 2) noktasından geçen ve eğimi 3 olan doğrunun denklemi nedir?
CEVAP:
m= y-y1/x-x1
3=y-2/x-1
3x-3=y-2
3x-y-1=0 denklemi bulunur.
#13
SORU:
Parabol nasıl tanımlanır?
CEVAP:
a, b, c ∈ R ve a ≠ 0 olmak üzere, tanımlanan f(x) = ax2 + bx + c biçimindeki fonksiyonlara ikinci dereceden bir değişkenli fonksiyonlar denir.
f = {(x,y) : y = ax2 + bx + c, a, b, c ∈ R ve a ≠ 0}
kümesinin elemanları olan ikililere, analitik düzlemde karşılık gelen noktalara f fonksiyonunun grafiği denir.
İkinci dereceden bir değişkenli fonksiyonların grafiklerinin gösterdiği eğriye parabol denir. f(x) = ax2 + bx + c fonksiyonunun grafiği (parabol), U şeklinde kolları yukarı doğru olan ya da kolları aşağı doğru olan bir eğridir.
#14
SORU:
Parabolün apsisi ve ordinatı neyi ifade eder?
CEVAP:
f: R→R ve f(x) = ax2 + bx + c fonksiyonunun grafiğinin (parabolün);
y eksenini kestiği noktanın; apsisi 0 (sıfır), ordinatı f(0) = c dir. f: R→R ve f(x) = ax2 + bx + c fonksiyonunun grafiğinin (parabolün); y eksenini kestiği noktanın; apsisi 0 (sıfır), ordinatı f(0) = c dir.
x eksenini kestiği noktaların (varsa) ordinatları 0, apsisleri f(x) = 0 denkleminin kökleridir.
#15
SORU:
Kartezyen koordinat düzleminde parabol denklemi ne şekildedir?
CEVAP:
Kartezyen koordinat sisteminde bir parabolün denklemi:
y=ax2+bx+c şeklindedir. Burada a, parabolün yönünü gösterir. Eğer a>0 ise parabolün kolları yukarı doğrudur, eğer a<0 ise aşağı doğrudur. c değeri parabolün y ekseniyle kesiştiği yerdir.
#16
SORU:
Parabol denkleminin diskriminantının alacağı değerlere göre; parabolün Kartezyen düzlemde x ekseniyle olan ilişkisi nedir?
CEVAP:
f: R→R ve f(x) = ax2 + bx + c = 0 denkleminde
?= b2 – 4ac olmak üzere;
? > 0 ise, parabol x eksenini farklı iki noktada keser.
? < 0 ise, parabol x eksenini kesmez.
?= 0 ise, parabol x eksenine teğettir.
#17
SORU:
Parabolün kollarının yukarı veya aşağı yönlü olduğu nasıl belirlenir?
CEVAP:
f: R→R ve f(x) = ax2 + bx + c = 0 denkleminde
a > 0 ise kollar yukarıya doğru,
a < 0 ise kollar aşağıya doğrudur.
#18
SORU:
f(x) = ax2 + bx + c denklemiyle verilen bir parabolün Kartezyen düzlemde grafiğinin çizilebilmesi için yapılması gereken işlemler nelerdir?
CEVAP:
f(x) = ax2 + bx + c fonksiyonunun grafiğini çizmek için sırasıyla aşağıdaki işlemler yapılır:
I. Parabolün eksenleri kestiği noktalar bulunur.
II. Parabolün tepe noktası bulunur.
III. Parabolün kollarının aşağı veya yukarı olma durumuna göre, kesim noktaları ve tepe noktası koordinat düzleminde gösterilip, bu noktalardan geçecek biçimde grafik çizilir.
#19
SORU:
Bir parabolün denklemini yazabilmek için gereken parametreler nelerdir?
CEVAP:
Bir parabolün denklemini tek türlü yazabilmek için, üzerindeki farklı üç noktanın bilinmesi gerekir. (a, b), (m, n) ve (k, t) noktaları y = f(x) parabolü üzerinde ise;
b = f(a), n = f(m), t = f(k) eşitlikleri kullanılarak parabolün denklemi bulunur.
x eksenini x1 ve x2 noktalarında kesen parabolün denklemi, f(x) = a(x – x1)(x – x2) dir.
Tepe noktası T(r, k) olan parabolün denklemi, y = a(x – r)2 + k dir.
#20
SORU:
Eşitsizlik ne demektir, matematikte eşitsizlik kavramı nasıl ifade edilir?
CEVAP:
> (büyüktür), ≥ (büyüktür veya eşittir), < (küçüktür), ≤ (küçüktür veya eşittir) sembolleri ile yazılan matematiksel ifadelere eşitsizlik denir.
#21
SORU:
Büyüktür veya eşittir sembolü neyi ifade eder?
CEVAP:
≥ Büyüktür veya eşittir sembolü. Bu sembolün solundaki ifade sağındakinden büyük de olabilir eşit de olabilir. Örnek: x ≥ 3 ifadesinde x sayısı 3 de olabilir 3'ten büyük de olabilir.
#22
SORU:
Küçüktür veya eşittir sembolü neyi ifade eder?
CEVAP:
≤ Küçüktür veya eşittir sembolü. Bu sembolün solundaki ifade sağındakinden küçük de olabilir eşit de olabilir. Örnek: x ≤ 12 ifadesinde x sayısı 12 de olabilir 12'ten küçük de olabilir.
#23
SORU:
“2 katının 4 fazlası 10'dan küçük olan gerçek sayılar” şeklinde tanımlanan ifadeyi eşitsizlik şeklinde nasıl gösterebiliriz?
CEVAP:
2x + 4 < 10
#24
SORU:
“2 katının 4 fazlası 10'a eşit veya 10'dan büyük olan gerçek sayılar” şeklinde tanımlanan ifadeyi eşitsizlik şeklinde nasıl gösterebiliriz?
CEVAP:
2x + 4 ≥ 10
#25
SORU:
Eşitsizliklerin özellikleri nelerdir?
CEVAP:
Bir eşitsizliğin her iki tarafına aynı sayı eklenir veya her iki taraftan aynı sayı çıkarılırsa eşitsizlik bozulmaz. Bir eşitsizliğin her iki tarafı aynı pozitif sayı ile çarpılır veya aynı negatif sayıya bölünürse eşitsizlik bozulmaz. Bir eşitsizliğin her iki tarafı aynı negatif sayı ile çarpılır veya aynı negatif sayıya bölünürse eşitsizlik yön değiştirir. Eşitsizliğin yön değiştirmesi demek, küçüktür (<) işaretinin büyüktür (>) olması veya büyüktür (>) işaretinin küçüktür (<) işareti olması demektir. Aynı şekilde ≤ işareti ≥ işareti olur ve ≥ işareti ≤ olur.
#26
SORU:
Birinci dereceden bir bilinmeyenli eşitsizlikler nasıl gösterilir?
CEVAP:
a, b ∈ R ve a ≠ 0 olmak üzere,
ax + b > 0
ax + b ≥ 0
ax + b < 0 ve ax + b ≤ 0 biçiminde yazılabilen cebirsel ifadelere, birinci dereceden bir bilinmeyenli eşitsizlik denir.
#27
SORU:
Birinci dereceden bir bilinmeyenli eşitsizliklerin çözüm kümesi nasıl bulunur?
CEVAP:
Eşitsizlikleri çözerken esasında denklemleri çözer gibi çözeriz yani bilinmeyeni eşitsizliğin bir tarafında yalnız bırakırız. Bu durumu oluştururken de yukarıda öğrendiğimiz özellikleri kullanırız. Birinci derece denklemlerin çözüm kümesinde bir sayı bulunurken birinci dereceden bir bilinmeyenli eşitsizliklerin çözüm kümesi ise bir sayı değil bir aralıktır. Eşitsizliğin çözüm kümesini sayı doğrusunda gösterirken “≤ veya ≥” sembollerinde başlangıç noktasının içi dolu, “< veya >” sembollerinde başlangıç noktası çözüm kümesine dahil olmadığından içi boş olur.
#28
SORU:
2x + 3 > 11 eşitsizliğinin çözüm kümesi nedir?
CEVAP:
X'i yalnız bırakmak için önce her iki taraftan 3 çıkartılır.
2x + 3 − 3 > 11 − 3
2x > 8
her iki taraf 2'ye bölünür.
x > 4
Denklemin çözüm kümesi Ç = { x | x > 4 , x ∈ R
#29
SORU:
40 − x ≤ 50 eşitsizliğinin çözüm kümesi nedir?
CEVAP:
40 − x − 40 ≤ 50 − 40 − x ≤ 10 eşitsizliğin her iki tarafı −1 ile çarpılır.
Negatif sayı ile çarptığımız için aradaki işaretin yön değiştirdiğini unutmamalıyız.
− x . − 1 ≤ 10 . − 1
x ≥ −10
Denklemin çözüm kümesi Ç = { x | x ≥ 10 , x ∈ R } olarak bulunur.
#30
SORU:
"Polinom" kelimesinin anlamı nedir?
CEVAP:
"Poli" Latincede çok anlamına gelmektedir. "Nom" ise terim anlamına gelir. Yani Polinom çok terimli anlamına gelir.
#31
SORU:
Birinci derece polinomların diğer isimleri nelerdir?
CEVAP:
Bu tür polinomlara doğrusal ya da lineer fonksiyonlar da denir.
#32
SORU:
a, b, c gerçel sayılar ve a ?0 olmak üzere f(x) = ax²+bx+c şeklindeki fonksiyonun derecesi kaçtır?
CEVAP:
Bu şekilde ifade edilen fonksiyona ikinci dereceden polinom denir.
#33
SORU:
f(x)= ax²+ bx+ c = bx+ c olursa a'nın değeri kaçtır?
CEVAP:
a= 0 olursa f(x)=ax²+bx+c=bx+c olur.
#34
SORU:
İkinci dereceden polinomların diğer adı nedir?
CEVAP:
İkinci dereceden polinomlara kuadratik fonksiyon da denir.
#35
SORU:
Sabit fonksiyonların derecesi kaçtır?
CEVAP:
Sabit fonksiyonların derecesi 0(sıfır)'dır.
#36
SORU:
Baş katsayısı 1 olan polinoma ne ad verilir?
CEVAP:
Baş katsayısı 1 olan polinoma monik polinom denir.
#38
SORU:
(x+y)2 = x2+ 2xy+ y2 Bu eşitlikte x ve y sayılarının yerine hangi sayıyı koyarsanız koyun yine bu eşitliği verecektir. Bu tür eşitliklere ne denir?
CEVAP:
Bu tür eşitliklere özdeşlik denir.
#39
SORU:
ax2 + bx+ c polinomu için 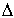 = b2- 4ac < 0 ise kök nedir?
= b2- 4ac < 0 ise kök nedir?
CEVAP:
Bu durumda kök yoktur.
#41
SORU:
Altın oran nedir?
CEVAP:
Bir ipi öyle bir yerden keselim mi, böldüğümüzde oluşan ip parçalarından büyük olanın uzunluğunun küçük olanın uzunluğuna oranı, ipin tamamının uzunluğunun büyük parçanın uzunluğuna oranına eşit olsun. Buna altın oran denir.
#42
SORU:
Altın oranı hangi denklemle gösterebilirsiniz?
CEVAP:
a/b= a+b/a yani a/b=1+ b/a olmalıdır. O halde aradığımız orana x=a/b dersek, aradığımız sayı x= 1+ 1/x eşitliğini sağlayan pozitif x sayıdır. Bu denklemi biraz düzenlersek altın oran x= x+1/x yani x2= x+1 eşitliğini sağlayan pozitif sayıdır.
#43
SORU:
x1 ? x2 olmak üzere, düzlemde (x1, y1) ve (x2, y2) noktalarından geçen doğrunun denklemi nedir?
CEVAP:
y- y1/ x- x1 = y2 - y1/ x2 - x1
#44
SORU:
Eğimi a olan ve (x1, y1) noktasından geçen doğrunun denklemi nedir?
CEVAP:
y- y1 = a(x- x1)
#46
SORU:
Bütün noktaları ortak olan iki doğruya ne denir?
CEVAP:
Bütün noktaları ortak olan iki doğruya çakışık doğru denir.
#47
SORU:
Parabolun tanımı nedir?
CEVAP:
Düzlemde, sabit bir nokta ve sabit bir doğruya eşit uzaklıktaki noktaların kümesine parabol denir. Bu sabit noktaya parabolün odak noktası, doğruya da doğrultmanı denir.
#48
SORU:
Bir parabol, odaktan geçen ve doğrultmana dik olan bir doğruya göre hangi konumdadır?
CEVAP:
Bir parabol, odaktan geçen ve doğrultmana dik olan doğruya göre simetriktir, bu doğruya simetri ekseni de denir.
#49
SORU:
Bir eşitsizlikte, eşitsizliği değiştiren ve değiştirmeyen işlemler nelerdir?
CEVAP:
Bir eşitsizlikte, eşitsizliğin her iki tarafına aynı sayının eklenmesi veya çıkartılması eşitsizliği değiştirmez. Bir eşitsizlikte, eşitsizliğin her iki tarafının aynı pozitif sayıyla çarpılması veya bölünmesi eşitsizliği değiştirmez. Ama eşitsizliğin her iki tarafının negatif bir sayıyla çarpılması veya bölünmesi eşitsizliğin yönünü değiştirir.


