Matematiksel İktisat Final 6. Deneme Sınavı
Toplam 20 Soru1.Soru
Bir ekonomide tüketim fonksiyonu C=56+0.72Y olarak tanımlanmıştır. Buna bu ekonomideki marjinal tasarruf eğilimi (MPS) aşağıdakilerden hangisidir?
|
0.36 |
|
0.44 |
|
0.56 |
|
0.72 |
|
0.28 |
Marjinal tüketim eğilimi (MPC) tüketim fonksiyonunun eğimidir. Bir fonksiyonun eğimi ise fonksiyonun birinci türevi alınarak bulunur. Buna göre; Marjinal tasarruf eğilimi 0.72 olarak bulunmuştur. Marjinal tasarruf eğilimi ile marjinal tasarruf eğiliminin toplamı 1’e eşit olacağından.
Marjinal tasarruf eğilimi 0.28 olarak bulunmuştur.
2.Soru
ln2=0.7 olduğunu varsayarsak f(x)=xx fonksiyonunun x=2'deki türevi kaça eşittir?
|
0.7 |
|
1.7 |
|
6.2 |
|
6.8 |
|
7.1 |
Logaritmik türev alma kurallarını kullanarak çözüme ulaşmak gerekmektedir. Buna göre f'(x)=(ln(x)+1)xx şeklinde elde edilir.
x=2 olduğunda f'(2)=(ln(2)+1)22 olur. ln(2) = 0.7 kabul edildiğine göre f'(2)=(0.7 + 1)*4 = (1.7)*4 = 6.8 sonucu bulunur.
3.Soru
fonksiyonunun yerel minimum ve yerel maksimum değerleri aşağıdaki ikililerden hangisidir?
|
(1,3) |
|
(2,3) |
|
(2,6) |
|
(3,6) |
|
(6,12) |
İlk önce fonksiyonun birinci türevi alınır.
f'(x) = 3x2 + 24x + 36'dır.
Kritik değerleri elde etmek için türev fonksiyonu sıfıra eşitlenir.
3x2 + 24x + 36 = 0
Denklemi çarpanlarına ayırarak iki kritik değer bulunur.
x1 = 2 (bu noktada f'(2) = 0 ve f(2) = 40 olur)
x2 = 6 (bu noktada f'(6) = 0 ve f(6)= 8 olur)
Doğru cevap C'dir.
4.Soru
Şekilde gösterilen grafiklerin eğimleri aşağıdakilerden hangileri olabilir?
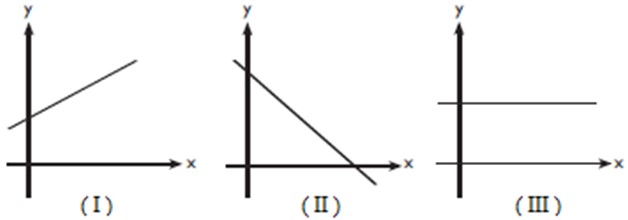
|
I. eğim = 0, II. eğim = 2, III. eğim = 2 |
|
I. eğim = 5, II. eğim = (-3), III. eğim = 0 |
|
I. eğim = (-3), II. eğim = (-3), III. eğim = 0 |
|
I. eğim = (-3), II. eğim = 5, III. eğim = 0 |
|
I. eğim = 2, II. eğim = 2, III. eğim = 0 |
Bir fonksiyonun eğimi artış ya da azalışını anlamak için önemlidir. Eğiminin pozitif yani sıfırdan büyük olduğu durumda fonksiyon artış göstermektedir. Bu bir değerin kendinden önceki değerden daha fazla olduğu anlamına gelir. Eğimi pozitif olan bir doğru sağa yukarı yöne meyilli olur ve eğiminin değeri arttıkça doğru da dikleşir. Eğiminin negatif yani sıfırdan küçük olduğu durumda fonksiyon azalış göstermektedir. Bu yüzden bir değeri kendinden önceki değerinden daha az olduğu anlamına gelir. Eğimi negatif olan bir doğru sağa aşağı yöne meyilli olur. Eğimin sıfır olması durumunda ise tüm değerler sabittir ve x eksenine paralel olur. Bu bilgilere göre seçenekler incelendiğinde B seçeneğindeki I. eğimin pozitif yani 5, II. eğimin negatif yani (-3) ve III. eğimin 0 olduğu söylenebilir. Bu nedenle Doğru Cevap B seçeneği olur.
5.Soru
Bugün bankaya yatırılan 10.000 TL paranın 6 yılın sonunda 20.000 TL olabilmesi için faiz oranı yaklaşık kaç olmalıdır?
|
%10 |
|
%12 |
|
%15 |
|
%17 |
|
%20 |
Pt=P0(1+r)t
20.000=10.000 (1+r)6
20.000/10.000=(1+r)^6
2=(1+r)^6
2^1/6=1+r
1,1224=1+r
r=0,1224 Faiz oranı yaklaşık %12 olmalıdır.
6.Soru
değeri aşağıdakilerden hangisine eşittir?
|
1 |
|
0 |
|
-1 |
|
|
|
e |
Her sayının sıfırıncı kuvveti 1 dir.
7.Soru
Aşağıdakilerden hangisi A malının taleb fiyatının esnek olduğunu gösterir?
|
0 |
|
-1/2 |
|
5 |
|
1 |
|
-5/2 |
Talebin fiyat esnekliği 0 ve -1 aralığında ise o mal esnek olmayan mal; eğer fiyat esnekliği -1 den -sonsuz aralığında ise o mal esnek maldır.
8.Soru
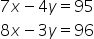 denklem sistemini sağlayan (x, y) değerleri aşağıdakilerden hangisidir?
denklem sistemini sağlayan (x, y) değerleri aşağıdakilerden hangisidir?
|
(9, -8) |
|
(8, -9) |
|
(-9, 8) |
|
(-8, 9) |
|
(-9, -8) |
Verilen lineer denklem sistemini;
matrisleri yardımıyla ifade edebiliriz. Buradan Cramer Kuralı yardımıyla x ve y değerlerini
olarak buluruz. Bu nedenle Doğru Cevap A seçeneği olur.
9.Soru
ve
matrisleri verilmiştir. A.B matrisi aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
|
10.Soru
Aşağıdaki denklemlerden hangisi doğrusaldır?
|
y=3+5x2 |
|
y=4+6x3 |
|
y=x+xy2 |
|
y=5x4 |
|
y=2+3x |
Bir eşitliğin doğrusal olması, kontrol edilen bütün eşitliklerin, y=a+bx formatında olması gerekliliğidir. Bu özellik formattaki a veya b'nin 0 ya da 1 olduğu durumları da içerir ki böyle durumlarda y=a ya da y=x olur. Doğrusal olması üssün, kare, küp ......., kök, xy ve x/y olmaması durumunu ifade eder. Bu tanıma uyan sadece E seçeneğindeki denklemdir.
11.Soru
Q = 250 - 4P - 2Pi - 0,2Y şeklindeki bir talep fonksiyonunda P malın fiyatını, Pi alternatif malın fiyatını ve Y tüketicinin gelirini temsil etmektedir. P=10, Pi=30 ve Y=1000 için çapraz fiyat esnekliği aşağıdakilerden hangisidir?
|
0,17 |
|
0,19 |
|
0,21 |
|
0,23 |
|
0,25 |
Öncelikle P=10, Pi=30 ve Y=1000 iken talep edilen miktarı hesaplayalım.
Q = 250 - 4(10) - 2(30) - 0,2(1000) = 350
Çapraz fiyat esnekliğini bulmak için öncelikle fonksiyonun alternatif malın fiyatına göre kısmi türevini hesaplarız ve bu -2'dir. Buradan;
Doğru cevap A'dır.
12.Soru
Bir malın talebi sadece fiyatının değil gelirin (I) de bir fonksiyonu olarak aşağıdaki gibi verilmiştir.
Qd=-2P+40+I
Arz fonksiyonu ise Qs=3P-10 şeklindedir. Eğer gelir I=40 ise denge fiyatı aşağıdakilerden hangisidir?
|
15 |
|
18 |
|
24 |
|
30 |
|
35 |
Qd=-2P+40+I
Qs=3P-10
Denge koşulu Qd=Qs sağlanmalıdır.
-2P+40+I=3P-10
40+10+I=5P
50+I=5P
P=10+I/5
Gelirin 40 olması durumunda
P=10+40/5
P=18 olur.
13.Soru
Aşağıdakilerden hangisi piyasada veri bir zamanda bir malın talep edilen miktarını etkileyen faktörlerden biri değildir?
|
Malın cinsi |
|
Tüketicilerin gelirleri |
|
İlgili malların fiyatlarındaki değişmeler |
|
Tüketicilerin zevk ve tercihleri |
|
Tüketicilerin beklentileri |
Piyasada veri bir zamanda bir malın talep edilen miktarını O malın fiyatı, Tüketicilerin gelirleri, İlgili malların fiyatlarındaki değişmeler, Tüketicilerin zevk ve tercihleri, Tüketicilerin beklentileri gibi pek çok faktör etkiler.
14.Soru
P=75-5Q şeklindeki bir talep fonksiyonunda, p=10 olduğunda talep esnekliği aşağıdakilerden hangisidir?
|
0,086 |
|
0,86 |
|
1,08 |
|
1,86 |
|
1,95 |
Q=25-1/5.P Q=25-1/5.10=23
Q'=-1/5 Esneklik formülünden;
15.Soru
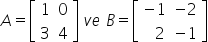 matrisleri tanımlanıyor. Buna göre A-B matrisinin iz değeri aşağıdakilerden hangisidir?
matrisleri tanımlanıyor. Buna göre A-B matrisinin iz değeri aşağıdakilerden hangisidir?
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
Verilen A ve B matrisleri yardımıyla A-B matrisi
biçiminde elde edilir. A-B matrisinin iz değeri buradan
olarak bulunur. Bu nedenle Doğru Cevap E seçeneğidir.
16.Soru
yukarıda ve
mallarını kullanan bir tüketicinin fayda fonksiyonu verilmiştir. Buna göre tüketici
malından 100 birim
malından 250 birim tüketiyorsa,
malının marjinal faydası nedir?
|
50 |
|
100 |
|
285 |
|
300 |
|
325 |
17.Soru
I. ln (y) fonksiyonu yalnızca y < 0 olduğu yerlerde tanımlıdır.
II. ln(y) fonksiyonu sürekli artan ve konkav bir fonksiyondur.
III. ln(e) = 0
IV. Doğal tabanlı üstel fonksiyon tanımlı olduğu her yerde sürekli konveksdir.
V. Doğal logaritmik fonksiyon sürekli konkavdır.
Logaritmik fonksiyonlar ve üstel fonksiyonlarla ilgili verilenlerden hangisi ya da hangileri doğrudur?
|
Yalnız I |
|
II, III ve IV |
|
II, IV ve V |
|
I, II ve III |
|
II ve III |
I. ln (y) fonksiyonu yalnızca y < 0 olduğu yerlerde tanımlıdır. (Bu tanım yanlıştır. ln (y) fonksiyonu yalnızca y > 0 olduğu yerlerde tanımlıdır.) II. ln(y) fonksiyonu sürekli artan ve konkav bir fonksiyondur. (Bu tanım doğrudur.) III. ln(e) = 0 (Bu tanım yanlıştır. ln(1)=0) IV. Doğal tabanlı üstel fonksiyon tanımlı olduğu her yerde sürekli konveksdir. (Bu tanım doğrudur.) V. Doğal logaritmik fonksiyon sürekli konkavdır. (Bu tanım doğrudur.)
18.Soru
TC toplam maliyeti, MP marjinal fiziki ürünü, P faktör fiyatını, K ve L ise sırasıyla sermaye ve emeği göstermek üzere verili üretim fonksiyonunu esas alıp maliyet minimizasyonu yapan bir firma için denge halinde aşağıdakilerden hangisi geçerlidir?
|
|
|
|
|
|
|
|
|
|
İster maliyet minimizasyonu olsun ister ürün miktarı maksimizasyonu, denge halinde her bir üretim faktörü için marjinal fiziki ürünün o faktörün fiyatına oranı eşit olmalıdır. Aksi halde fiyatına nazaran marjinal fiziki ürünü daha yüksek olan faktör daha fazla kullanılacaktır.
19.Soru
İki mal üreten bir firma için toplam hasıla fonksiyonu TR(Q1, Q2) = -5Q12 - 3Q1Q2 + 23Q1 + 3Q22 + 20 olduğuna göre firmanın toplam hasıla minimum yapan üretim değerleri nedir?
|
Q2 = 1 ve Q1 =1 |
|
Q2 = 2 ve Q1 = 1 |
|
Q2 = 1 ve Q1 =2 |
|
Q2 = 2 ve Q1 =2 |
|
Q2 = 3 ve Q1 =2 |
İlk önce TR’nin Q1 ve Q2’e göre birinci mertebeden kısmi türevi bulunur. ?TR/?Q1 = -10Q1 - 3Q2 + 23 ve ?TR/?Q2 =-3Q1 + 6Q2 bulunur, bu iki denklemi sıfıra eşitlediğimizde -10Q1 - 3Q2 + 23 = 0 ve -3Q1+6Q2=0 eşitliğini elde ederiz. İkinci fonksiyon için 3Q1=6Q2 buradan Q1=2Q2 eşitliğini buluruz. Bu eşitliği ilk fonksiyonda yerine yazdığımızda ise -20Q2 - 3Q2 + 23 = 0 eşitliğini buluruz. Bu eşitliği çözdüğümüzde -23Q2 = - 23 Buradan Q2 = 1 ve Q1 =2 sonucunu elde ederiz. Cevap C şıkkıdır.
20.Soru
Bir firmanın ortalama maliyet fonksiyonu AC(Q) = 2Q2 - 40Q + 65 şeklindedir. Buna göre firmanın ortalama maliyetini minimum yapan üretim düzeyi aşağıdakilerden hangisidir?
|
2 |
|
4 |
|
6 |
|
8 |
|
10 |
Ortalama maliyet fonksiyonunun sıfıra eşitlendiği noktadaki üretim düzeyi ortalama maliyeti sıfır yapan düzeydir.
4Q = 40
Q = 10
Ortalama maliyeti minimum yapan üretim düzeyi 10 birimdir. Doğru cevap E'dir.
-
- 1.SORU ÇÖZÜLMEDİ
- 2.SORU ÇÖZÜLMEDİ
- 3.SORU ÇÖZÜLMEDİ
- 4.SORU ÇÖZÜLMEDİ
- 5.SORU ÇÖZÜLMEDİ
- 6.SORU ÇÖZÜLMEDİ
- 7.SORU ÇÖZÜLMEDİ
- 8.SORU ÇÖZÜLMEDİ
- 9.SORU ÇÖZÜLMEDİ
- 10.SORU ÇÖZÜLMEDİ
- 11.SORU ÇÖZÜLMEDİ
- 12.SORU ÇÖZÜLMEDİ
- 13.SORU ÇÖZÜLMEDİ
- 14.SORU ÇÖZÜLMEDİ
- 15.SORU ÇÖZÜLMEDİ
- 16.SORU ÇÖZÜLMEDİ
- 17.SORU ÇÖZÜLMEDİ
- 18.SORU ÇÖZÜLMEDİ
- 19.SORU ÇÖZÜLMEDİ
- 20.SORU ÇÖZÜLMEDİ


