Matematiksel İktisat Final 15. Deneme Sınavı
Toplam 19 Soru1.Soru
Bir mal için talep edilen miktarın, fiyatın doğrusal bir fonksiyonu olduğunu varsayalım. Fiyat (P) 5 iken talep edilen miktar (Q) 300 birim ise ve fiyat 10’a çıktığında talep edilen miktar 100 birime düşüyorsa, doğrusal talep fonksiyonu aşağıdakilerden hangisidir?
|
Q=-40P+500 |
|
Q=-20P+600 |
|
Q=-5P+250 |
|
Q=-8P+300 |
|
Q=-4P+100 |
Fiyatlar (P1,P2)=(5,10)
Miktarlar (Q1,Q2)=(300,100) olarak verilmiştir.
Doğru denklemini belirlemek için nokta nokta formülünü kullanabiliriz.
doğrunun eğimi a=y2-y1/x2-x1 formülü ile bulunur
Talep eşitliğine uyarlarsak eğim a=Q2-Q1/P2-P1 formülü ile bulunabilir.
a=100-300/10-5 buradan a=-200/5 a=-40 bulunur. Talep eşitliğinin eğimi -40'tır.
Doğru denklemini belirlemek için de nokta eğim formülünü kullanabiliriz.
y-y1=a(x-x1)
Q-Q1=a(P-P1)
Q-300=-40(P-5)
Q-300=-40P+200
Q=-40P+500 bulunur.
2.Soru
Bir kişi X ve Y mallarını tüketmektedir. Bu malların tüketiminden elde ettiği faydayı gösteren fonksiyon, olarak verilmiştir.Buna göre, bu kişinin faydasını maksimum kılması için X malından ne kadar tüketmesi gerekir?
|
1/2 |
|
3/2 |
|
5/2 |
|
2/3 |
|
2/5 |
3.Soru
Sadece köşegen elemanları sıfır olmayan matris aşağıdakilerden hangisidir?
|
Köşegen Matris |
|
Üçgensel Matris |
|
Birim Matris |
|
Skaler Matris |
|
Kare Matris |
Satır ve sütun sayısı birbirine eşit olan matrise kare matris, köşegeninin alt veya üstündeki elemanları sıfırdan oluşan kare matrise üçgensel matris, eğer bir köşegen matrisin köşegen elemanları birbirine eşitse o matrise skaler matris, köşegen elemanları bire diğer tüm elemanları sıfıra eşit olan matrise birim matris denir. Sadece köşegen elemanları sıfır olmayan matrise ise Köşegen Matris denmektedir. Bu nedenle Doğru Cevap A seçeneği olur.
4.Soru
kısıtı altında f(x,y)=xy fonksiyonunu optimize eden (x,y) ikilisi aşağıdakilerden hangisidir?
|
(6,6) |
|
(2,3) |
|
(3,2) |
|
(3,3) |
|
(6,0) |
Yerine koyma metodu ve sonrasında 1. derece kısmi türev koşullarını uygulayalım uygulayalım:
bu durumda (x,y) ikilisi (3,2) olacaktır
5.Soru
Kırmızı et için talep ve arz fonksiyonları sırasıyla
Qd=-8P+1000
Qs=5P-200
Şeklindedir. Kırmızı et piyasası dengedeyken hükümet sağlıklı beslenmeyi teşvik etmek için satılan her kilo et için t=20 TL lik vergi koymuş ve bu vergiyi de et satıcılarına yüklemiştir. Vergi sonrası piyasada gerçekleşen denge fiyatı aşağıdakilerden hangisidir?
|
50 |
|
80 |
|
90 |
|
100 |
|
125 |
Verginin satıcılara yüklenmesi durumunda p piyasa fiyatından ürününü satan satıcı, t lira kadar vergiyi devlete ödemek zorundadır. Bu yüzden sattığı her birimden piyasa fiyatı olan p değil de p-t alır.
Bu durumda vergi sonrası yeni arz fonksiyonu
Qs=5(p-20)-200 olur. Qs=5P-100-200 Qs=5P-300
Talep fonksiyonu değişmez. Qd=-8P+1000
Denge koşulu Qs=Qd
5P-300=-8P+1000
13P=1300
P=100 olarak hesaplanır.
6.Soru
Aşağıda ikinci dereceden koşullar ile ilgili verilen ifadelerden hangisi yanlıştır?
|
Amaç fonksiyonunun maksimumda mı yoksa minimumda mı olduğunu belirlemek için ikinci dereceden koşulların incelenmesi gerekir. |
|
Sınırlandırılmış Hessian matrisi amaç fonksiyonunun maksimum mu yoksa minimum mu olduğunu belirlemek için oluşturulur. |
|
Sınırlandırılmış Hessian matrisi ikinci derecede türevlerden oluşan Hessian matrisin, kısıt fonksiyonunun birinci dereceden türevleri ile sınırlandırılmış halidir. |
|
Sınırlandırılmış Hessian’ın bütün asal minörleri negatifse amaç fonksiyonu minimumdadır. |
|
Sınırlandırılmış Hessian’ın asal minörleri pozitiften başlayarak işaret değiştiriyorsa amaç fonksiyonu minimumdadır. |
Amaç fonksiyonunun minimumda mı yoksa maksimumda mı olduğunu belirlemek için ikinci dereceden koşulların incelenmesi gerek. Bunun için sınırlandırılmış Hessian matrisi oluşturulur ve matrisin pozitif mi yoksa negatif mi olduğu araştırılır. Eğer sınırlandırılmış Hessian’ın bütün asal minörleri negatifse amaç fonksiyonu minimumda, asal minörler pozitiften başlayarak işaret değiştiriyorsa amaç fonksiyonu maksimumdadır. Dolayısıyla E seçeneğinde ikinci dereceden koşullar ile ilgili verilen ifade hatalı bir ifadedir.
7.Soru
Verilen matrisin determinantı aşağıdakilerden hangisidir?
|
45 |
|
-56 |
|
-82 |
|
20 |
|
-78 |
8.Soru
Soruda verilenlere göre çarpan değeri aşağıdakilerden hangisidir?
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
9.Soru
Eş-ürün eğrisi 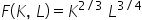 olarak veriliyor. Buna göre marjinal teknik ikame oranı aşağıdakilerden hangisidir?
olarak veriliyor. Buna göre marjinal teknik ikame oranı aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
|
Marjinal teknik ikâme oranını bulmak için eş-ürün eğrisi kapalı fonksiyonunun türevini almamız gerekmektedir. Buradan ilgili kısmi türevler
olarak elde edilir. Bu eşitlikler kapalı fonksiyonun türevinde yerine konulduğunda
olarak elde edilir. Dolayısıyla Doğru Cevap B seçeneği olur.
10.Soru
Bir A matrisinin tersi 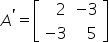 biçiminde veriliyor. Buna göre A matrisi aşağıdakilerden hangisidir?
biçiminde veriliyor. Buna göre A matrisi aşağıdakilerden hangisidir?
|
|
|
|
|
|
|
|
|
|
Bir matrisin tersinin tersi kendisine eşittir. Bu noktadan hareketle soruda A matrisinin tersi verildiğinden A matrisinin tersine yine ters alma işlemi uyguladığımızda A matrisinin kendisini elde etmiş oluruz. O halde,
matrisinin tersi;
eşitliği yardımıyla bulunur. Buradan Ek (A') matrisi
olarak elde edilir. A' matrisinin determinantı ise;
olarak bulunur. Bu elde edilenlere göre A' matrisinin tersine
biçiminde ulaşılmış olur. Bu nedenle Doğru Cevap C seçeneğidir.
11.Soru
Fayda fonksiyonu biçiminde olan bir tüketici x malını 5 TL ve y malını 2 TL den satın almaktadır. Bu iki mal için harcayabileceği toplam 150 TL si olan bu tüketicinin faydasını maksimize etmek için ne kadar y tüketmelidir?
|
5 |
|
12 |
|
24 |
|
36 |
|
50 |
y=5x=5.10=50
12.Soru
I. Tüketicinin Fayda Maksimizasyonu
II. Tüketicinin Harcama Minimizasyonu
III. Maliyet Maksimizasyonu
IV. Üretim Maksimizasyonu
Verilenlerden hangileri kısıtlı optimizasyonun iktisadi uygulamaları arasına girer?
|
I ve II |
|
I, II ve III |
|
I, II ve IV |
|
I, III ve IV |
|
Hepsi |
Kısıtlı optimizasyonun iktisadi uygulamaları arasında tüketicinin fayda maksimizasyonu, tüketicinin harcama minimizasyonu, maliyet minimizasyonu ve üretim maksimizasyonu vardır. Maliyet maksimizasyonu yoktur. I, II ve IV önermeleri kısıtlı optimizasyonun iktisadi uygulamaları arasında bulunur.
13.Soru
Üç mal üreten bir firmanın kâr fonksiyonu
(Q1,Q2,Q3) = TR(Q1)+TR(Q2)+TR(Q3) - TC (Q1,Q2,Q3) olarak verilmiştir. Bu fonksiyonun birinci mertebeden türevleri sıfıra eşitlenerek bulunan denklemler eşanlı olarak çözülmüş ve miktarları elde edilmiştir. İkinci mertebeden türevi alınarak oluşturulan Hessian matrisinin asal minörleri |H|1 ,|H|2 ve |H|3 ’tür. Bu firmanın kârını maksimum yapıp yapmadığına karar verebilmek için asal minörlerin işaretleri aşağıdakilerden hangisi olmalıdır?
|
|H1|<0,|H2|<0,|H3 |<0 |
|
|H1|<0,|H2|>0,|H3 |<0 |
|
|H1|>0,|H2|>0,|H3|>0 |
|
|H1|<0,|H2|>0,|H3|>0 |
|
|H1|>0,|H2|<0,|H3|<0 |
Asal minörler, |H1|<0,|H2|>0,|H3 |<0
ise Hessian matrisi negatif belirlidir. Bu durumda (Q1,Q2,Q3) değerlerinin amaç fonksiyonunu maksimum kılan değerler olduğu söylenir.
14.Soru
4x2+ 2xy + 7y2 amaç fonksiyonunu g (x, y) = x + y = 90 kısıtı altında Lagrange çarpanı aşağıdakilerden hangisidir?
|
0 |
|
360 |
|
480 |
|
540 |
|
900 |
Bu optimizasyon problemini çözmek için öncelikle kısıt fonksiyonunu sıfıra eşitleyip sonra Lagrange fonksiyonu oluşturmalıyız. Lagrange fonksiyonu L(x, y, ?) = 4x2 + 2xy + 7y2 + ? (90 - x - y) şeklinde yazılır. Her bir değişken için I. derecen kısmi türevleri alarak, birinci dereceden koşulları yazdığımızda x için birinci türev 8x + 2y – ? = 0, y için birinci türev 2x + 14y – ? = 0 ve ? için birinci türev 90 - x – y = 0 buradan ?=8x + 2y = 2x + 14y eşitliğini buluruz. Bu ifadede x ve y’leri aynı tarafa toplarsak 6x = 12y ifadesini buluruz.
Buradan da x=2y ifadesini buluruz. Bulduğumuz x ya da y ifadesini 90 - x – y = 0 yerine yazarız. 90 – 2y -y = 0 bu ifade 90 – 3y=0 şeklinde yazılır. Buradan y = 30 ve x =60 buluruz. Lagrange çarpanı ?=8x + 2y = 2x + 14y eşitliklerinden herhangi birinden bulunabilir. ?=8*(60) + 2*(30) =540
15.Soru
Marjinal tüketim eğiliminin (MPC) değeri 0,75 ise marjinal tasarruf eğiliminin (MPS) değeri aşağıdakilerden hangisidir?
|
0,10 |
|
0,15 |
|
0,20 |
|
0,25 |
|
0,30 |
MPC+MPS=1 olur
Bu nedenle MPC=0,75 olarak verildiğinden
MPS=1-0,75=0,25 olur.
16.Soru
Toplam hasıla fonksiyonu 8Q – 5Q2 ve toplam maliyet fonksiyonu 3Q2 + 4Q - 12 olduğuna göre firmanın kârını maksimum yapan üretim düzeyinde toplam hasıla kaçtır?
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
Kâr fonksiyonu toplam hasıladan toplam maliyetin farkı ile bulunur. π= 8Q – 5Q2 – (3Q2 + 4Q – 12) = 8Q – 5Q2 + 3Q2 - 4Q + 12 bu ifadeyi düzenlediğimizde π= -2Q2 + 4Q +12 ifadesini elde ederiz. Kâr fonksiyonunun türevini aldığımız zaman ise – 4Q +4 ifadesini buluruz. Bu ifadeyi sıfıra eşitlediğimiz zaman kârın maksimum olduğu üretim düzeyini buluruz. – 4Q +4=0 buradan Q = 1 olduğunu buluruz. Toplam hasılayı bulabilmek için bu Q değerini toplam hâsıla fonksiyonuna yazmamız gerekir. Toplam hâsıla fonksiyonundan TR(1)= 8Q – 5Q2= 8-5*1=3 sonucunu buluruz.
17.Soru
Matrislerle ilgili aşağıda verilen tanımlardan hangisi doğru verilmiştir?
|
Simetrik matris: Satır ve sütun sayısı birbirine eşit olan matristir. |
|
Köşegen matris: Köşegen elemanları bir olan skaler matristir. |
|
Birim matris: Köşegeninin alt veya üstündeki elemanları sıfırdan oluşan kare matristir. |
|
Vektör: Tek bir satır veya sütundan oluşan matristir. |
|
Kare matris: Sadece köşegen elemanları sıfır olmayan matristir. |
Kare matris: Satır ve sütun sayısı birbirine eşit olan matristir. Birim matris: Köşegen elemanları bir olan skaler matristir. Üçgensel matris: Köşegeninin alt veya üstündeki elemanları sıfırdan oluşan kare matristir. Vektör: Tek bir satır veya sütundan oluşan matristir. Köşegen matris: Sadece köşegen elemanları sıfır olmayan matristir. Simetrik matris: Tüm i ve j’ler için, aij = aji koşulu gerçekleşen matristir.
18.Soru
U(x,y)=4xy şeklinde yanlız x ve y mallarını tüketen Ahmet'in fayda fonnksiyonu verilmiştir. Ahmet 1 br. x için 3 TL. ve 1 br. y için 5 TL ödemektedir. Bu iki malı tüketmek için Ahmet'in toplam 300 TL. si bulunmaktadır. Buna göre Ahmet maksimum fayda elde edebilmek için ne kadar x tüketmelidir?
|
10 |
|
20 |
|
30 |
|
40 |
|
50 |
19.Soru
Aşağıdakilerden hangisi önce K’ya sonra L’ye göre türevi 4L olan fonksiyondur?
|
2LK
|
|
KL2
|
|
2KL2
|
|
LK4
|
|
L2K4
|
-
- 1.SORU ÇÖZÜLMEDİ
- 2.SORU ÇÖZÜLMEDİ
- 3.SORU ÇÖZÜLMEDİ
- 4.SORU ÇÖZÜLMEDİ
- 5.SORU ÇÖZÜLMEDİ
- 6.SORU ÇÖZÜLMEDİ
- 7.SORU ÇÖZÜLMEDİ
- 8.SORU ÇÖZÜLMEDİ
- 9.SORU ÇÖZÜLMEDİ
- 10.SORU ÇÖZÜLMEDİ
- 11.SORU ÇÖZÜLMEDİ
- 12.SORU ÇÖZÜLMEDİ
- 13.SORU ÇÖZÜLMEDİ
- 14.SORU ÇÖZÜLMEDİ
- 15.SORU ÇÖZÜLMEDİ
- 16.SORU ÇÖZÜLMEDİ
- 17.SORU ÇÖZÜLMEDİ
- 18.SORU ÇÖZÜLMEDİ
- 19.SORU ÇÖZÜLMEDİ


